Question Number 64333 by Chi Mes Try last updated on 16/Jul/19
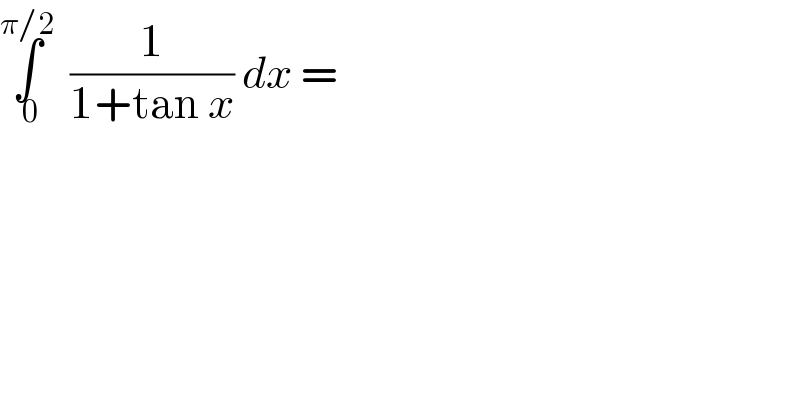
$$\underset{\:\mathrm{0}} {\overset{\pi/\mathrm{2}} {\int}}\:\:\frac{\mathrm{1}}{\mathrm{1}+\mathrm{tan}\:{x}}\:{dx}\:= \\ $$
Commented by mathmax by abdo last updated on 16/Jul/19
![let I =∫_0 ^(π/2) (dx/(1+tanx)) changement tanx =t give I =∫_0 ^(+∞) (dt/((1+t^2 )(1+t))) let decompose F(t)=(1/((t+1)(t^2 +1))) F(t)=(a/(t+1)) +((bt+c)/(t^2 +1)) a=lim_(t→−1) (t+1)F(t) =(1/2) lim_(t→+∞) tF(t) =0 =a+b ⇒b=−(1/2) ⇒F(t) =(1/(2(t+1))) +((−(1/2)t +c)/(t^2 +1)) F(0)=1 =(1/2) +c ⇒c=(1/2) ⇒F(t) =(1/(2(t+1))) −(1/2) ((t−1)/(t^2 +1)) ⇒ I =∫_0 ^∞ ((1/(2(t+1)))−(1/4)((2t)/(t^2 +1)))dt +(1/2)∫_0 ^∞ (dt/(t^2 +1)) =(1/2)[ln∣t+1∣−(1/2)ln(t^2 +1)]_0 ^(+∞) +(π/4) =(1/2)[ln∣((t+1)/( (√(t^2 +1))))∣]_0 ^(+∞) +(π/4) =0 +(π/4) ⇒ I =(π/4) .](https://www.tinkutara.com/question/Q64343.png)
$${let}\:{I}\:=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:\:\frac{{dx}}{\mathrm{1}+{tanx}}\:{changement}\:{tanx}\:={t}\:{give} \\ $$$${I}\:=\int_{\mathrm{0}} ^{+\infty} \:\:\:\frac{{dt}}{\left(\mathrm{1}+{t}^{\mathrm{2}} \right)\left(\mathrm{1}+{t}\right)}\:\:{let}\:{decompose}\:{F}\left({t}\right)=\frac{\mathrm{1}}{\left({t}+\mathrm{1}\right)\left({t}^{\mathrm{2}} \:+\mathrm{1}\right)} \\ $$$${F}\left({t}\right)=\frac{{a}}{{t}+\mathrm{1}}\:+\frac{{bt}+{c}}{{t}^{\mathrm{2}} \:+\mathrm{1}} \\ $$$${a}={lim}_{{t}\rightarrow−\mathrm{1}} \left({t}+\mathrm{1}\right){F}\left({t}\right)\:=\frac{\mathrm{1}}{\mathrm{2}} \\ $$$${lim}_{{t}\rightarrow+\infty} \:{tF}\left({t}\right)\:=\mathrm{0}\:={a}+{b}\:\Rightarrow{b}=−\frac{\mathrm{1}}{\mathrm{2}}\:\Rightarrow{F}\left({t}\right)\:=\frac{\mathrm{1}}{\mathrm{2}\left({t}+\mathrm{1}\right)}\:+\frac{−\frac{\mathrm{1}}{\mathrm{2}}{t}\:+{c}}{{t}^{\mathrm{2}} \:+\mathrm{1}} \\ $$$${F}\left(\mathrm{0}\right)=\mathrm{1}\:=\frac{\mathrm{1}}{\mathrm{2}}\:+{c}\:\Rightarrow{c}=\frac{\mathrm{1}}{\mathrm{2}}\:\Rightarrow{F}\left({t}\right)\:=\frac{\mathrm{1}}{\mathrm{2}\left({t}+\mathrm{1}\right)}\:−\frac{\mathrm{1}}{\mathrm{2}}\:\frac{{t}−\mathrm{1}}{{t}^{\mathrm{2}} \:+\mathrm{1}}\:\Rightarrow \\ $$$${I}\:=\int_{\mathrm{0}} ^{\infty} \left(\frac{\mathrm{1}}{\mathrm{2}\left({t}+\mathrm{1}\right)}−\frac{\mathrm{1}}{\mathrm{4}}\frac{\mathrm{2}{t}}{{t}^{\mathrm{2}} \:+\mathrm{1}}\right){dt}\:+\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\infty} \:\frac{{dt}}{{t}^{\mathrm{2}} \:+\mathrm{1}} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\left[{ln}\mid{t}+\mathrm{1}\mid−\frac{\mathrm{1}}{\mathrm{2}}{ln}\left({t}^{\mathrm{2}} \:+\mathrm{1}\right)\right]_{\mathrm{0}} ^{+\infty} \:+\frac{\pi}{\mathrm{4}} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\left[{ln}\mid\frac{{t}+\mathrm{1}}{\:\sqrt{{t}^{\mathrm{2}} \:+\mathrm{1}}}\mid\right]_{\mathrm{0}} ^{+\infty} \:+\frac{\pi}{\mathrm{4}}\:=\mathrm{0}\:+\frac{\pi}{\mathrm{4}}\:\Rightarrow\:{I}\:=\frac{\pi}{\mathrm{4}}\:. \\ $$$$ \\ $$
Commented by Tony Lin last updated on 17/Jul/19

$$\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \frac{\mathrm{1}}{\mathrm{1}+{tanx}}{dx} \\ $$$$=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \frac{{cosx}}{{cosx}+{sinx}}{dx} \\ $$$$=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \frac{{cos}\left({cosx}−{sinx}\right)}{\left({cosx}+{sinx}\right)\left({cosx}−{sinx}\right)}{dx} \\ $$$$=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \frac{{cos}^{\mathrm{2}} {x}−{cosxsinx}}{{cos}^{\mathrm{2}} {x}−{sin}^{\mathrm{2}} {x}}{dx} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \frac{{cos}\mathrm{2}{x}+\mathrm{1}−{sin}\mathrm{2}{x}}{{cos}\mathrm{2}{x}}{dx} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} {dx}−\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} {tan}\mathrm{2}{xdx}+\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} {sec}\mathrm{2}{xdx} \\ $$$$=\frac{\pi}{\mathrm{4}} \\ $$
Answered by Rio Michael last updated on 16/Jul/19

$${begin}\:{with} \\ $$$$\int\frac{\mathrm{1}}{\mathrm{1}+{tanx}}{dx} \\ $$$${I}\:=\:\int\frac{\mathrm{1}}{\mathrm{1}+{tanx}}{dx}\:\:\:\:\:\:{use}\:{the}\:{substitution}\:{u}\:=\:{tanx} \\ $$$${I}\:=\:\int\frac{\mathrm{1}}{\left(\mathrm{1}+{u}^{\mathrm{2}} \right)\left(\mathrm{1}+{u}\right)}{du} \\ $$$${I}\:=\:\frac{\mathrm{1}}{\mathrm{2}}\int\left(\frac{\mathrm{1}}{\mathrm{1}+{u}^{\mathrm{2}} }\:+\:\frac{\mathrm{1}}{\mathrm{1}+{u}}\right){du} \\ $$$${I}\:=\:\frac{\mathrm{1}}{\mathrm{2}}\int\left(\frac{\mathrm{1}}{\mathrm{1}+{u}^{\mathrm{2}} }−\frac{\mathrm{1}}{\mathrm{2}}\:\frac{\mathrm{2}{u}}{\mathrm{1}+{u}^{\mathrm{2}} }\:+\:\frac{\mathrm{1}}{\mathrm{1}+{u}}\right){du} \\ $$$${I}\:=\:\frac{\mathrm{1}}{\mathrm{2}}\left({arctanu}−\frac{\mathrm{1}}{\mathrm{2}}{ln}\left(\mathrm{1}+{u}^{\mathrm{2}} \right)+{ln}\left(\mathrm{1}+{u}\right)\right) \\ $$$${I}\:=\:\lceil\:\frac{\mathrm{1}}{\mathrm{2}}\left({x}−{ln}\left({secx}\right)\:+\:{ln}\left(\mathrm{1}+{tanx}\right)\right)\rceil_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \\ $$$${I}\:=\:\frac{\mathrm{1}}{\mathrm{2}}\left(\frac{\pi}{\mathrm{2}}+{ln}\left({sin}\frac{\pi}{\mathrm{2}}+{cos}\frac{\pi}{\mathrm{2}}\right)\right)\:=\:\frac{\pi}{\mathrm{4}} \\ $$$$ \\ $$
Answered by Tanmay chaudhury last updated on 17/Jul/19
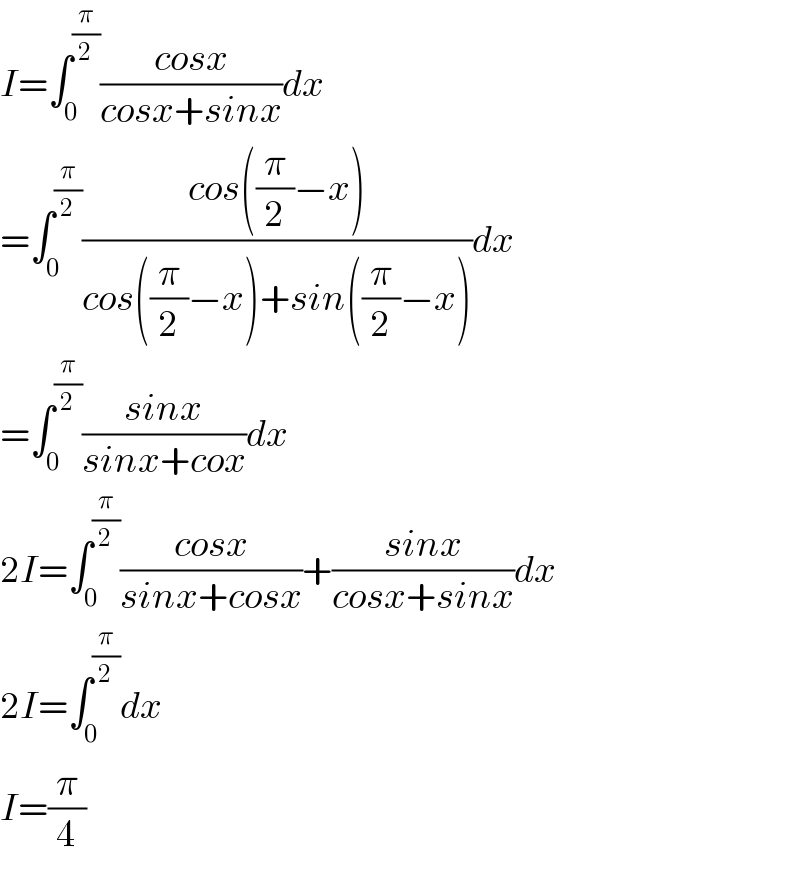
$${I}=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \frac{{cosx}}{{cosx}+{sinx}}{dx} \\ $$$$=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \frac{{cos}\left(\frac{\pi}{\mathrm{2}}−{x}\right)}{{cos}\left(\frac{\pi}{\mathrm{2}}−{x}\right)+{sin}\left(\frac{\pi}{\mathrm{2}}−{x}\right)}{dx} \\ $$$$=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \frac{{sinx}}{{sinx}+{cox}}{dx} \\ $$$$\mathrm{2}{I}=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \frac{{cosx}}{{sinx}+{cosx}}+\frac{{sinx}}{{cosx}+{sinx}}{dx} \\ $$$$\mathrm{2}{I}=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} {dx} \\ $$$${I}=\frac{\pi}{\mathrm{4}} \\ $$
