Question Number 137829 by mnjuly1970 last updated on 07/Apr/21
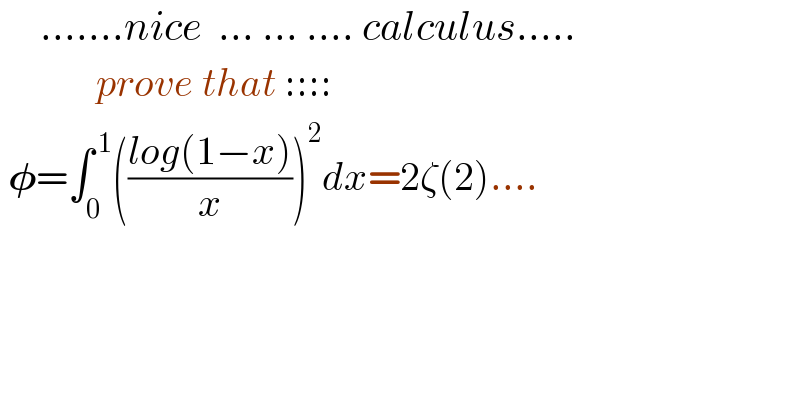
$$\:\:\:\:\:…….{nice}\:\:…\:…\:….\:{calculus}….. \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:{prove}\:{that}\::::: \\ $$$$\:\boldsymbol{\phi}=\int_{\mathrm{0}} ^{\:\mathrm{1}} \left(\frac{{log}\left(\mathrm{1}β{x}\right)}{{x}}\right)^{\mathrm{2}} {dx}=\mathrm{2}\zeta\left(\mathrm{2}\right)…. \\ $$$$ \\ $$
Answered by EnterUsername last updated on 07/Apr/21
![β«_0 ^1 (((ln(1βx))/x))^2 dx =β«_0 ^1 ((ln^2 x)/((1βx)^2 ))dx=[((ln^2 x)/(1βx))β2β«((lnx)/(x(1βx)))dx]_0 ^1 =[((ln^2 x)/(1βx))β2β«(((lnx)/x)+((lnx)/(1βx)))dx]_0 ^1 =[((ln^2 x)/(1βx))βln^2 x]_0 ^1 β2β«_0 ^1 ((lnx)/(1βx))dx =2Οβ²(1)=2Ξ£_(n=0) ^β (1/((n+1)^2 ))=2Ξ£_(n=1) ^β (1/n^2 )=2ΞΆ(2)=(Ο^2 /3)](https://www.tinkutara.com/question/Q137831.png)
$$\int_{\mathrm{0}} ^{\mathrm{1}} \left(\frac{{ln}\left(\mathrm{1}β{x}\right)}{{x}}\right)^{\mathrm{2}} {dx} \\ $$$$=\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{ln}^{\mathrm{2}} {x}}{\left(\mathrm{1}β{x}\right)^{\mathrm{2}} }{dx}=\left[\frac{{ln}^{\mathrm{2}} {x}}{\mathrm{1}β{x}}β\mathrm{2}\int\frac{{lnx}}{{x}\left(\mathrm{1}β{x}\right)}{dx}\right]_{\mathrm{0}} ^{\mathrm{1}} \\ $$$$=\left[\frac{{ln}^{\mathrm{2}} {x}}{\mathrm{1}β{x}}β\mathrm{2}\int\left(\frac{{lnx}}{{x}}+\frac{{lnx}}{\mathrm{1}β{x}}\right){dx}\right]_{\mathrm{0}} ^{\mathrm{1}} \\ $$$$=\left[\frac{{ln}^{\mathrm{2}} {x}}{\mathrm{1}β{x}}β{ln}^{\mathrm{2}} {x}\right]_{\mathrm{0}} ^{\mathrm{1}} β\mathrm{2}\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{lnx}}{\mathrm{1}β{x}}{dx} \\ $$$$=\mathrm{2}\psi'\left(\mathrm{1}\right)=\mathrm{2}\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{\left({n}+\mathrm{1}\right)^{\mathrm{2}} }=\mathrm{2}\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{{n}^{\mathrm{2}} }=\mathrm{2}\zeta\left(\mathrm{2}\right)=\frac{\pi^{\mathrm{2}} }{\mathrm{3}} \\ $$
Commented by mnjuly1970 last updated on 07/Apr/21
$${thanks}\:{alot}\:… \\ $$