Question Number 137963 by floor(10²Eta[1]) last updated on 08/Apr/21
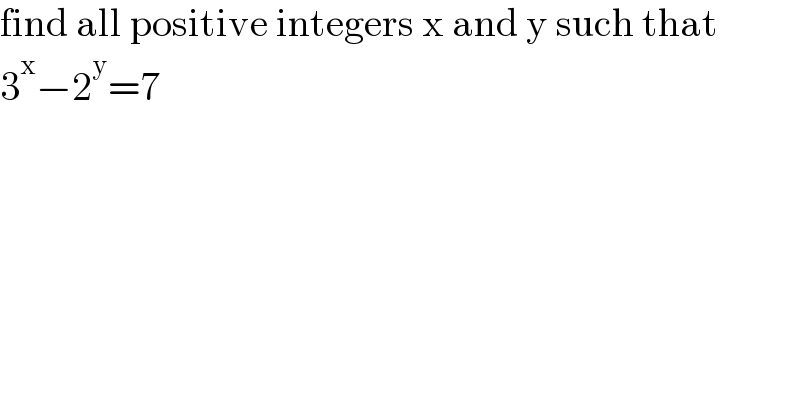
$$\mathrm{find}\:\mathrm{all}\:\mathrm{positive}\:\mathrm{integers}\:\mathrm{x}\:\mathrm{and}\:\mathrm{y}\:\mathrm{such}\:\mathrm{that} \\ $$$$\mathrm{3}^{\mathrm{x}} −\mathrm{2}^{\mathrm{y}} =\mathrm{7} \\ $$
Commented by PRITHWISH SEN 2 last updated on 08/Apr/21

$$\boldsymbol{\mathrm{x}}=\mathrm{2},\:\boldsymbol{\mathrm{y}}=\mathrm{1} \\ $$
Answered by mindispower last updated on 08/Apr/21
![3^x =7+2^y by using modd[8] 3^(2k+1) ≡3[8] 3^(2k) ≡1[9]⇒3^x ≡{1,3}[8]....1 if y≥3⇒2^y +7≡7[8]...2 (1)&(2)⇒no sulution⇒y≤2 y=0⇒3^x =8⇒x∈R−Z y=1⇒3^x =9⇒x=2 y=2⇒3^x =11⇒x∈R−Z (x^� ,y)=(2,1)](https://www.tinkutara.com/question/Q137968.png)
$$\mathrm{3}^{{x}} =\mathrm{7}+\mathrm{2}^{{y}} \\ $$$${by}\:{using}\:{modd}\left[\mathrm{8}\right] \\ $$$$\mathrm{3}^{\mathrm{2}{k}+\mathrm{1}} \equiv\mathrm{3}\left[\mathrm{8}\right] \\ $$$$\mathrm{3}^{\mathrm{2}{k}} \equiv\mathrm{1}\left[\mathrm{9}\right]\Rightarrow\mathrm{3}^{{x}} \equiv\left\{\mathrm{1},\mathrm{3}\right\}\left[\mathrm{8}\right]….\mathrm{1} \\ $$$${if}\:{y}\geqslant\mathrm{3}\Rightarrow\mathrm{2}^{{y}} +\mathrm{7}\equiv\mathrm{7}\left[\mathrm{8}\right]…\mathrm{2} \\ $$$$\left(\mathrm{1}\right)\&\left(\mathrm{2}\right)\Rightarrow{no}\:{sulution}\Rightarrow{y}\leqslant\mathrm{2} \\ $$$${y}=\mathrm{0}\Rightarrow\mathrm{3}^{{x}} =\mathrm{8}\Rightarrow{x}\in\mathbb{R}−\mathbb{Z} \\ $$$${y}=\mathrm{1}\Rightarrow\mathrm{3}^{{x}} =\mathrm{9}\Rightarrow{x}=\mathrm{2} \\ $$$${y}=\mathrm{2}\Rightarrow\mathrm{3}^{{x}} =\mathrm{11}\Rightarrow{x}\in\mathbb{R}−\mathbb{Z} \\ $$$$\left(\bar {{x}},{y}\right)=\left(\mathrm{2},\mathrm{1}\right) \\ $$
