Question Number 137973 by mnjuly1970 last updated on 08/Apr/21
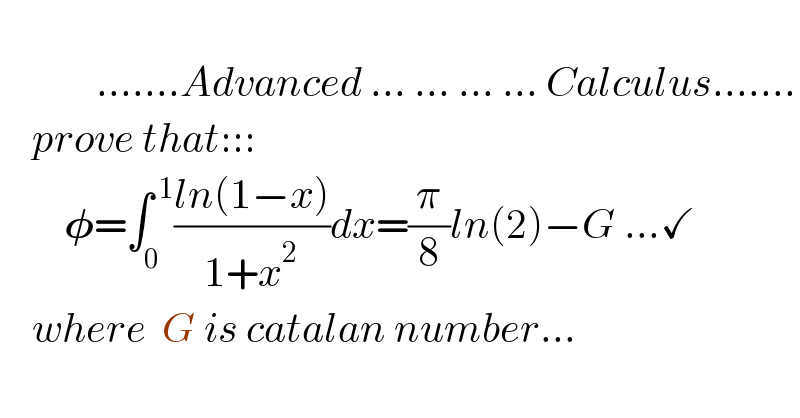
$$\:\:\:\:\:\:\:\:\: \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:…….{Advanced}\:…\:…\:…\:…\:{Calculus}……. \\ $$$$\:\:\:\:{prove}\:{that}::: \\ $$$$\:\:\:\:\:\:\:\:\boldsymbol{\phi}=\int_{\mathrm{0}} ^{\:\mathrm{1}} \frac{{ln}\left(\mathrm{1}β{x}\right)}{\mathrm{1}+{x}^{\mathrm{2}} }{dx}=\frac{\pi}{\mathrm{8}}{ln}\left(\mathrm{2}\right)β{G}\:…\checkmark \\ $$$$\:\:\:\:{where}\:\:{G}\:{is}\:{catalan}\:{number}… \\ $$$$\:\:\: \\ $$
Answered by EnterUsername last updated on 08/Apr/21
![β«_0 ^1 ((ln(1βx))/(1+x^2 ))dx=β«_0 ^(Ο/4) ln(1βtanΞΈ)dΞΈ =β«_0 ^(Ο/4) ln(cosxβsinx)dxββ«_0 ^(Ο/4) lncosxdx =β«_0 ^(Ο/4) ln[(β2)cos(x+(Ο/4))]dxβ((G/2)β((Οln2)/4)) =(Ο/8)ln2+β«_0 ^(Ο/4) ln(sinx)dxβ((G/2)β((Οln2)/4)) =(Ο/8)ln2β(G/2)β((Οln2)/4)β((G/2)β((Οln2)/4))=(Ο/8)ln2βG](https://www.tinkutara.com/question/Q137975.png)
$$\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{ln}\left(\mathrm{1}β{x}\right)}{\mathrm{1}+{x}^{\mathrm{2}} }{dx}=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} {ln}\left(\mathrm{1}β{tan}\theta\right){d}\theta \\ $$$$=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} {ln}\left({cosx}β{sinx}\right){dx}β\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} {lncosxdx} \\ $$$$=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} {ln}\left[\sqrt{\mathrm{2}}{cos}\left({x}+\frac{\pi}{\mathrm{4}}\right)\right]{dx}β\left(\frac{{G}}{\mathrm{2}}β\frac{\pi{ln}\mathrm{2}}{\mathrm{4}}\right) \\ $$$$=\frac{\pi}{\mathrm{8}}{ln}\mathrm{2}+\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} {ln}\left({sinx}\right){dx}β\left(\frac{{G}}{\mathrm{2}}β\frac{\pi{ln}\mathrm{2}}{\mathrm{4}}\right) \\ $$$$=\frac{\pi}{\mathrm{8}}{ln}\mathrm{2}β\frac{{G}}{\mathrm{2}}β\frac{\pi{ln}\mathrm{2}}{\mathrm{4}}β\left(\frac{{G}}{\mathrm{2}}β\frac{\pi{ln}\mathrm{2}}{\mathrm{4}}\right)=\frac{\pi}{\mathrm{8}}{ln}\mathrm{2}β{G} \\ $$
Commented by mnjuly1970 last updated on 08/Apr/21
$$\:{grateful}… \\ $$
Answered by mathmax by abdo last updated on 09/Apr/21
![f(a)=β«_0 ^1 ((ln(1+ax))/(1+x^2 ))dx βf^β² (a)=β«_0 ^1 (x/((ax+1)(x^2 +1)))dx =(1/a)β«_0 ^1 ((ax+1β1)/((ax+1)(x^2 +1)))dx =(1/a)[arctanx]_0 ^1 β(1/a)β«_0 ^1 (dx/((ax+1)(x^2 +1))) =(Ο/(4a))β(1/a)β«_0 ^1 (dx/((ax+1)(x^2 +1))) let decompose F(x)=(1/((ax+1)(x^2 +1))) F(x)=(Ξ±/(ax+1)) +((mx+n)/(x^2 +1)) Ξ±=(1/((1/a^2 )+1)) =(a^2 /(1+a^2 )) lim_(xβ+β) xF(x)=0=(Ξ±/a) +m βm=β(a/(1+a^2 )) F(o)=1=Ξ±+n βn=1β(a^2 /(1+a^2 ))=(1/(1+a^2 )) βF(x)=(a^2 /((a^2 +1)(ax+1))) +((β(a/(a^2 +1))x+(1/(1+a^2 )))/(x^2 +1)) ββ«_0 ^1 F(x)dx=(a^2 /(a^2 +1))β«_0 ^1 (dx/(ax+1)) β(1/(a^2 +1))β«_0 ^1 ((axβ1)/(x^2 +1))dx =(a/(a^2 +1))[ln(ax+1)]_0 ^1 β(a/(2(a^2 +1)))β«_0 ^1 ((2x)/(x^2 +1))dx +(Ο/(4(a^2 +1)))=((aln(a+1))/(a^2 +1)) β(a/(2(a^2 +1)))ln(2)+(Ο/(4(a^2 +1))) β f^β² (a)=(Ο/(4a))β((ln(a+1))/(a^2 +1))+((ln2)/(2(a^2 +1))) β(Ο/(4a(a^2 +1))) =(Ο/(4a))(1β(1/(a^2 +1)))β((ln(a+1))/(a^2 +1))+((ln2)/(2(a^2 +1))) =((Οa)/4)β((ln(a+1))/(a^2 +1))+((ln2)/(2(a^2 +1))) ββ«_0 ^1 f^β² (a)da =(Ο/4)β«_0 ^1 ada ββ«_0 ^1 ((ln(a+1))/(a^2 +1))da+((ln2)/2)β«_0 ^1 (da/(a^2 +1)) =(Ο/4)Γ(1/2) ββ«_0 ^1 ((ln(1+x))/(x^2 +1))dx +((ln2)/2).(Ο/4) =(Ο/8)ββ«_0 ^1 ((ln(1+x))/(x^2 +1))dx+(Ο/8)ln2 =f(1)=β«_0 ^1 ((ln(1+x))/(1+x^2 ))dx β 2β«_0 ^1 ((ln(1+x))/(x^2 +1))dx =(Ο/8)+(Ο/8)ln2 ββ«_0 ^1 ((ln(1+x))/(x^2 +1))dx =(Ο/(16))+(Ο/(16))ln2 ? if we want β«_0 ^1 ((ln(1βx))/(x^2 +1))dx we use the parametric f(a)=β«_0 ^1 ((ln(1βax))/(x^2 +1))dx....be continued....](https://www.tinkutara.com/question/Q138002.png)
$$\mathrm{f}\left(\mathrm{a}\right)=\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{\mathrm{ln}\left(\mathrm{1}+\mathrm{ax}\right)}{\mathrm{1}+\mathrm{x}^{\mathrm{2}} }\mathrm{dx}\:\Rightarrow\mathrm{f}^{'} \left(\mathrm{a}\right)=\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{\mathrm{x}}{\left(\mathrm{ax}+\mathrm{1}\right)\left(\mathrm{x}^{\mathrm{2}} \:+\mathrm{1}\right)}\mathrm{dx} \\ $$$$=\frac{\mathrm{1}}{\mathrm{a}}\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{\mathrm{ax}+\mathrm{1}β\mathrm{1}}{\left(\mathrm{ax}+\mathrm{1}\right)\left(\mathrm{x}^{\mathrm{2}} \:+\mathrm{1}\right)}\mathrm{dx}\:=\frac{\mathrm{1}}{\mathrm{a}}\left[\mathrm{arctanx}\right]_{\mathrm{0}} ^{\mathrm{1}} β\frac{\mathrm{1}}{\mathrm{a}}\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{\mathrm{dx}}{\left(\mathrm{ax}+\mathrm{1}\right)\left(\mathrm{x}^{\mathrm{2}} \:+\mathrm{1}\right)} \\ $$$$=\frac{\pi}{\mathrm{4a}}β\frac{\mathrm{1}}{\mathrm{a}}\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{\mathrm{dx}}{\left(\mathrm{ax}+\mathrm{1}\right)\left(\mathrm{x}^{\mathrm{2}} \:+\mathrm{1}\right)}\:\:\mathrm{let}\:\mathrm{decompose}\:\mathrm{F}\left(\mathrm{x}\right)=\frac{\mathrm{1}}{\left(\mathrm{ax}+\mathrm{1}\right)\left(\mathrm{x}^{\mathrm{2}} \:+\mathrm{1}\right)} \\ $$$$\mathrm{F}\left(\mathrm{x}\right)=\frac{\alpha}{\mathrm{ax}+\mathrm{1}}\:+\frac{\mathrm{mx}+\mathrm{n}}{\mathrm{x}^{\mathrm{2}} \:+\mathrm{1}} \\ $$$$\alpha=\frac{\mathrm{1}}{\frac{\mathrm{1}}{\mathrm{a}^{\mathrm{2}} }+\mathrm{1}}\:=\frac{\mathrm{a}^{\mathrm{2}} }{\mathrm{1}+\mathrm{a}^{\mathrm{2}} } \\ $$$$\mathrm{lim}_{\mathrm{x}\rightarrow+\infty} \mathrm{xF}\left(\mathrm{x}\right)=\mathrm{0}=\frac{\alpha}{\mathrm{a}}\:+\mathrm{m}\:\Rightarrow\mathrm{m}=β\frac{\mathrm{a}}{\mathrm{1}+\mathrm{a}^{\mathrm{2}} } \\ $$$$\mathrm{F}\left(\mathrm{o}\right)=\mathrm{1}=\alpha+\mathrm{n}\:\Rightarrow\mathrm{n}=\mathrm{1}β\frac{\mathrm{a}^{\mathrm{2}} }{\mathrm{1}+\mathrm{a}^{\mathrm{2}} }=\frac{\mathrm{1}}{\mathrm{1}+\mathrm{a}^{\mathrm{2}} }\:\Rightarrow\mathrm{F}\left(\mathrm{x}\right)=\frac{\mathrm{a}^{\mathrm{2}} }{\left(\mathrm{a}^{\mathrm{2}} \:+\mathrm{1}\right)\left(\mathrm{ax}+\mathrm{1}\right)} \\ $$$$+\frac{β\frac{\mathrm{a}}{\mathrm{a}^{\mathrm{2}} \:+\mathrm{1}}\mathrm{x}+\frac{\mathrm{1}}{\mathrm{1}+\mathrm{a}^{\mathrm{2}} }}{\mathrm{x}^{\mathrm{2}} \:+\mathrm{1}}\:\Rightarrow\int_{\mathrm{0}} ^{\mathrm{1}} \:\mathrm{F}\left(\mathrm{x}\right)\mathrm{dx}=\frac{\mathrm{a}^{\mathrm{2}} }{\mathrm{a}^{\mathrm{2}} \:+\mathrm{1}}\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{\mathrm{dx}}{\mathrm{ax}+\mathrm{1}} \\ $$$$β\frac{\mathrm{1}}{\mathrm{a}^{\mathrm{2}} \:+\mathrm{1}}\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{\mathrm{ax}β\mathrm{1}}{\mathrm{x}^{\mathrm{2}} \:+\mathrm{1}}\mathrm{dx}\:=\frac{\mathrm{a}}{\mathrm{a}^{\mathrm{2}} \:+\mathrm{1}}\left[\mathrm{ln}\left(\mathrm{ax}+\mathrm{1}\right)\right]_{\mathrm{0}} ^{\mathrm{1}} β\frac{\mathrm{a}}{\mathrm{2}\left(\mathrm{a}^{\mathrm{2}} \:+\mathrm{1}\right)}\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{\mathrm{2x}}{\mathrm{x}^{\mathrm{2}} \:+\mathrm{1}}\mathrm{dx} \\ $$$$+\frac{\pi}{\mathrm{4}\left(\mathrm{a}^{\mathrm{2}} \:+\mathrm{1}\right)}=\frac{\mathrm{aln}\left(\mathrm{a}+\mathrm{1}\right)}{\mathrm{a}^{\mathrm{2}} \:+\mathrm{1}}\:β\frac{\mathrm{a}}{\mathrm{2}\left(\mathrm{a}^{\mathrm{2}} \:+\mathrm{1}\right)}\mathrm{ln}\left(\mathrm{2}\right)+\frac{\pi}{\mathrm{4}\left(\mathrm{a}^{\mathrm{2}} \:+\mathrm{1}\right)}\:\Rightarrow \\ $$$$\mathrm{f}^{'} \left(\mathrm{a}\right)=\frac{\pi}{\mathrm{4a}}β\frac{\mathrm{ln}\left(\mathrm{a}+\mathrm{1}\right)}{\mathrm{a}^{\mathrm{2}} \:+\mathrm{1}}+\frac{\mathrm{ln2}}{\mathrm{2}\left(\mathrm{a}^{\mathrm{2}} \:+\mathrm{1}\right)}\:β\frac{\pi}{\mathrm{4a}\left(\mathrm{a}^{\mathrm{2}} \:+\mathrm{1}\right)} \\ $$$$=\frac{\pi}{\mathrm{4a}}\left(\mathrm{1}β\frac{\mathrm{1}}{\mathrm{a}^{\mathrm{2}} +\mathrm{1}}\right)β\frac{\mathrm{ln}\left(\mathrm{a}+\mathrm{1}\right)}{\mathrm{a}^{\mathrm{2}} \:+\mathrm{1}}+\frac{\mathrm{ln2}}{\mathrm{2}\left(\mathrm{a}^{\mathrm{2}} \:+\mathrm{1}\right)}\:=\frac{\pi\mathrm{a}}{\mathrm{4}}β\frac{\mathrm{ln}\left(\mathrm{a}+\mathrm{1}\right)}{\mathrm{a}^{\mathrm{2}} \:+\mathrm{1}}+\frac{\mathrm{ln2}}{\mathrm{2}\left(\mathrm{a}^{\mathrm{2}} \:+\mathrm{1}\right)} \\ $$$$\Rightarrow\int_{\mathrm{0}} ^{\mathrm{1}} \:\mathrm{f}^{'} \left(\mathrm{a}\right)\mathrm{da}\:=\frac{\pi}{\mathrm{4}}\int_{\mathrm{0}} ^{\mathrm{1}} \:\mathrm{ada}\:β\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{\mathrm{ln}\left(\mathrm{a}+\mathrm{1}\right)}{\mathrm{a}^{\mathrm{2}} \:+\mathrm{1}}\mathrm{da}+\frac{\mathrm{ln2}}{\mathrm{2}}\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{\mathrm{da}}{\mathrm{a}^{\mathrm{2}} \:+\mathrm{1}} \\ $$$$=\frac{\pi}{\mathrm{4}}Γ\frac{\mathrm{1}}{\mathrm{2}}\:β\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{\mathrm{ln}\left(\mathrm{1}+\mathrm{x}\right)}{\mathrm{x}^{\mathrm{2}} \:+\mathrm{1}}\mathrm{dx}\:+\frac{\mathrm{ln2}}{\mathrm{2}}.\frac{\pi}{\mathrm{4}} \\ $$$$=\frac{\pi}{\mathrm{8}}β\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{\mathrm{ln}\left(\mathrm{1}+\mathrm{x}\right)}{\mathrm{x}^{\mathrm{2}} \:+\mathrm{1}}\mathrm{dx}+\frac{\pi}{\mathrm{8}}\mathrm{ln2}\:\:=\mathrm{f}\left(\mathrm{1}\right)=\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{\mathrm{ln}\left(\mathrm{1}+\mathrm{x}\right)}{\mathrm{1}+\mathrm{x}^{\mathrm{2}} }\mathrm{dx}\:\Rightarrow \\ $$$$\mathrm{2}\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{\mathrm{ln}\left(\mathrm{1}+\mathrm{x}\right)}{\mathrm{x}^{\mathrm{2}} \:+\mathrm{1}}\mathrm{dx}\:=\frac{\pi}{\mathrm{8}}+\frac{\pi}{\mathrm{8}}\mathrm{ln2}\:\Rightarrow\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{\mathrm{ln}\left(\mathrm{1}+\mathrm{x}\right)}{\mathrm{x}^{\mathrm{2}} \:+\mathrm{1}}\mathrm{dx}\:=\frac{\pi}{\mathrm{16}}+\frac{\pi}{\mathrm{16}}\mathrm{ln2}\:\:? \\ $$$$\mathrm{if}\:\mathrm{we}\:\mathrm{want}\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{\mathrm{ln}\left(\mathrm{1}β\boldsymbol{\mathrm{x}}\right)}{\boldsymbol{\mathrm{x}}^{\mathrm{2}} \:+\mathrm{1}}\boldsymbol{\mathrm{dx}}\:\boldsymbol{\mathrm{we}}\:\boldsymbol{\mathrm{use}}\:\boldsymbol{\mathrm{the}}\:\boldsymbol{\mathrm{parametric}} \\ $$$$\boldsymbol{\mathrm{f}}\left(\boldsymbol{\mathrm{a}}\right)=\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{\mathrm{ln}\left(\mathrm{1}β\mathrm{ax}\right)}{\mathrm{x}^{\mathrm{2}} \:+\mathrm{1}}\mathrm{dx}….\mathrm{be}\:\mathrm{continued}…. \\ $$$$ \\ $$