Question Number 7013 by Master Moon last updated on 06/Aug/16
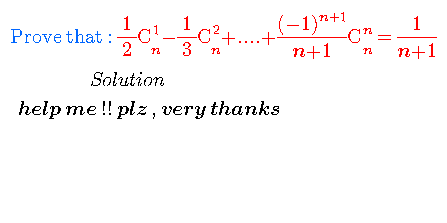
Commented by Yozzis last updated on 06/Aug/16
![(1−x)^n =Σ_(k=0) ^n ((n),(k) )(−1)^k x^k =1+Σ_(k=1) ^n ((n),(k) )(−1)^k x^k (x∈R) {Binomial theorem) ⇒∫_1 ^0 (1−x)^n dx=∫_1 ^0 {1− ((n),(1) ) x+ ((n),(2) ) x^2 − ((n),(3) ) x^3 +...+ ((n),(n) ) (−1)^n x^n }dx ∫_a ^b f(x)dx=−∫_b ^a f(x)dx (((1−x)^(n+1) )/(n+1))∣_0 ^1 =−[x−(1/2) ((n),(1) ) x^2 +(1/3) ((n),(2) ) x^3 −(1/4) ((n),(3) ) x^4 +...+(1/(n+1))(−1)^n ((n),(n) ) x^(n+1) ]_0 ^1 (((1−1)/(n+1))−(1^(n+1) /(n+1)))=−(1−(1/2) ((n),(1) )+(1/3) ((n),(3) )−(1/4) ((n),(4) )+...+(((−1)^n )/(n+1)) ((n),(n) )) −(1/(n+1))=−1+(1/2) ((n),(1) ) −(1/3) ((n),(2) ) +(1/4) ((n),(3) ) +...+(((−1)^(n+1) )/(n+1)) ((n),(n) ) (1/2) ((n),(1) ) −(1/3) ((n),(2) ) +(1/4) ((n),(3) ) +...+(((−1)^(n+1) )/(n+1)) ((n),(n) )=(n/(n+1))](https://www.tinkutara.com/question/Q7014.png)
$$\left(\mathrm{1}−{x}\right)^{{n}} =\underset{{k}=\mathrm{0}} {\overset{{n}} {\sum}}\begin{pmatrix}{{n}}\\{{k}}\end{pmatrix}\left(−\mathrm{1}\right)^{{k}} {x}^{{k}} =\mathrm{1}+\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}\begin{pmatrix}{{n}}\\{{k}}\end{pmatrix}\left(−\mathrm{1}\right)^{{k}} {x}^{{k}} \:\:\:\:\left({x}\in\mathbb{R}\right)\:\:\left\{{Binomial}\:{theorem}\right) \\ $$$$\Rightarrow\int_{\mathrm{1}} ^{\mathrm{0}} \left(\mathrm{1}−{x}\right)^{{n}} {dx}=\int_{\mathrm{1}} ^{\mathrm{0}} \left\{\mathrm{1}−\begin{pmatrix}{{n}}\\{\mathrm{1}}\end{pmatrix}\:{x}+\begin{pmatrix}{{n}}\\{\mathrm{2}}\end{pmatrix}\:{x}^{\mathrm{2}} −\begin{pmatrix}{{n}}\\{\mathrm{3}}\end{pmatrix}\:{x}^{\mathrm{3}} +…+\begin{pmatrix}{{n}}\\{{n}}\end{pmatrix}\:\left(−\mathrm{1}\right)^{{n}} {x}^{{n}} \right\}{dx} \\ $$$$\int_{{a}} ^{{b}} {f}\left({x}\right){dx}=−\int_{{b}} ^{{a}} {f}\left({x}\right){dx} \\ $$$$\frac{\left(\mathrm{1}−{x}\right)^{{n}+\mathrm{1}} }{{n}+\mathrm{1}}\mid_{\mathrm{0}} ^{\mathrm{1}} =−\left[{x}−\frac{\mathrm{1}}{\mathrm{2}}\begin{pmatrix}{{n}}\\{\mathrm{1}}\end{pmatrix}\:{x}^{\mathrm{2}} +\frac{\mathrm{1}}{\mathrm{3}}\begin{pmatrix}{{n}}\\{\mathrm{2}}\end{pmatrix}\:{x}^{\mathrm{3}} −\frac{\mathrm{1}}{\mathrm{4}}\begin{pmatrix}{{n}}\\{\mathrm{3}}\end{pmatrix}\:{x}^{\mathrm{4}} +…+\frac{\mathrm{1}}{{n}+\mathrm{1}}\left(−\mathrm{1}\right)^{{n}} \begin{pmatrix}{{n}}\\{{n}}\end{pmatrix}\:{x}^{{n}+\mathrm{1}} \right]_{\mathrm{0}} ^{\mathrm{1}} \\ $$$$\left(\frac{\mathrm{1}−\mathrm{1}}{{n}+\mathrm{1}}−\frac{\mathrm{1}^{{n}+\mathrm{1}} }{{n}+\mathrm{1}}\right)=−\left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{2}}\begin{pmatrix}{{n}}\\{\mathrm{1}}\end{pmatrix}+\frac{\mathrm{1}}{\mathrm{3}}\begin{pmatrix}{{n}}\\{\mathrm{3}}\end{pmatrix}−\frac{\mathrm{1}}{\mathrm{4}}\begin{pmatrix}{{n}}\\{\mathrm{4}}\end{pmatrix}+…+\frac{\left(−\mathrm{1}\right)^{{n}} }{{n}+\mathrm{1}}\begin{pmatrix}{{n}}\\{{n}}\end{pmatrix}\right) \\ $$$$−\frac{\mathrm{1}}{{n}+\mathrm{1}}=−\mathrm{1}+\frac{\mathrm{1}}{\mathrm{2}}\begin{pmatrix}{{n}}\\{\mathrm{1}}\end{pmatrix}\:−\frac{\mathrm{1}}{\mathrm{3}}\begin{pmatrix}{{n}}\\{\mathrm{2}}\end{pmatrix}\:+\frac{\mathrm{1}}{\mathrm{4}}\begin{pmatrix}{{n}}\\{\mathrm{3}}\end{pmatrix}\:+…+\frac{\left(−\mathrm{1}\right)^{{n}+\mathrm{1}} }{{n}+\mathrm{1}}\begin{pmatrix}{{n}}\\{{n}}\end{pmatrix} \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}\begin{pmatrix}{{n}}\\{\mathrm{1}}\end{pmatrix}\:−\frac{\mathrm{1}}{\mathrm{3}}\begin{pmatrix}{{n}}\\{\mathrm{2}}\end{pmatrix}\:+\frac{\mathrm{1}}{\mathrm{4}}\begin{pmatrix}{{n}}\\{\mathrm{3}}\end{pmatrix}\:+…+\frac{\left(−\mathrm{1}\right)^{{n}+\mathrm{1}} }{{n}+\mathrm{1}}\begin{pmatrix}{{n}}\\{{n}}\end{pmatrix}=\frac{{n}}{{n}+\mathrm{1}} \\ $$
Answered by Yozzii last updated on 08/Aug/16
$${Check}\:{for}\:{an}\:{answer}\:{in}\:{the}\:{comments}. \\ $$
