Question Number 138114 by mnjuly1970 last updated on 10/Apr/21
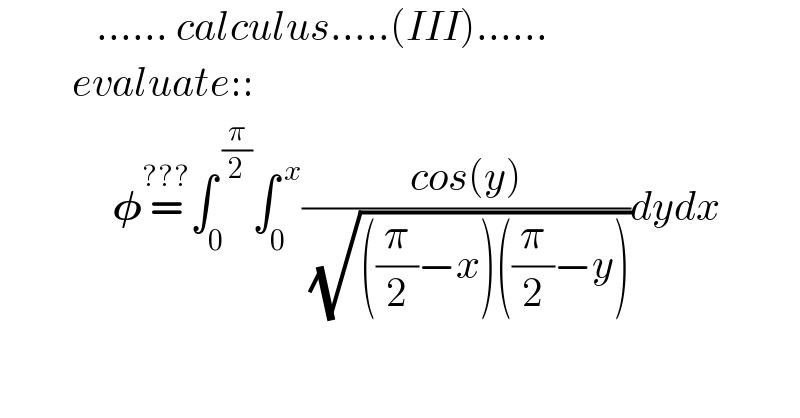
$$\:\:\:\:\:\:\:\:\:\:\:\:……\:{calculus}…..\left({III}\right)…… \\ $$$$\:\:\:\:\:\:\:\:\:{evaluate}::\:\: \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\boldsymbol{\phi}\overset{???} {=}\int_{\mathrm{0}} ^{\:\frac{\pi}{\mathrm{2}}} \int_{\mathrm{0}} ^{\:{x}} \frac{{cos}\left({y}\right)}{\:\sqrt{\left(\frac{\pi}{\mathrm{2}}−{x}\right)\left(\frac{\pi}{\mathrm{2}}−{y}\right)}}{dydx} \\ $$$$ \\ $$
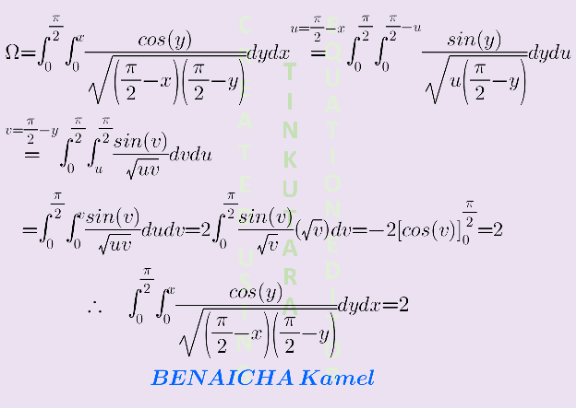
Commented by Kamel last updated on 10/Apr/21
Commented by mnjuly1970 last updated on 10/Apr/21
$${thanks}\:{alot}\:{mr}..{kamel} \\ $$
Answered by mnjuly1970 last updated on 10/Apr/21
![𝛗=∫_0 ^( (π/2)) ∫_y ^( (π/2)) ((cos(y))/( (√(((π/2)−x)((π/2)−y)))))dxdy =2∫_0 ^( (π/2)) ((cos(y))/( (√((π/2)−y)))) [−(√((π/2)−x)) ]_y ^(π/2) dy =2∫_0 ^(π/2) cos(y)dy=2sin((π/2))=2...✓](https://www.tinkutara.com/question/Q138144.png)
$$\:\:\boldsymbol{\phi}=\int_{\mathrm{0}} ^{\:\frac{\pi}{\mathrm{2}}} \int_{{y}} ^{\:\frac{\pi}{\mathrm{2}}} \frac{{cos}\left({y}\right)}{\:\sqrt{\left(\frac{\pi}{\mathrm{2}}−{x}\right)\left(\frac{\pi}{\mathrm{2}}−{y}\right)}}{dxdy} \\ $$$$=\mathrm{2}\int_{\mathrm{0}} ^{\:\frac{\pi}{\mathrm{2}}} \frac{{cos}\left({y}\right)}{\:\sqrt{\frac{\pi}{\mathrm{2}}−{y}}}\:\left[−\sqrt{\frac{\pi}{\mathrm{2}}−{x}}\:\right]_{{y}} ^{\frac{\pi}{\mathrm{2}}} {dy} \\ $$$$=\mathrm{2}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} {cos}\left({y}\right){dy}=\mathrm{2}{sin}\left(\frac{\pi}{\mathrm{2}}\right)=\mathrm{2}…\checkmark \\ $$
