Question Number 7063 by Tawakalitu. last updated on 08/Aug/16

Commented by Tawakalitu. last updated on 08/Aug/16
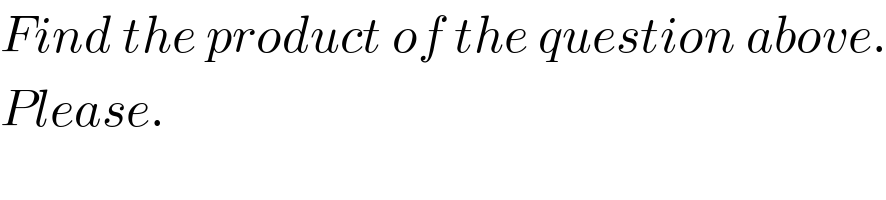
$${Find}\:{the}\:{product}\:{of}\:{the}\:{question}\:{above}. \\ $$$${Please}. \\ $$
Commented by Yozzii last updated on 08/Aug/16
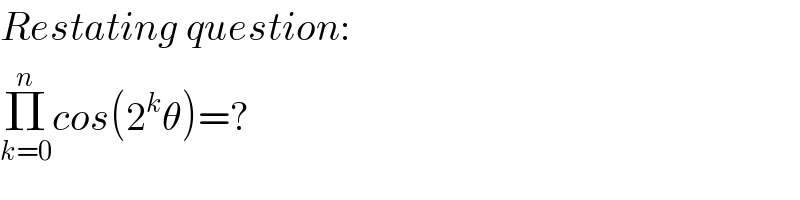
$${Restating}\:{question}: \\ $$$$\underset{{k}=\mathrm{0}} {\overset{{n}} {\prod}}{cos}\left(\mathrm{2}^{{k}} \theta\right)=? \\ $$
Commented by Yozzii last updated on 08/Aug/16
![u=cosθ cos2θ cos4θ cos8θ ×...× cos2^(n−1) θ cos2^n θ Let u(n)=Π_(k=0) ^n cos(2^k θ) Observing the result of u(n) for n=0,1,2,3 u(0)=cosθ=(1/2^0 )cosθ u(1)=cosθcos2θ=(1/2)(cos3θ+cosθ) u(2)=cosθcos2θcos4θ=0.5(0.5[cos7θ+cosθ+cos5θ+cos3θ])=(1/2^2 )[cosθ+cos3θ+cos5θ+cos7θ] u(3)=cosθcos2θcos4θcos8θ=(1/2^2 )[cos7θcos8θ+cos5θcos8θ+cos3θcos8θ+cosθcos8θ] u(3)=(1/2^3 )(cos15θ+cosθ+cos13θ+cos3θ+cos11θ+cos5θ+cos9θ+cos7θ) u(3)=(1/2^3 )(cosθ+cos3θ+cos5θ+cos7θ+cos9θ+cos11θ+cos13θ+cos15θ) I conject that u(n)=(1/2^n )Σ_(i=1) ^2^n cos[(2i−1)θ] u(n)sinθ=(1/2^n )Σ_(i=1) ^2^n sinθcos(2i−1)θ cos(2i−1)θsinθ=0.5{sin(2i)θ−sin(2i−2)θ} Let f(i)=sin2iθ 1≤i≤2^n i∈N ∴ u(n)sinθ=(1/2^(n+1) )Σ_(i=1) ^2^n {f(i)−f(i−1)} u(n)sinθ=(1/2^(n+1) )({f(1)−f(0)}+{f(2)−f(1)}+{f(3)−f(2)}+...+{f(2^n −2)−f(2^n −3)}+{f(2^n −1)−f(2^n −2)}+{f(2^n )−f(2^n −1)}) u(n)sinθ=(1/2^(n+1) )[f(2^n )−f(0)] u(n)=((sin2×2^n θ−sin(0×θ))/(2^(n+1) sinθ)) u(n)=((sin2^(n+1) θ)/(2^(n+1) sinθ)) ⇒Π_(k=0) ^n cos(2^k θ)=((sin2^(n+1) θ)/(2^(n+1) sinθ)) (θ≠mπ) n=0,1,2,3,... By induction, this formular is correct.](https://www.tinkutara.com/question/Q7069.png)
$${u}={cos}\theta\:{cos}\mathrm{2}\theta\:{cos}\mathrm{4}\theta\:{cos}\mathrm{8}\theta\:×…×\:{cos}\mathrm{2}^{{n}−\mathrm{1}} \theta\:{cos}\mathrm{2}^{{n}} \theta \\ $$$${Let}\:{u}\left({n}\right)=\underset{{k}=\mathrm{0}} {\overset{{n}} {\prod}}{cos}\left(\mathrm{2}^{{k}} \theta\right) \\ $$$${Observing}\:{the}\:{result}\:{of}\:{u}\left({n}\right)\:{for}\:{n}=\mathrm{0},\mathrm{1},\mathrm{2},\mathrm{3} \\ $$$${u}\left(\mathrm{0}\right)={cos}\theta=\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{0}} }{cos}\theta \\ $$$${u}\left(\mathrm{1}\right)={cos}\theta{cos}\mathrm{2}\theta=\frac{\mathrm{1}}{\mathrm{2}}\left({cos}\mathrm{3}\theta+{cos}\theta\right) \\ $$$${u}\left(\mathrm{2}\right)={cos}\theta{cos}\mathrm{2}\theta{cos}\mathrm{4}\theta=\mathrm{0}.\mathrm{5}\left(\mathrm{0}.\mathrm{5}\left[{cos}\mathrm{7}\theta+{cos}\theta+{cos}\mathrm{5}\theta+{cos}\mathrm{3}\theta\right]\right)=\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{2}} }\left[{cos}\theta+{cos}\mathrm{3}\theta+{cos}\mathrm{5}\theta+{cos}\mathrm{7}\theta\right] \\ $$$${u}\left(\mathrm{3}\right)={cos}\theta{cos}\mathrm{2}\theta{cos}\mathrm{4}\theta{cos}\mathrm{8}\theta=\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{2}} }\left[{cos}\mathrm{7}\theta{cos}\mathrm{8}\theta+{cos}\mathrm{5}\theta{cos}\mathrm{8}\theta+{cos}\mathrm{3}\theta{cos}\mathrm{8}\theta+{cos}\theta{cos}\mathrm{8}\theta\right] \\ $$$${u}\left(\mathrm{3}\right)=\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{3}} }\left({cos}\mathrm{15}\theta+{cos}\theta+{cos}\mathrm{13}\theta+{cos}\mathrm{3}\theta+{cos}\mathrm{11}\theta+{cos}\mathrm{5}\theta+{cos}\mathrm{9}\theta+{cos}\mathrm{7}\theta\right) \\ $$$${u}\left(\mathrm{3}\right)=\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{3}} }\left({cos}\theta+{cos}\mathrm{3}\theta+{cos}\mathrm{5}\theta+{cos}\mathrm{7}\theta+{cos}\mathrm{9}\theta+{cos}\mathrm{11}\theta+{cos}\mathrm{13}\theta+{cos}\mathrm{15}\theta\right) \\ $$$${I}\:{conject}\:{that}\:{u}\left({n}\right)=\frac{\mathrm{1}}{\mathrm{2}^{{n}} }\underset{{i}=\mathrm{1}} {\overset{\mathrm{2}^{{n}} } {\sum}}{cos}\left[\left(\mathrm{2}{i}−\mathrm{1}\right)\theta\right] \\ $$$${u}\left({n}\right){sin}\theta=\frac{\mathrm{1}}{\mathrm{2}^{{n}} }\underset{{i}=\mathrm{1}} {\overset{\mathrm{2}^{{n}} } {\sum}}{sin}\theta{cos}\left(\mathrm{2}{i}−\mathrm{1}\right)\theta \\ $$$$ \\ $$$${cos}\left(\mathrm{2}{i}−\mathrm{1}\right)\theta{sin}\theta=\mathrm{0}.\mathrm{5}\left\{{sin}\left(\mathrm{2}{i}\right)\theta−{sin}\left(\mathrm{2}{i}−\mathrm{2}\right)\theta\right\} \\ $$$${Let}\:{f}\left({i}\right)={sin}\mathrm{2}{i}\theta\:\:\:\mathrm{1}\leqslant{i}\leqslant\mathrm{2}^{{n}} \:\:{i}\in\mathbb{N} \\ $$$$ \\ $$$$\therefore\:{u}\left({n}\right){sin}\theta=\frac{\mathrm{1}}{\mathrm{2}^{{n}+\mathrm{1}} }\underset{{i}=\mathrm{1}} {\overset{\mathrm{2}^{{n}} } {\sum}}\left\{{f}\left({i}\right)−{f}\left({i}−\mathrm{1}\right)\right\}\:\:\: \\ $$$${u}\left({n}\right){sin}\theta=\frac{\mathrm{1}}{\mathrm{2}^{{n}+\mathrm{1}} }\left(\left\{{f}\left(\mathrm{1}\right)−{f}\left(\mathrm{0}\right)\right\}+\left\{{f}\left(\mathrm{2}\right)−{f}\left(\mathrm{1}\right)\right\}+\left\{{f}\left(\mathrm{3}\right)−{f}\left(\mathrm{2}\right)\right\}+…+\left\{{f}\left(\mathrm{2}^{{n}} −\mathrm{2}\right)−{f}\left(\mathrm{2}^{{n}} −\mathrm{3}\right)\right\}+\left\{{f}\left(\mathrm{2}^{{n}} −\mathrm{1}\right)−{f}\left(\mathrm{2}^{{n}} −\mathrm{2}\right)\right\}+\left\{{f}\left(\mathrm{2}^{{n}} \right)−{f}\left(\mathrm{2}^{{n}} −\mathrm{1}\right)\right\}\right) \\ $$$${u}\left({n}\right){sin}\theta=\frac{\mathrm{1}}{\mathrm{2}^{{n}+\mathrm{1}} }\left[{f}\left(\mathrm{2}^{{n}} \right)−{f}\left(\mathrm{0}\right)\right] \\ $$$${u}\left({n}\right)=\frac{{sin}\mathrm{2}×\mathrm{2}^{{n}} \theta−{sin}\left(\mathrm{0}×\theta\right)}{\mathrm{2}^{{n}+\mathrm{1}} {sin}\theta} \\ $$$${u}\left({n}\right)=\frac{{sin}\mathrm{2}^{{n}+\mathrm{1}} \theta}{\mathrm{2}^{{n}+\mathrm{1}} {sin}\theta} \\ $$$$\Rightarrow\underset{{k}=\mathrm{0}} {\overset{{n}} {\prod}}{cos}\left(\mathrm{2}^{{k}} \theta\right)=\frac{{sin}\mathrm{2}^{{n}+\mathrm{1}} \theta}{\mathrm{2}^{{n}+\mathrm{1}} {sin}\theta}\:\:\:\:\left(\theta\neq{m}\pi\right) \\ $$$${n}=\mathrm{0},\mathrm{1},\mathrm{2},\mathrm{3},… \\ $$$${By}\:{induction},\:{this}\:{formular}\:{is}\:{correct}. \\ $$
Commented by Tawakalitu. last updated on 09/Aug/16
$${Thanks}\:{so}\:{much}.\:{i}\:{really}\:{appreciate}\:{your}\:{effort}. \\ $$
Answered by Yozzii last updated on 08/Aug/16
$${Check}\:{comments}\:{for}\:{an}\:{answer}. \\ $$
