Menu Close

Solve-for-x-1-2-x-1-2-x-14-

Tinku Tara 0 Comments
Pin




Question Number 217448 by ArshadS last updated on 14/Mar/25
Solve for x: (1+(√2) )^x +(1−(√2) )^x =14
$${Solve}\:{for}\:{x}: \\ $$$$\left(\mathrm{1}+\sqrt{\mathrm{2}}\:\right)^{{x}} +\left(\mathrm{1}−\sqrt{\mathrm{2}}\:\right)^{{x}} =\mathrm{14} \\ $$
Commented by Frix last updated on 14/Mar/25
a_n =(1+(√2))^n +(1−(√2))^n ; n∈N can be written as a_1 =2 a_2 =2 a_n =a_(n−2) +2a_(n−1) ∀n≥3 ⇒ a_3 =6 a_4 =14 a_5 =34 ...
$${a}_{{n}} =\left(\mathrm{1}+\sqrt{\mathrm{2}}\right)^{{n}} +\left(\mathrm{1}−\sqrt{\mathrm{2}}\right)^{{n}} ;\:{n}\in\mathbb{N} \\ $$$$\mathrm{can}\:\mathrm{be}\:\mathrm{written}\:\mathrm{as} \\ $$$${a}_{\mathrm{1}} =\mathrm{2} \\ $$$${a}_{\mathrm{2}} =\mathrm{2} \\ $$$${a}_{{n}} ={a}_{{n}−\mathrm{2}} +\mathrm{2}{a}_{{n}−\mathrm{1}} \forall{n}\geqslant\mathrm{3} \\ $$$$\Rightarrow \\ $$$${a}_{\mathrm{3}} =\mathrm{6} \\ $$$${a}_{\mathrm{4}} =\mathrm{14} \\ $$$${a}_{\mathrm{5}} =\mathrm{34} \\ $$$$… \\ $$
Commented by Hanuda354 last updated on 15/Mar/25
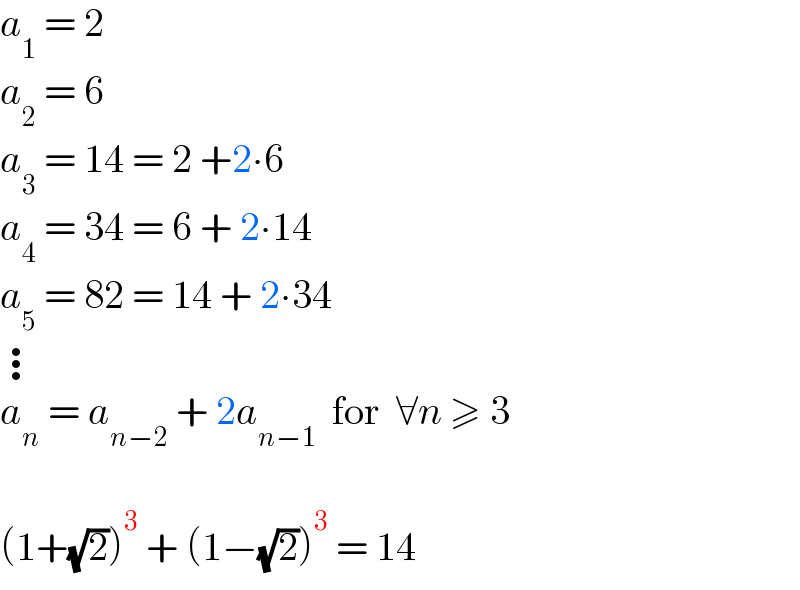
a_1 = 2 a_2 = 6 a_3 = 14 = 2 +2∙6 a_4 = 34 = 6 + 2∙14 a_5 = 82 = 14 + 2∙34 ⋮ a_n = a_(n−2) + 2a_(n−1) for ∀n ≥ 3 (1+(√2))^3 + (1−(√2))^3 = 14
$${a}_{\mathrm{1}} \:=\:\mathrm{2} \\ $$$${a}_{\mathrm{2}} \:=\:\mathrm{6} \\ $$$${a}_{\mathrm{3}} \:=\:\mathrm{14}\:=\:\mathrm{2}\:+\mathrm{2}\centerdot\mathrm{6} \\ $$$${a}_{\mathrm{4}} \:=\:\mathrm{34}\:=\:\mathrm{6}\:+\:\mathrm{2}\centerdot\mathrm{14} \\ $$$${a}_{\mathrm{5}} \:=\:\mathrm{82}\:=\:\mathrm{14}\:+\:\mathrm{2}\centerdot\mathrm{34}\: \\ $$$$\vdots \\ $$$${a}_{{n}} \:=\:{a}_{{n}−\mathrm{2}} \:+\:\mathrm{2}{a}_{{n}−\mathrm{1}} \:\:\mathrm{for}\:\:\forall{n}\:\geqslant\:\mathrm{3} \\ $$$$ \\ $$$$\left(\mathrm{1}+\sqrt{\mathrm{2}}\right)^{\mathrm{3}} \:+\:\left(\mathrm{1}−\sqrt{\mathrm{2}}\right)^{\mathrm{3}} \:=\:\mathrm{14} \\ $$
Answered by MrGaster last updated on 14/Mar/25
(1):Let a=1+(√2)∧b=1−(√2),b=−(1/a) a^x +b^x =14 for x=3: a^3 +b^3 =(1+(√2))^3 +(1−(√2))^3 (1+(√2))^3 =7+5(√2) ((1−(√2))^3 =7−5(√2) (7+5(√2))+(7+5(√2))=14 ∴x=3 f(x)=(1+(√2))^x +(1−(√2))^x ∵∣1−(√2)∣<1,The term (1−(√2) )^x decaysi exponentally.,(1+(√2))^x Exponential growth,f(x)for x>0Is strictly incrementaln ensurig a unique solution. (2):(1+(√2))^x +(1−(√2))^x =((√2))^x (((1/( (√2)))+(1/( (√2))))^x +((1/( (√2)))−(1/( (√2))))^x ) =((√2))^x (((2/( (√2))))^x +0^x )=((√2))(((√2))^x )=2^x ⇒2^x =14 ⇒x=log_2 14 x=((ln 14)/(ln 12)) x=((ln(2×7))/(ln 2))=((ln 2+ln 7)/(ln 2))=1+((ln 7)/(ln 2)) x=1+log_2 7 x=3(since log_2 7≈2.807)
$$\left(\mathrm{1}\right):\mathrm{Let}\:{a}=\mathrm{1}+\sqrt{\mathrm{2}}\wedge{b}=\mathrm{1}−\sqrt{\mathrm{2}},{b}=−\frac{\mathrm{1}}{{a}} \\ $$$${a}^{{x}} +{b}^{{x}} =\mathrm{14}\: \\ $$$$\mathrm{for}\:{x}=\mathrm{3}: \\ $$$${a}^{\mathrm{3}} +{b}^{\mathrm{3}} =\left(\mathrm{1}+\sqrt{\mathrm{2}}\right)^{\mathrm{3}} +\left(\mathrm{1}−\sqrt{\mathrm{2}}\right)^{\mathrm{3}} \\ $$$$\left(\mathrm{1}+\sqrt{\mathrm{2}}\right)^{\mathrm{3}} =\mathrm{7}+\mathrm{5}\sqrt{\mathrm{2}} \\ $$$$\left(\left(\mathrm{1}−\sqrt{\mathrm{2}}\right)^{\mathrm{3}} =\mathrm{7}−\mathrm{5}\sqrt{\mathrm{2}}\right. \\ $$$$\left(\mathrm{7}+\mathrm{5}\sqrt{\mathrm{2}}\right)+\left(\mathrm{7}+\mathrm{5}\sqrt{\mathrm{2}}\right)=\mathrm{14} \\ $$$$\therefore{x}=\mathrm{3} \\ $$$${f}\left({x}\right)=\left(\mathrm{1}+\sqrt{\mathrm{2}}\right)^{{x}} +\left(\mathrm{1}−\sqrt{\mathrm{2}}\right)^{{x}} \\ $$$$\because\mid\mathrm{1}−\sqrt{\mathrm{2}}\mid<\mathrm{1},\mathrm{The}\:\mathrm{term}\:\left(\mathrm{1}−\sqrt{\mathrm{2}}\:\right)^{{x}} \mathrm{decaysi} \\ $$$$\mathrm{exponentally}.,\left(\mathrm{1}+\sqrt{\mathrm{2}}\right)^{{x}} \mathrm{Exponential}\:\mathrm{growth},{f}\left({x}\right)\mathrm{for}\:{x}>\mathrm{0Is}\:\mathrm{strictly}\:\mathrm{incrementaln} \\ $$$$\mathrm{ensurig}\:\mathrm{a}\:\mathrm{unique}\:\mathrm{solution}. \\ $$$$\left(\mathrm{2}\right):\left(\mathrm{1}+\sqrt{\mathrm{2}}\right)^{{x}} +\left(\mathrm{1}−\sqrt{\mathrm{2}}\right)^{{x}} =\left(\sqrt{\mathrm{2}}\right)^{{x}} \left(\left(\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}+\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}\right)^{{x}} +\left(\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}−\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}\right)^{{x}} \right) \\ $$$$=\left(\sqrt{\mathrm{2}}\right)^{{x}} \left(\left(\frac{\mathrm{2}}{\:\sqrt{\mathrm{2}}}\right)^{{x}} +\mathrm{0}^{{x}} \right)=\left(\sqrt{\mathrm{2}}\right)\left(\left(\sqrt{\mathrm{2}}\right)^{{x}} \right)=\mathrm{2}^{{x}} \\ $$$$\Rightarrow\mathrm{2}^{{x}} =\mathrm{14} \\ $$$$\Rightarrow{x}=\mathrm{log}_{\mathrm{2}} \mathrm{14} \\ $$$${x}=\frac{\mathrm{ln}\:\mathrm{14}}{\mathrm{ln}\:\mathrm{12}} \\ $$$${x}=\frac{\mathrm{ln}\left(\mathrm{2}×\mathrm{7}\right)}{\mathrm{ln}\:\mathrm{2}}=\frac{\mathrm{ln}\:\mathrm{2}+\mathrm{ln}\:\mathrm{7}}{\mathrm{ln}\:\mathrm{2}}=\mathrm{1}+\frac{\mathrm{ln}\:\mathrm{7}}{\mathrm{ln}\:\mathrm{2}} \\ $$$${x}=\mathrm{1}+\mathrm{log}_{\mathrm{2}} \mathrm{7} \\ $$$${x}=\mathrm{3}\left(\mathrm{since}\:\mathrm{log}_{\mathrm{2}} \mathrm{7}\approx\mathrm{2}.\mathrm{807}\right) \\ $$
Answered by Rasheed.Sindhi last updated on 14/Mar/25
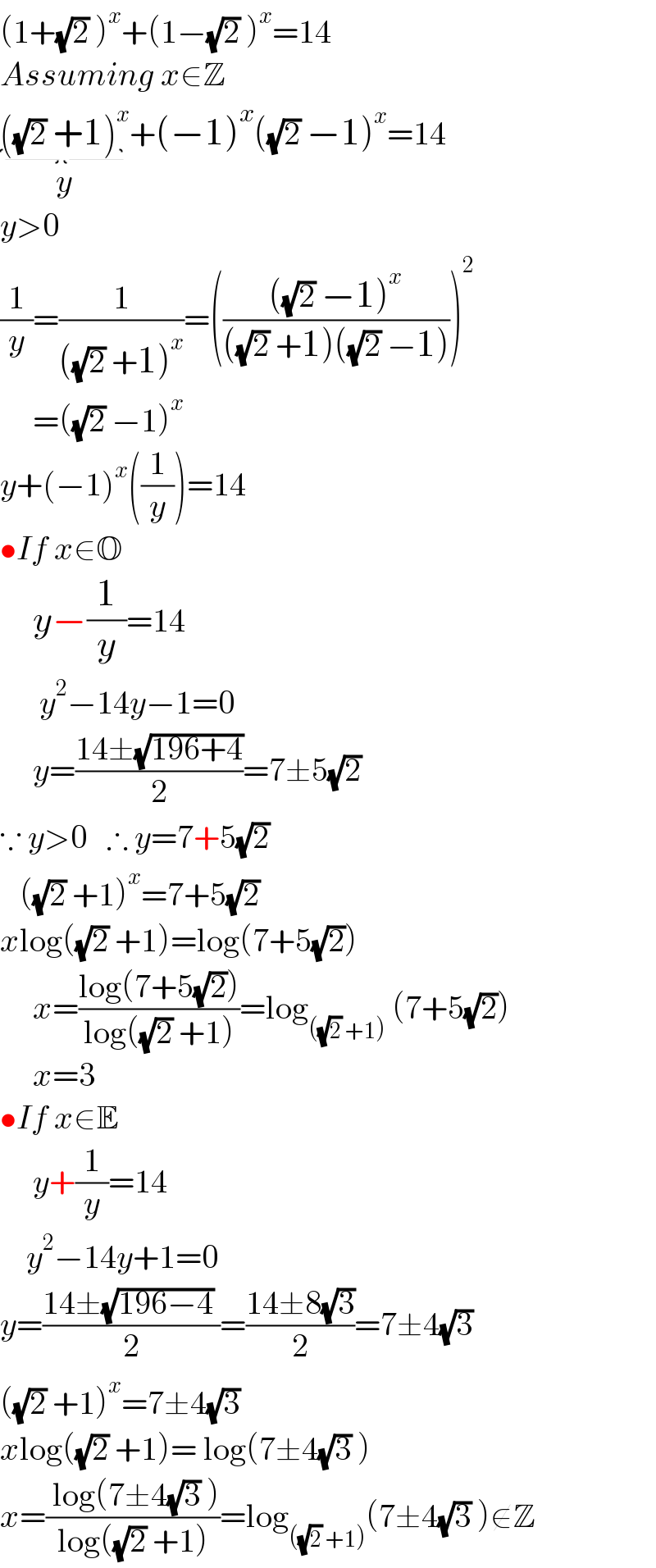
(1+(√2) )^x +(1−(√2) )^x =14 Assuming x∈Z ((√2) +1)^x _(y) +(−1)^x ((√2) −1)^x =14 y>0 (1/y)=(1/(((√2) +1)^x ))=(((((√2) −1)^x )/(((√2) +1)((√2) −1))))^2 =((√2) −1)^x y+(−1)^x ((1/y))=14 •If x∈O y−(1/y)=14 y^2 −14y−1=0 y=((14±(√(196+4)))/2)=7±5(√2) ∵ y>0 ∴ y=7+5(√2) ((√2) +1)^x =7+5(√2) xlog((√2) +1)=log(7+5(√2)) x=((log(7+5(√2)))/(log((√2) +1)))=log_(((√2) +1)) (7+5(√2)) x=3 •If x∈E y+(1/y)=14 y^2 −14y+1=0 y=((14±(√(196−4)) )/2)=((14±8(√3))/2)=7±4(√3) ((√2) +1)^x =7±4(√3) xlog((√2) +1)= log(7±4(√3) ) x=(( log(7±4(√3) ))/(log((√2) +1)))=log_(((√2) +1)) (7±4(√3) )∉Z
$$\left(\mathrm{1}+\sqrt{\mathrm{2}}\:\right)^{{x}} +\left(\mathrm{1}−\sqrt{\mathrm{2}}\:\right)^{{x}} =\mathrm{14} \\ $$$${Assuming}\:{x}\in\mathbb{Z} \\ $$$$\underset{{y}} {\underbrace{\left(\sqrt{\mathrm{2}}\:+\mathrm{1}\right)^{{x}} }}+\left(−\mathrm{1}\right)^{{x}} \left(\sqrt{\mathrm{2}}\:−\mathrm{1}\right)^{{x}} =\mathrm{14} \\ $$$${y}>\mathrm{0} \\ $$$$\frac{\mathrm{1}}{{y}}=\frac{\mathrm{1}}{\left(\sqrt{\mathrm{2}}\:+\mathrm{1}\right)^{{x}} }=\left(\frac{\left(\sqrt{\mathrm{2}}\:−\mathrm{1}\right)^{{x}} }{\left(\sqrt{\mathrm{2}}\:+\mathrm{1}\right)\left(\sqrt{\mathrm{2}}\:−\mathrm{1}\right)}\right)^{\mathrm{2}} \\ $$$$\:\:\:\:\:=\left(\sqrt{\mathrm{2}}\:−\mathrm{1}\right)^{{x}} \\ $$$${y}+\left(−\mathrm{1}\right)^{{x}} \left(\frac{\mathrm{1}}{{y}}\right)=\mathrm{14} \\ $$$$\bullet{If}\:{x}\in\mathbb{O} \\ $$$$\:\:\:\:\:{y}−\frac{\mathrm{1}}{{y}}=\mathrm{14} \\ $$$$\:\:\:\:\:\:{y}^{\mathrm{2}} −\mathrm{14}{y}−\mathrm{1}=\mathrm{0} \\ $$$$\:\:\:\:\:{y}=\frac{\mathrm{14}\pm\sqrt{\mathrm{196}+\mathrm{4}}}{\mathrm{2}}=\mathrm{7}\pm\mathrm{5}\sqrt{\mathrm{2}}\: \\ $$$$\because\:{y}>\mathrm{0}\:\:\:\therefore\:{y}=\mathrm{7}+\mathrm{5}\sqrt{\mathrm{2}}\: \\ $$$$\:\:\:\left(\sqrt{\mathrm{2}}\:+\mathrm{1}\right)^{{x}} =\mathrm{7}+\mathrm{5}\sqrt{\mathrm{2}}\: \\ $$$${x}\mathrm{log}\left(\sqrt{\mathrm{2}}\:+\mathrm{1}\right)=\mathrm{log}\left(\mathrm{7}+\mathrm{5}\sqrt{\mathrm{2}}\right)\:\: \\ $$$$\:\:\:\:\:{x}=\frac{\mathrm{log}\left(\mathrm{7}+\mathrm{5}\sqrt{\mathrm{2}}\right)}{\mathrm{log}\left(\sqrt{\mathrm{2}}\:+\mathrm{1}\right)}=\mathrm{log}_{\left(\sqrt{\mathrm{2}}\:+\mathrm{1}\right)} \:\left(\mathrm{7}+\mathrm{5}\sqrt{\mathrm{2}}\right) \\ $$$$\:\:\:\:\:{x}=\mathrm{3} \\ $$$$\bullet{If}\:{x}\in\mathbb{E} \\ $$$$\:\:\:\:\:{y}+\frac{\mathrm{1}}{{y}}=\mathrm{14} \\ $$$$\:\:\:\:{y}^{\mathrm{2}} −\mathrm{14}{y}+\mathrm{1}=\mathrm{0} \\ $$$${y}=\frac{\mathrm{14}\pm\sqrt{\mathrm{196}−\mathrm{4}}\:}{\mathrm{2}}=\frac{\mathrm{14}\pm\mathrm{8}\sqrt{\mathrm{3}}}{\mathrm{2}}=\mathrm{7}\pm\mathrm{4}\sqrt{\mathrm{3}}\: \\ $$$$\left(\sqrt{\mathrm{2}}\:+\mathrm{1}\right)^{{x}} =\mathrm{7}\pm\mathrm{4}\sqrt{\mathrm{3}}\: \\ $$$${x}\mathrm{log}\left(\sqrt{\mathrm{2}}\:+\mathrm{1}\right)=\:\mathrm{log}\left(\mathrm{7}\pm\mathrm{4}\sqrt{\mathrm{3}}\:\right) \\ $$$${x}=\frac{\:\mathrm{log}\left(\mathrm{7}\pm\mathrm{4}\sqrt{\mathrm{3}}\:\right)}{\mathrm{log}\left(\sqrt{\mathrm{2}}\:+\mathrm{1}\right)}=\mathrm{log}_{\left(\sqrt{\mathrm{2}}\:+\mathrm{1}\right)} \left(\mathrm{7}\pm\mathrm{4}\sqrt{\mathrm{3}}\:\right)\notin\mathbb{Z}\:\: \\ $$
Answered by profcedricjunior last updated on 14/Mar/25
(1+(√2))^x +(1−(√2))^x =14 =>(1+(√2))^(2x) +1−14(1+(√2))^x =0 ^(1+(√2)=t) =>t^2 −14t+1=0=>(t−7)^2 −48=0 =>(t−7−4(√3))(t−7+4(√3))=0 =>t=7−4(√3)ou t=7+4(√3) => { (((1+(√2))^x =7−4(√3))),(((1+(√2))^x =7+4(√3))) :}=> { (((1+(√2))^x =(2−(√3))^2 )),(((1+(√2))^x =(2+(√3))^2 )) :} => { ((x=((2ln(2−(√3)))/(ln(1+(√2))))=2log_((1+(√2))) (2+(√3)))),((x=((2ln(2+(√3)))/(ln(1+(√2))))=2log_((1+(√2))) (2+(√3)))) :} S_R ={2log_((1+(√2))) (2−(√3)),2log_((1+(√2))) (2+(√3))}
$$\left(\mathrm{1}+\sqrt{\mathrm{2}}\right)^{\boldsymbol{{x}}} +\left(\mathrm{1}−\sqrt{\mathrm{2}}\right)^{\boldsymbol{{x}}} =\mathrm{14} \\ $$$$=>\left(\mathrm{1}+\sqrt{\mathrm{2}}\right)^{\mathrm{2}\boldsymbol{{x}}} +\mathrm{1}−\mathrm{14}\left(\mathrm{1}+\sqrt{\mathrm{2}}\right)^{\boldsymbol{{x}}} =\mathrm{0}\overset{\mathrm{1}+\sqrt{\mathrm{2}}=\boldsymbol{{t}}} {\:} \\ $$$$=>\boldsymbol{{t}}^{\mathrm{2}} −\mathrm{14}\boldsymbol{{t}}+\mathrm{1}=\mathrm{0}=>\left(\boldsymbol{{t}}−\mathrm{7}\right)^{\mathrm{2}} −\mathrm{48}=\mathrm{0} \\ $$$$=>\left(\boldsymbol{{t}}−\mathrm{7}−\mathrm{4}\sqrt{\mathrm{3}}\right)\left(\boldsymbol{{t}}−\mathrm{7}+\mathrm{4}\sqrt{\mathrm{3}}\right)=\mathrm{0} \\ $$$$=>\boldsymbol{{t}}=\mathrm{7}−\mathrm{4}\sqrt{\mathrm{3}}\boldsymbol{{ou}}\:\boldsymbol{{t}}=\mathrm{7}+\mathrm{4}\sqrt{\mathrm{3}} \\ $$$$=>\begin{cases}{\left(\mathrm{1}+\sqrt{\mathrm{2}}\right)^{\boldsymbol{{x}}} =\mathrm{7}−\mathrm{4}\sqrt{\mathrm{3}}}\\{\left(\mathrm{1}+\sqrt{\mathrm{2}}\right)^{\boldsymbol{{x}}} =\mathrm{7}+\mathrm{4}\sqrt{\mathrm{3}}}\end{cases}=>\begin{cases}{\left(\mathrm{1}+\sqrt{\mathrm{2}}\right)^{\boldsymbol{{x}}} =\left(\mathrm{2}−\sqrt{\mathrm{3}}\right)^{\mathrm{2}} }\\{\left(\mathrm{1}+\sqrt{\mathrm{2}}\right)^{\boldsymbol{{x}}} =\left(\mathrm{2}+\sqrt{\mathrm{3}}\right)^{\mathrm{2}} }\end{cases} \\ $$$$=>\begin{cases}{\boldsymbol{{x}}=\frac{\mathrm{2}\boldsymbol{{ln}}\left(\mathrm{2}−\sqrt{\mathrm{3}}\right)}{\boldsymbol{{ln}}\left(\mathrm{1}+\sqrt{\mathrm{2}}\right)}=\mathrm{2}\boldsymbol{{log}}_{\left(\mathrm{1}+\sqrt{\mathrm{2}}\right)} \left(\mathrm{2}+\sqrt{\mathrm{3}}\right)}\\{\boldsymbol{{x}}=\frac{\mathrm{2}\boldsymbol{{ln}}\left(\mathrm{2}+\sqrt{\mathrm{3}}\right)}{\boldsymbol{{ln}}\left(\mathrm{1}+\sqrt{\mathrm{2}}\right)}=\mathrm{2}\boldsymbol{{log}}_{\left(\mathrm{1}+\sqrt{\mathrm{2}}\right)} \left(\mathrm{2}+\sqrt{\mathrm{3}}\right)}\end{cases} \\ $$$$\boldsymbol{{S}}_{\mathbb{R}} =\left\{\mathrm{2}\boldsymbol{{log}}_{\left(\mathrm{1}+\sqrt{\mathrm{2}}\right)} \left(\mathrm{2}−\sqrt{\mathrm{3}}\right),\mathrm{2}\boldsymbol{{log}}_{\left(\mathrm{1}+\sqrt{\mathrm{2}}\right)} \left(\mathrm{2}+\sqrt{\mathrm{3}}\right)\right\} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *