Question Number 139052 by EnterUsername last updated on 21/Apr/21
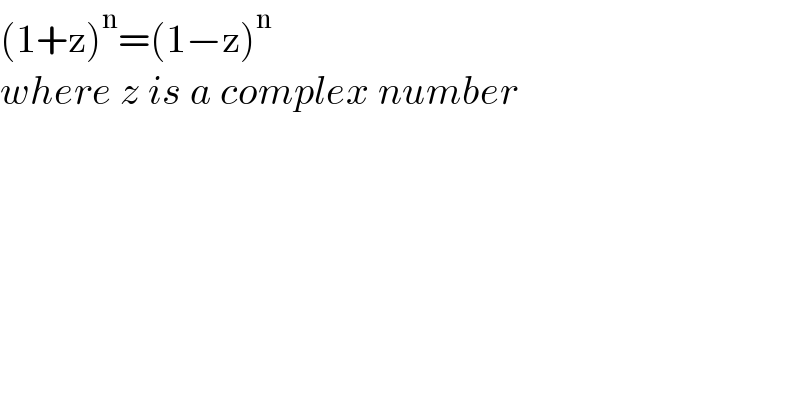
$$\left(\mathrm{1}+\mathrm{z}\right)^{\mathrm{n}} =\left(\mathrm{1}−\mathrm{z}\right)^{\mathrm{n}} \\ $$$${where}\:{z}\:{is}\:{a}\:{complex}\:{number} \\ $$
Answered by mathmax by abdo last updated on 21/Apr/21
![z=−1 is not solution let z≠−1 e⇒(((1−z)/(1+z)))^n =1 =e^(i(2kπ)) ⇒((1−z)/(1+z))=e^(i(((2kπ)/n))) k∈[[0,n−1]] ⇒1−z=e^((2ikπ)/n) +e^((2ikπ)/n) z ⇒1−e^((2ikπ)/n) =(1+e^((2ikπ)/n) )z ⇒ z_k =((1−e^((2ikπ)/n) )/(1+e^((2ikπ)/n) )) =((1−cos(((2kπ)/n))−isin(((2kπ)/n)))/(1+cos(((2kπ)/n))+isin(((2kπ)/n)))) =((2sin^2 (((kπ)/n))−2isin(((kπ)/n))cos(((kπ)/n)))/(2cos^2 (((kπ)/n))+2isin(((kπ)/n))cos(((kπ)/n)))) =((−isin(((kπ)/n))e^((ikπ)/n) )/(cos(((kπ)/n))e^((ikπ)/n) )) =−itan(((kπ)/n)) so the solution of this equation are z_k =−itan(((kπ)/n)) k∈[0,n−1]]](https://www.tinkutara.com/question/Q139064.png)
$$\mathrm{z}=−\mathrm{1}\:\mathrm{is}\:\mathrm{not}\:\mathrm{solution}\:\:\mathrm{let}\:\mathrm{z}\neq−\mathrm{1} \\ $$$$\mathrm{e}\Rightarrow\left(\frac{\mathrm{1}−\mathrm{z}}{\mathrm{1}+\mathrm{z}}\right)^{\mathrm{n}} =\mathrm{1}\:=\mathrm{e}^{\mathrm{i}\left(\mathrm{2k}\pi\right)} \:\Rightarrow\frac{\mathrm{1}−\mathrm{z}}{\mathrm{1}+\mathrm{z}}=\mathrm{e}^{\mathrm{i}\left(\frac{\mathrm{2k}\pi}{\mathrm{n}}\right)} \:\:\:\:\:\:\:\mathrm{k}\in\left[\left[\mathrm{0},\mathrm{n}−\mathrm{1}\right]\right] \\ $$$$\Rightarrow\mathrm{1}−\mathrm{z}=\mathrm{e}^{\frac{\mathrm{2ik}\pi}{\mathrm{n}}} \:+\mathrm{e}^{\frac{\mathrm{2ik}\pi}{\mathrm{n}}} \mathrm{z}\:\Rightarrow\mathrm{1}−\mathrm{e}^{\frac{\mathrm{2ik}\pi}{\mathrm{n}}} \:=\left(\mathrm{1}+\mathrm{e}^{\frac{\mathrm{2ik}\pi}{\mathrm{n}}} \right)\mathrm{z}\:\Rightarrow \\ $$$$\mathrm{z}_{\mathrm{k}} =\frac{\mathrm{1}−\mathrm{e}^{\frac{\mathrm{2ik}\pi}{\mathrm{n}}} }{\mathrm{1}+\mathrm{e}^{\frac{\mathrm{2ik}\pi}{\mathrm{n}}} }\:=\frac{\mathrm{1}−\mathrm{cos}\left(\frac{\mathrm{2k}\pi}{\mathrm{n}}\right)−\mathrm{isin}\left(\frac{\mathrm{2k}\pi}{\mathrm{n}}\right)}{\mathrm{1}+\mathrm{cos}\left(\frac{\mathrm{2k}\pi}{\mathrm{n}}\right)+\mathrm{isin}\left(\frac{\mathrm{2k}\pi}{\mathrm{n}}\right)} \\ $$$$=\frac{\mathrm{2sin}^{\mathrm{2}} \left(\frac{\mathrm{k}\pi}{\mathrm{n}}\right)−\mathrm{2isin}\left(\frac{\mathrm{k}\pi}{\mathrm{n}}\right)\mathrm{cos}\left(\frac{\mathrm{k}\pi}{\mathrm{n}}\right)}{\mathrm{2cos}^{\mathrm{2}} \left(\frac{\mathrm{k}\pi}{\mathrm{n}}\right)+\mathrm{2isin}\left(\frac{\mathrm{k}\pi}{\mathrm{n}}\right)\mathrm{cos}\left(\frac{\mathrm{k}\pi}{\mathrm{n}}\right)}\:=\frac{−\mathrm{isin}\left(\frac{\mathrm{k}\pi}{\mathrm{n}}\right)\mathrm{e}^{\frac{\mathrm{ik}\pi}{\mathrm{n}}} }{\mathrm{cos}\left(\frac{\mathrm{k}\pi}{\mathrm{n}}\right)\mathrm{e}^{\frac{\mathrm{ik}\pi}{\mathrm{n}}} }\:=−\mathrm{itan}\left(\frac{\mathrm{k}\pi}{\mathrm{n}}\right) \\ $$$$\mathrm{so}\:\mathrm{the}\:\mathrm{solution}\:\mathrm{of}\:\mathrm{this}\:\mathrm{equation}\:\mathrm{are}\:\mathrm{z}_{\mathrm{k}} =−\mathrm{itan}\left(\frac{\mathrm{k}\pi}{\mathrm{n}}\right) \\ $$$$\left.\mathrm{k}\in\left[\mathrm{0},\mathrm{n}−\mathrm{1}\right]\right] \\ $$
