Question Number 8257 by lepan last updated on 04/Oct/16
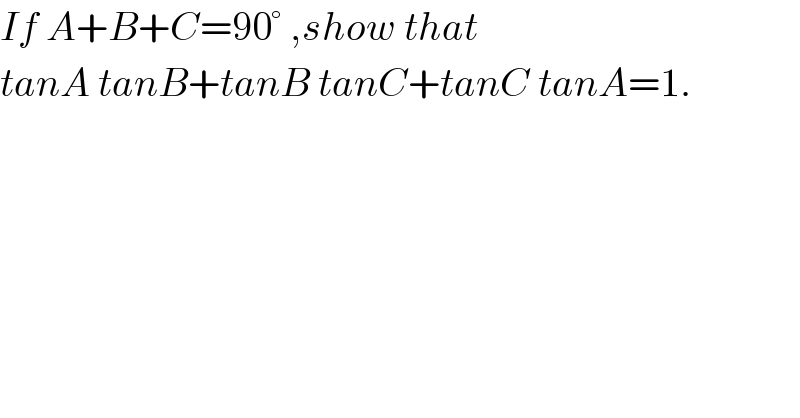
$${If}\:{A}+{B}+{C}=\mathrm{90}°\:,{show}\:{that}\: \\ $$$${tanA}\:{tanB}+{tanB}\:{tanC}+{tanC}\:{tanA}=\mathrm{1}. \\ $$
Answered by sandy_suhendra last updated on 04/Oct/16
![=tanA tanB + tanC (tanA+tanB) =tanA tanB + tanC tan(A+B)[1−tanA tanB] =tanA tanB + tanC cotC [1−tanA tanB] =tanA tanB + 1 − tanA tanB =1 using : tan(A+B)=((tanA + tanB)/(1−tanA tanB)) ⇒ tanA + tanB=tan(A+B)[1−tanA tanB] tan (A+B)=tan (90° − C)=cotC](https://www.tinkutara.com/question/Q8258.png)
$$=\mathrm{tanA}\:\mathrm{tanB}\:+\:\mathrm{tanC}\:\left(\mathrm{tanA}+\mathrm{tanB}\right) \\ $$$$=\mathrm{tanA}\:\mathrm{tanB}\:+\:\mathrm{tanC}\:\mathrm{tan}\left(\mathrm{A}+\mathrm{B}\right)\left[\mathrm{1}−\mathrm{tanA}\:\mathrm{tanB}\right] \\ $$$$=\mathrm{tanA}\:\mathrm{tanB}\:+\:\mathrm{tanC}\:\mathrm{cotC}\:\left[\mathrm{1}−\mathrm{tanA}\:\mathrm{tanB}\right] \\ $$$$=\mathrm{tanA}\:\mathrm{tanB}\:+\:\mathrm{1}\:−\:\mathrm{tanA}\:\mathrm{tanB} \\ $$$$=\mathrm{1} \\ $$$$\mathrm{using}\:: \\ $$$$\mathrm{tan}\left(\mathrm{A}+\mathrm{B}\right)=\frac{\mathrm{tanA}\:+\:\mathrm{tanB}}{\mathrm{1}−\mathrm{tanA}\:\mathrm{tanB}}\:\:\Rightarrow\:\mathrm{tanA}\:+\:\mathrm{tanB}=\mathrm{tan}\left(\mathrm{A}+\mathrm{B}\right)\left[\mathrm{1}−\mathrm{tanA}\:\mathrm{tanB}\right] \\ $$$$\mathrm{tan}\:\left(\mathrm{A}+\mathrm{B}\right)=\mathrm{tan}\:\left(\mathrm{90}°\:−\:\mathrm{C}\right)=\mathrm{cotC} \\ $$
