Question Number 12591 by @ANTARES_VY last updated on 26/Apr/17
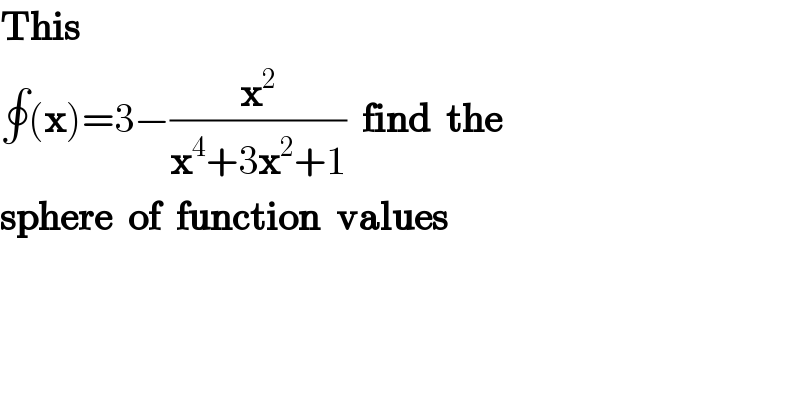
$$\boldsymbol{\mathrm{This}} \\ $$$$\oint\left(\boldsymbol{\mathrm{x}}\right)=\mathrm{3}−\frac{\boldsymbol{\mathrm{x}}^{\mathrm{2}} }{\boldsymbol{\mathrm{x}}^{\mathrm{4}} +\mathrm{3}\boldsymbol{\mathrm{x}}^{\mathrm{2}} +\mathrm{1}}\:\:\boldsymbol{\mathrm{find}}\:\:\boldsymbol{\mathrm{the}} \\ $$$$\boldsymbol{\mathrm{sphere}}\:\:\boldsymbol{\mathrm{of}}\:\:\boldsymbol{\mathrm{function}}\:\:\boldsymbol{\mathrm{values}} \\ $$
Commented by ajfour last updated on 26/Apr/17
![∮(x)=3−(1/((x+(1/x))^2 +1)) (if x≠0) at x=1 , ∮(x) has least value =3−(1/5) whenx→±∞, ∮(x) →3 and if x=0 , ∮(x)=3 so range of ∮(x) is [((14)/5),3] .](https://www.tinkutara.com/question/Q12594.png)
$$\oint\left({x}\right)=\mathrm{3}−\frac{\mathrm{1}}{\left({x}+\frac{\mathrm{1}}{{x}}\right)^{\mathrm{2}} +\mathrm{1}}\:\:\:\:\left({if}\:{x}\neq\mathrm{0}\right) \\ $$$${at}\:{x}=\mathrm{1}\:,\:\oint\left({x}\right)\:{has}\:{least}\:{value} \\ $$$$\:\:\:\:\:=\mathrm{3}−\frac{\mathrm{1}}{\mathrm{5}} \\ $$$${whenx}\rightarrow\pm\infty,\:\oint\left({x}\right)\:\rightarrow\mathrm{3} \\ $$$${and}\:{if}\:\:{x}=\mathrm{0}\:,\:\oint\left({x}\right)=\mathrm{3} \\ $$$${so}\:{range}\:{of}\:\oint\left({x}\right)\:{is}\:\left[\frac{\mathrm{14}}{\mathrm{5}},\mathrm{3}\right]\:. \\ $$
