Menu Close

x-1-and-x-2-are-solutions-of-equality-cos-pix-pi-6-sin-pix-pi-6-1-2-3-0-x-12-Find-the-value-of-x-1-x-2-

Tinku Tara 0 Comments
Pin




Question Number 143964 by naka3546 last updated on 20/Jun/21
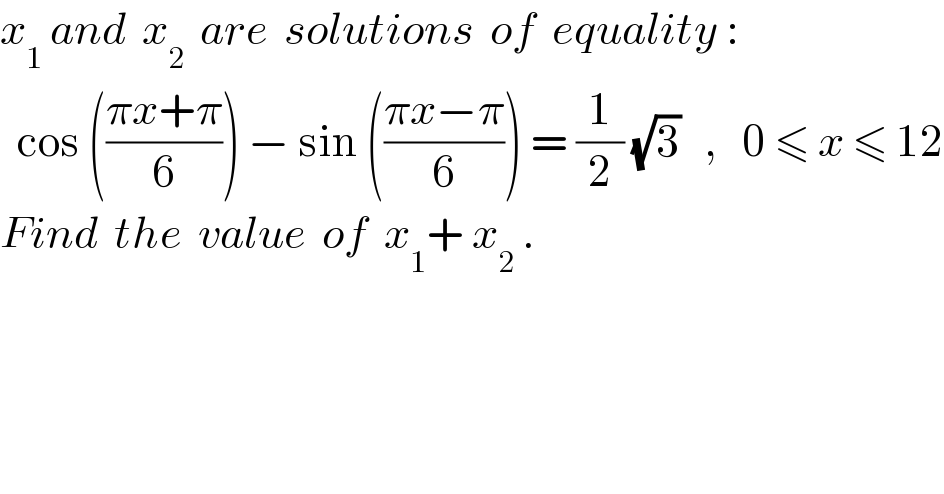
x_1 and x_2 are solutions of equality : cos (((πx+π)/6)) − sin (((πx−π)/6)) = (1/2) (√3) , 0 ≤ x ≤ 12 Find the value of x_1 + x_2 .
$${x}_{\mathrm{1}} \:{and}\:\:{x}_{\mathrm{2}} \:\:{are}\:\:{solutions}\:\:{of}\:\:{equality}\:: \\ $$$$\:\:\mathrm{cos}\:\left(\frac{\pi{x}+\pi}{\mathrm{6}}\right)\:−\:\mathrm{sin}\:\left(\frac{\pi{x}−\pi}{\mathrm{6}}\right)\:=\:\frac{\mathrm{1}}{\mathrm{2}}\:\sqrt{\mathrm{3}}\:\:\:,\:\:\:\mathrm{0}\:\leqslant\:{x}\:\leqslant\:\mathrm{12} \\ $$$${Find}\:\:{the}\:\:{value}\:\:{of}\:\:{x}_{\mathrm{1}} +\:{x}_{\mathrm{2}} \:. \\ $$
Commented by Canebulok last updated on 20/Jun/21
Solution: By squaring both sides, ⇒ cos(((πx)/6) + (π/6))−sin(((πx)/(6 )) − (π/6)) = ((√3)/2) ⇒ [cos(((πx)/6))cos((π/6))−sin(((πx)/6))sin((π/6))] − [sin(((πx)/6))cos((π/6))−cos(((πx)/6))sin((π/6))] = ((√3)/2)
$$\: \\ $$$$\boldsymbol{{Solution}}: \\ $$$${By}\:{squaring}\:{both}\:{sides}, \\ $$$$\Rightarrow\:{cos}\left(\frac{\pi{x}}{\mathrm{6}}\:+\:\frac{\pi}{\mathrm{6}}\right)−{sin}\left(\frac{\pi{x}}{\mathrm{6}\:}\:−\:\frac{\pi}{\mathrm{6}}\right)\:=\:\frac{\sqrt{\mathrm{3}}}{\mathrm{2}} \\ $$$$\Rightarrow\:\left[{cos}\left(\frac{\pi{x}}{\mathrm{6}}\right){cos}\left(\frac{\pi}{\mathrm{6}}\right)−{sin}\left(\frac{\pi{x}}{\mathrm{6}}\right){sin}\left(\frac{\pi}{\mathrm{6}}\right)\right]\:−\:\left[{sin}\left(\frac{\pi{x}}{\mathrm{6}}\right){cos}\left(\frac{\pi}{\mathrm{6}}\right)−{cos}\left(\frac{\pi{x}}{\mathrm{6}}\right){sin}\left(\frac{\pi}{\mathrm{6}}\right)\right]\:=\:\frac{\sqrt{\mathrm{3}}}{\mathrm{2}} \\ $$
Commented by Canebulok last updated on 20/Jun/21
Solution: ⇒ [cos(((πx)/6))cos((π/6))−sin(((πx)/6))cos((π/6))] + [cos(((πx)/6))sin((π/6))−sin(((πx)/6))sin((π/6))] = ((√3)/2) ⇒ cos((π/6))[cos(((πx)/6))−sin(((πx)/6))] + sin((π/6))[cos(((πx)/6))−sin(((πx)/6))] = ((√3)/2) ⇒ [cos((π/6))+sin((π/6))][cos(((πx)/6))−sin(((πx)/6))] = ((√3)/2) By squaring both sides, ⇒ [1+2cos((π/6))sin((π/6))][1−2sin(((πx)/6))cos(((πx)/6))] = (3/4) ⇒ [1+sin((π/3))][1−sin(((πx)/3))] = (3/4) ⇒ 1−sin(((πx)/3)) = (3/(4[1+sin((π/3))])) ⇒ −sin(((πx)/3)) = (3/((4+4sin((π/3))))) − 1 ⇒ sin(((πx)/3)) = 1 − (3/((4+4sin((π/3))))) ⇒ arcsin[1−(3/((4+4sin((π/3)))))] = ((πx)/3) ⇒ arcsin[1−(3/((4+4sin((π/3)))))] ((3/π)) = x ∼ Kevin
$$\boldsymbol{{Solution}}: \\ $$$$\Rightarrow\:\left[{cos}\left(\frac{\pi{x}}{\mathrm{6}}\right){cos}\left(\frac{\pi}{\mathrm{6}}\right)−{sin}\left(\frac{\pi{x}}{\mathrm{6}}\right){cos}\left(\frac{\pi}{\mathrm{6}}\right)\right]\:+\:\left[{cos}\left(\frac{\pi{x}}{\mathrm{6}}\right){sin}\left(\frac{\pi}{\mathrm{6}}\right)−{sin}\left(\frac{\pi{x}}{\mathrm{6}}\right){sin}\left(\frac{\pi}{\mathrm{6}}\right)\right]\:=\:\frac{\sqrt{\mathrm{3}}}{\mathrm{2}} \\ $$$$\Rightarrow\:{cos}\left(\frac{\pi}{\mathrm{6}}\right)\left[{cos}\left(\frac{\pi{x}}{\mathrm{6}}\right)−{sin}\left(\frac{\pi{x}}{\mathrm{6}}\right)\right]\:+\:{sin}\left(\frac{\pi}{\mathrm{6}}\right)\left[{cos}\left(\frac{\pi{x}}{\mathrm{6}}\right)−{sin}\left(\frac{\pi{x}}{\mathrm{6}}\right)\right]\:=\:\frac{\sqrt{\mathrm{3}}}{\mathrm{2}} \\ $$$$\Rightarrow\:\left[{cos}\left(\frac{\pi}{\mathrm{6}}\right)+{sin}\left(\frac{\pi}{\mathrm{6}}\right)\right]\left[{cos}\left(\frac{\pi{x}}{\mathrm{6}}\right)−{sin}\left(\frac{\pi{x}}{\mathrm{6}}\right)\right]\:=\:\frac{\sqrt{\mathrm{3}}}{\mathrm{2}} \\ $$$$\: \\ $$$${By}\:{squaring}\:{both}\:{sides}, \\ $$$$\Rightarrow\:\left[\mathrm{1}+\mathrm{2}{cos}\left(\frac{\pi}{\mathrm{6}}\right){sin}\left(\frac{\pi}{\mathrm{6}}\right)\right]\left[\mathrm{1}−\mathrm{2}{sin}\left(\frac{\pi{x}}{\mathrm{6}}\right){cos}\left(\frac{\pi{x}}{\mathrm{6}}\right)\right]\:=\:\frac{\mathrm{3}}{\mathrm{4}} \\ $$$$\Rightarrow\:\left[\mathrm{1}+{sin}\left(\frac{\pi}{\mathrm{3}}\right)\right]\left[\mathrm{1}−{sin}\left(\frac{\pi{x}}{\mathrm{3}}\right)\right]\:=\:\frac{\mathrm{3}}{\mathrm{4}} \\ $$$$\Rightarrow\:\mathrm{1}−{sin}\left(\frac{\pi{x}}{\mathrm{3}}\right)\:=\:\frac{\mathrm{3}}{\mathrm{4}\left[\mathrm{1}+{sin}\left(\frac{\pi}{\mathrm{3}}\right)\right]} \\ $$$$\: \\ $$$$\Rightarrow\:−{sin}\left(\frac{\pi{x}}{\mathrm{3}}\right)\:=\:\frac{\mathrm{3}}{\left(\mathrm{4}+\mathrm{4}{sin}\left(\frac{\pi}{\mathrm{3}}\right)\right)}\:−\:\mathrm{1} \\ $$$$\: \\ $$$$\Rightarrow\:{sin}\left(\frac{\pi{x}}{\mathrm{3}}\right)\:=\:\mathrm{1}\:−\:\frac{\mathrm{3}}{\left(\mathrm{4}+\mathrm{4}{sin}\left(\frac{\pi}{\mathrm{3}}\right)\right)} \\ $$$$\Rightarrow\:{arcsin}\left[\mathrm{1}−\frac{\mathrm{3}}{\left(\mathrm{4}+\mathrm{4}{sin}\left(\frac{\pi}{\mathrm{3}}\right)\right)}\right]\:=\:\frac{\pi{x}}{\mathrm{3}} \\ $$$$\Rightarrow\:{arcsin}\left[\mathrm{1}−\frac{\mathrm{3}}{\left(\mathrm{4}+\mathrm{4}{sin}\left(\frac{\pi}{\mathrm{3}}\right)\right)}\right]\:\left(\frac{\mathrm{3}}{\pi}\right)\:=\:{x} \\ $$$$\: \\ $$$$\sim\:{Kevin} \\ $$
Answered by bramlexs22 last updated on 20/Jun/21
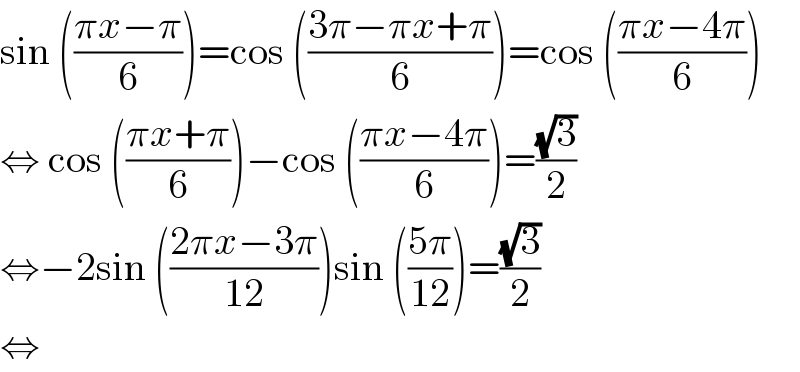
sin (((πx−π)/6))=cos (((3π−πx+π)/6))=cos (((πx−4π)/6)) ⇔ cos (((πx+π)/6))−cos (((πx−4π)/6))=((√3)/2) ⇔−2sin (((2πx−3π)/(12)))sin (((5π)/(12)))=((√3)/2) ⇔
$$\mathrm{sin}\:\left(\frac{\pi{x}−\pi}{\mathrm{6}}\right)=\mathrm{cos}\:\left(\frac{\mathrm{3}\pi−\pi{x}+\pi}{\mathrm{6}}\right)=\mathrm{cos}\:\left(\frac{\pi{x}−\mathrm{4}\pi}{\mathrm{6}}\right) \\ $$$$\Leftrightarrow\:\mathrm{cos}\:\left(\frac{\pi{x}+\pi}{\mathrm{6}}\right)−\mathrm{cos}\:\left(\frac{\pi{x}−\mathrm{4}\pi}{\mathrm{6}}\right)=\frac{\sqrt{\mathrm{3}}}{\mathrm{2}} \\ $$$$\Leftrightarrow−\mathrm{2sin}\:\left(\frac{\mathrm{2}\pi{x}−\mathrm{3}\pi}{\mathrm{12}}\right)\mathrm{sin}\:\left(\frac{\mathrm{5}\pi}{\mathrm{12}}\right)=\frac{\sqrt{\mathrm{3}}}{\mathrm{2}} \\ $$$$\Leftrightarrow\: \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *