Question Number 144074 by bobhans last updated on 21/Jun/21
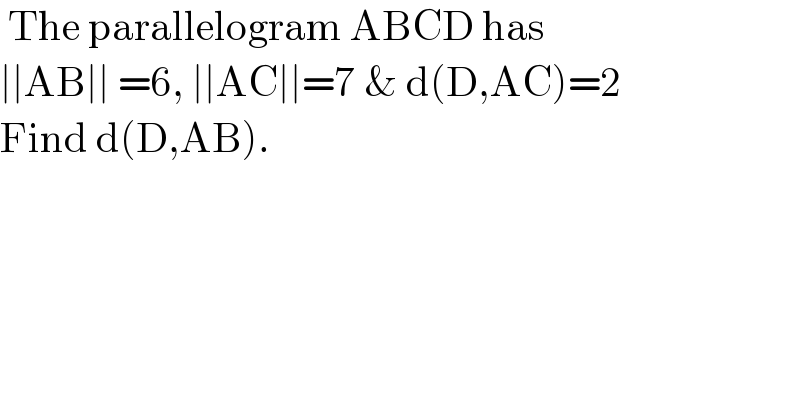
$$\:\mathrm{The}\:\mathrm{parallelogram}\:\mathrm{ABCD}\:\mathrm{has} \\ $$$$\mid\mid\mathrm{AB}\mid\mid\:=\mathrm{6},\:\mid\mid\mathrm{AC}\mid\mid=\mathrm{7}\:\&\:\mathrm{d}\left(\mathrm{D},\mathrm{AC}\right)=\mathrm{2} \\ $$$$\mathrm{Find}\:\mathrm{d}\left(\mathrm{D},\mathrm{AB}\right). \\ $$
Answered by liberty last updated on 21/Jun/21
![Area_(ΔADC) = ((2×7)/2)=7 Area_(□ABCD) = 2×[ area_(ΔADC) ]= 14 Area_(□ABCD) = AB×DF = 14 ∣∣DF∣∣ = ((14)/6) = (7/3).](https://www.tinkutara.com/question/Q144075.png)
$$\mathrm{Area}_{\Delta\mathrm{ADC}} \:=\:\frac{\mathrm{2}×\mathrm{7}}{\mathrm{2}}=\mathrm{7} \\ $$$$\mathrm{Area}_{\Box\mathrm{ABCD}} \:=\:\mathrm{2}×\left[\:\mathrm{area}_{\Delta\mathrm{ADC}} \:\right]=\:\mathrm{14} \\ $$$$\mathrm{Area}_{\Box\mathrm{ABCD}} \:=\:\mathrm{AB}×\mathrm{DF}\:=\:\mathrm{14} \\ $$$$\mid\mid\mathrm{DF}\mid\mid\:=\:\frac{\mathrm{14}}{\mathrm{6}}\:=\:\frac{\mathrm{7}}{\mathrm{3}}. \\ $$
