Question Number 144152 by SOMEDAVONG last updated on 22/Jun/21
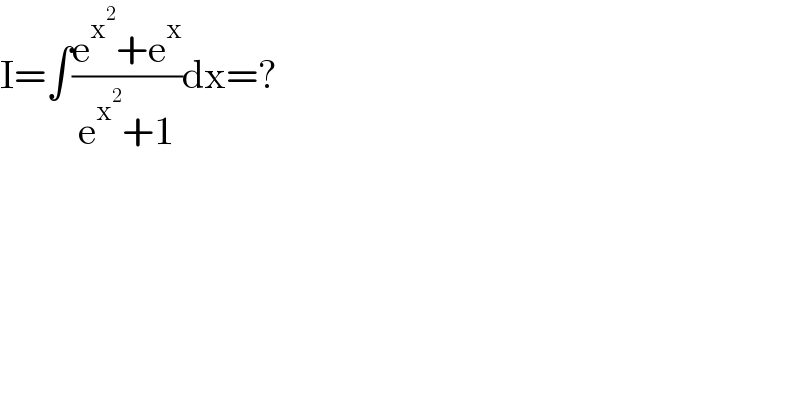
$$\mathrm{I}=\int\frac{\mathrm{e}^{\mathrm{x}^{\mathrm{2}} } +\mathrm{e}^{\mathrm{x}} }{\mathrm{e}^{\mathrm{x}^{\mathrm{2}} } +\mathrm{1}}\mathrm{dx}=? \\ $$
Answered by ArielVyny last updated on 22/Jun/21
![=∫(e^x^2 /(e^x^2 +1))dx+∫(e^x /(e^x^2 +1))dx e^x^2 =u 2xe^x^2 dx=du x^2 =ln(u) x=(1/2)ln(u) e^x =(√u) e^x dx=(1/(2(√u)))du ∫((ln(u))/(u+1))du+∫(1/(2(√u)))×(1/(u+1))du ∫((ln(u))/(u+1))du+∫((√u)/(2u))×(1/(u+1))du ∫Σ_(n≥0) (−1)^n u^n ln(u)+∫Σ_(n≥0) (−1)^n u^(n+(3/2)) Σ_(n≥0) (−1)^n ∫u^n ln(u)du+Σ_(n≥0) (−1)^n ∫u^(n+(3/2)) du ∫u^n ln(u)du=[(1/(n+1))u^(n+1) ln(u)]−(1/(n+1))∫u^n =[(1/(n+1))u^(n+1) ln(u)]−(1/((n+1)^2 ))u^(n+1) ∫u^(n+(3/2)) du=(2/(2n+5))u^(n+(5/2)) I=Σ_(n≥0) (−1)^n [((u^(n+1) ln(u))/(n+1))−(1/((n+1)^2 ))u^(n+1) ]+Σ_(n≥0) (((−1)^n )/(2n+5))u^](https://www.tinkutara.com/question/Q144153.png)
$$=\int\frac{{e}^{{x}^{\mathrm{2}} } }{{e}^{{x}^{\mathrm{2}} } +\mathrm{1}}{dx}+\int\frac{{e}^{{x}} }{{e}^{{x}^{\mathrm{2}} } +\mathrm{1}}{dx} \\ $$$${e}^{{x}^{\mathrm{2}} } ={u}\:\:\:\mathrm{2}{xe}^{{x}^{\mathrm{2}} } {dx}={du}\:\:\:{x}^{\mathrm{2}} ={ln}\left({u}\right)\:\:\:{x}=\frac{\mathrm{1}}{\mathrm{2}}{ln}\left({u}\right) \\ $$$${e}^{{x}} =\sqrt{{u}}\:\:\:\:{e}^{{x}} {dx}=\frac{\mathrm{1}}{\mathrm{2}\sqrt{{u}}}{du} \\ $$$$\int\frac{{ln}\left({u}\right)}{{u}+\mathrm{1}}{du}+\int\frac{\mathrm{1}}{\mathrm{2}\sqrt{{u}}}×\frac{\mathrm{1}}{{u}+\mathrm{1}}{du} \\ $$$$\int\frac{{ln}\left({u}\right)}{{u}+\mathrm{1}}{du}+\int\frac{\sqrt{{u}}}{\mathrm{2}{u}}×\frac{\mathrm{1}}{{u}+\mathrm{1}}{du} \\ $$$$\int\underset{{n}\geqslant\mathrm{0}} {\sum}\left(−\mathrm{1}\right)^{{n}} {u}^{{n}} {ln}\left({u}\right)+\int\underset{{n}\geqslant\mathrm{0}} {\sum}\left(−\mathrm{1}\right)^{{n}} {u}^{{n}+\frac{\mathrm{3}}{\mathrm{2}}} \\ $$$$\underset{{n}\geqslant\mathrm{0}} {\sum}\left(−\mathrm{1}\right)^{{n}} \int{u}^{{n}} {ln}\left({u}\right){du}+\underset{{n}\geqslant\mathrm{0}} {\sum}\left(−\mathrm{1}\right)^{{n}} \int{u}^{{n}+\frac{\mathrm{3}}{\mathrm{2}}} {du} \\ $$$$\int{u}^{{n}} {ln}\left({u}\right){du}=\left[\frac{\mathrm{1}}{{n}+\mathrm{1}}{u}^{{n}+\mathrm{1}} {ln}\left({u}\right)\right]−\frac{\mathrm{1}}{{n}+\mathrm{1}}\int{u}^{{n}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\left[\frac{\mathrm{1}}{{n}+\mathrm{1}}{u}^{{n}+\mathrm{1}} {ln}\left({u}\right)\right]−\frac{\mathrm{1}}{\left({n}+\mathrm{1}\right)^{\mathrm{2}} }{u}^{{n}+\mathrm{1}} \\ $$$$\int{u}^{{n}+\frac{\mathrm{3}}{\mathrm{2}}} {du}=\frac{\mathrm{2}}{\mathrm{2}{n}+\mathrm{5}}{u}^{{n}+\frac{\mathrm{5}}{\mathrm{2}}} \\ $$$${I}=\underset{{n}\geqslant\mathrm{0}} {\sum}\left(−\mathrm{1}\right)^{{n}} \left[\frac{{u}^{{n}+\mathrm{1}} {ln}\left({u}\right)}{{n}+\mathrm{1}}−\frac{\mathrm{1}}{\left({n}+\mathrm{1}\right)^{\mathrm{2}} }{u}^{{n}+\mathrm{1}} \right]+\underset{{n}\geqslant\mathrm{0}} {\sum}\frac{\left(−\mathrm{1}\right)^{{n}} }{\mathrm{2}{n}+\mathrm{5}}{u}^{} \\ $$
Answered by Canebulok last updated on 22/Jun/21
![Solution: ⇒ ∫ ((e^x^2 +e^x )/(e^x^2 +1)) dx = I We know that, ⇒ (1/(e^x^2 +1)) = Σ_(n=0) ^∞ (−1)^n .(e^x^2 )^n Thus; ⇒ ∫ ((e^x^2 +e^x )/(e^x^2 +1)) dx = ∫ (e^x^2 +e^x )Σ_(n=0) ^∞ (−1)^n .(e^x^2 )^n dx ⇒ I = ∫ Σ_(n=0) ^∞ (−1)^n .(e^(x^2 n) ).(e^x^2 +e^x ) dx ⇒ I = Σ_(n=0) ^∞ (−1)^n .[∫ e^((x^2 n+x^2 )) dx + ∫ e^(x^2 n+x) dx] ⇒ I = Σ_(n=0) ^∞ (−1)^n .[(((√π) erfi(x(√(n+1))))/(2(√(n+1)))) + (((√π) e^(−(1/(4n))) erfi(((2xn+1)/(2(√n)))))/(2(√n)))] + C](https://www.tinkutara.com/question/Q144157.png)
$$\boldsymbol{{Solution}}: \\ $$$$\Rightarrow\:\int\:\:\frac{{e}^{{x}^{\mathrm{2}} } +{e}^{{x}} }{{e}^{{x}^{\mathrm{2}} } +\mathrm{1}}\:{dx}\:=\:{I} \\ $$$${We}\:{know}\:{that}, \\ $$$$\Rightarrow\:\frac{\mathrm{1}}{{e}^{{x}^{\mathrm{2}} } +\mathrm{1}}\:=\:\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\:\left(−\mathrm{1}\right)^{{n}} .\left({e}^{{x}^{\mathrm{2}} } \right)^{{n}} \\ $$$${Thus}; \\ $$$$\Rightarrow\:\int\:\:\frac{{e}^{{x}^{\mathrm{2}} } +{e}^{{x}} }{{e}^{{x}^{\mathrm{2}} } +\mathrm{1}}\:{dx}\:=\:\int\:\left({e}^{{x}^{\mathrm{2}} } +{e}^{{x}} \right)\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\left(−\mathrm{1}\right)^{{n}} .\left({e}^{{x}^{\mathrm{2}} } \right)^{{n}} \:{dx} \\ $$$$\Rightarrow\:{I}\:=\:\int\:\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\:\left(−\mathrm{1}\right)^{{n}} .\left({e}^{{x}^{\mathrm{2}} {n}} \right).\left({e}^{{x}^{\mathrm{2}} } +{e}^{{x}} \right)\:{dx} \\ $$$$\Rightarrow\:{I}\:=\:\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\:\left(−\mathrm{1}\right)^{{n}} .\left[\int\:{e}^{\left({x}^{\mathrm{2}} {n}+{x}^{\mathrm{2}} \right)} \:{dx}\:+\:\int\:{e}^{{x}^{\mathrm{2}} {n}+{x}} \:{dx}\right] \\ $$$$\Rightarrow\:{I}\:=\:\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\:\left(−\mathrm{1}\right)^{{n}} .\left[\frac{\sqrt{\pi}\:{erfi}\left({x}\sqrt{{n}+\mathrm{1}}\right)}{\mathrm{2}\sqrt{{n}+\mathrm{1}}}\:+\:\frac{\sqrt{\pi}\:{e}^{−\frac{\mathrm{1}}{\mathrm{4}{n}}} \:{erfi}\left(\frac{\mathrm{2}{xn}+\mathrm{1}}{\mathrm{2}\sqrt{{n}}}\right)}{\mathrm{2}\sqrt{{n}}}\right]\:+\:{C} \\ $$
