Question Number 13362 by tawa tawa last updated on 19/May/17
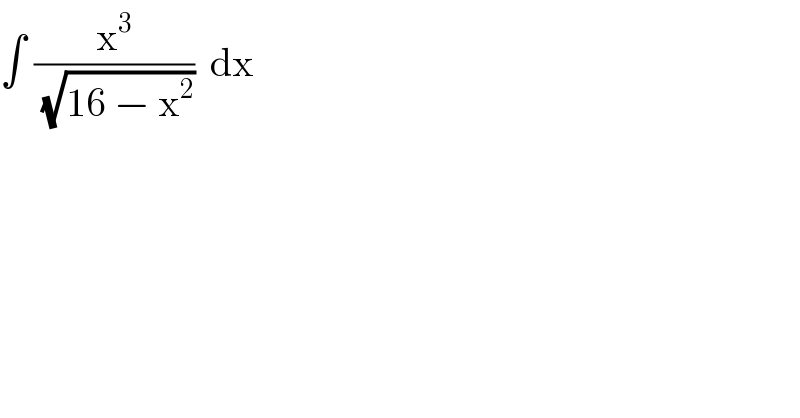
$$\int\:\frac{\mathrm{x}^{\mathrm{3}} }{\:\sqrt{\mathrm{16}\:−\:\mathrm{x}^{\mathrm{2}} }}\:\:\mathrm{dx} \\ $$
Answered by ajfour last updated on 19/May/17
![I=(1/2)∫ ((x^2 (2xdx))/( (√(16−x^2 )))) let x^2 =t ⇒ 2xdx=dt I=(1/2)∫((tdt)/( (√(16−t)))) =−(1/2)∫((16−t−16)/( (√(16−t)))) dt =−(1/2)∫(√(16−t)) dt−8∫((−dt)/( (√(16−t)))) =(1/2)[(2/3)(16−t)^(3/2) ]−8×2(√(16−t))+C as t=x^2 we have I=(1/3)(16−x^2 )^(3/2) −16(16−x^2 )^(1/2) +C .](https://www.tinkutara.com/question/Q13372.png)
$${I}=\frac{\mathrm{1}}{\mathrm{2}}\int\:\frac{{x}^{\mathrm{2}} \left(\mathrm{2}{xdx}\right)}{\:\sqrt{\mathrm{16}−{x}^{\mathrm{2}} }} \\ $$$${let}\:{x}^{\mathrm{2}} =\boldsymbol{{t}}\:\:\Rightarrow\:\:\mathrm{2}{xdx}={dt} \\ $$$${I}=\frac{\mathrm{1}}{\mathrm{2}}\int\frac{{tdt}}{\:\sqrt{\mathrm{16}−{t}}}\: \\ $$$$\:\:=−\frac{\mathrm{1}}{\mathrm{2}}\int\frac{\mathrm{16}−{t}−\mathrm{16}}{\:\sqrt{\mathrm{16}−{t}}}\:{dt} \\ $$$$\:\:=−\frac{\mathrm{1}}{\mathrm{2}}\int\sqrt{\mathrm{16}−{t}}\:{dt}−\mathrm{8}\int\frac{−{dt}}{\:\sqrt{\mathrm{16}−{t}}} \\ $$$$\:\:=\frac{\mathrm{1}}{\mathrm{2}}\left[\frac{\mathrm{2}}{\mathrm{3}}\left(\mathrm{16}−{t}\right)^{\mathrm{3}/\mathrm{2}} \right]−\mathrm{8}×\mathrm{2}\sqrt{\mathrm{16}−{t}}+{C} \\ $$$${as}\:{t}={x}^{\mathrm{2}} \:\:\:{we}\:{have} \\ $$$${I}=\frac{\mathrm{1}}{\mathrm{3}}\left(\mathrm{16}−{x}^{\mathrm{2}} \right)^{\mathrm{3}/\mathrm{2}} −\mathrm{16}\left(\mathrm{16}−{x}^{\mathrm{2}} \right)^{\mathrm{1}/\mathrm{2}} +{C}\:. \\ $$
Commented by tawa tawa last updated on 19/May/17

$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir}. \\ $$
Answered by b.e.h.i.8.3.4.1.7@gmail.com last updated on 19/May/17
![x=4sint⇒dx=4costdt cost=(√(1−(x^2 /(16))))=((√(16−x^2 ))/4) I=∫((4^3 sin^3 t.4costdt)/(4cost))=64∫sin^3 tdt =64∫sint(1−cos^2 t)dt= =64∫[sint−sintcos^2 t]dt= =64(−cost+(1/3)cos^3 t)+C= =64(−((√(16−x^2 ))/4)+(1/3).(((16−x^2 )(√(16−x^2 )))/4^3 ))+C =−(1/3)(32+x^2 )(√(16−x^2 ))+C .■](https://www.tinkutara.com/question/Q13382.png)
$${x}=\mathrm{4}{sint}\Rightarrow{dx}=\mathrm{4}{costdt} \\ $$$${cost}=\sqrt{\mathrm{1}−\frac{{x}^{\mathrm{2}} }{\mathrm{16}}}=\frac{\sqrt{\mathrm{16}−{x}^{\mathrm{2}} }}{\mathrm{4}} \\ $$$${I}=\int\frac{\mathrm{4}^{\mathrm{3}} {sin}^{\mathrm{3}} {t}.\mathrm{4}{costdt}}{\mathrm{4}{cost}}=\mathrm{64}\int{sin}^{\mathrm{3}} {tdt} \\ $$$$=\mathrm{64}\int{sint}\left(\mathrm{1}−{cos}^{\mathrm{2}} {t}\right){dt}= \\ $$$$=\mathrm{64}\int\left[{sint}−{sintcos}^{\mathrm{2}} {t}\right]{dt}= \\ $$$$=\mathrm{64}\left(−{cost}+\frac{\mathrm{1}}{\mathrm{3}}{cos}^{\mathrm{3}} {t}\right)+\boldsymbol{{C}}= \\ $$$$=\mathrm{64}\left(−\frac{\sqrt{\mathrm{16}−{x}^{\mathrm{2}} }}{\mathrm{4}}+\frac{\mathrm{1}}{\mathrm{3}}.\frac{\left(\mathrm{16}−{x}^{\mathrm{2}} \right)\sqrt{\mathrm{16}−{x}^{\mathrm{2}} }}{\mathrm{4}^{\mathrm{3}} }\right)+\boldsymbol{{C}} \\ $$$$=−\frac{\mathrm{1}}{\mathrm{3}}\left(\mathrm{32}+{x}^{\mathrm{2}} \right)\sqrt{\mathrm{16}−{x}^{\mathrm{2}} }+\boldsymbol{{C}}\:.\blacksquare \\ $$
Commented by ajfour last updated on 19/May/17

$${error}\:{in}\:{line}\:#\mathrm{5} \\ $$
Commented by b.e.h.i.8.3.4.1.7@gmail.com last updated on 19/May/17

$${thank}\:{you}\:{my}\:{friend}.{error}\:{fixed}. \\ $$
