Menu Close

0-1-ln-x-1-x-2-dx-

Tinku Tara 0 Comments
Pin




Question Number 134302 by bramlexs22 last updated on 02/Mar/21
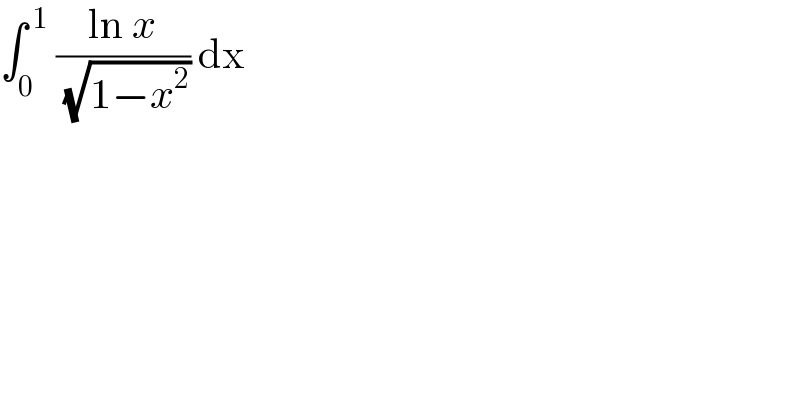
∫_0 ^( 1) ((ln x)/( (√(1−x^2 )))) dx
$$\int_{\mathrm{0}} ^{\:\mathrm{1}} \:\frac{\mathrm{ln}\:{x}}{\:\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }}\:\mathrm{dx} \\ $$
Answered by Dwaipayan Shikari last updated on 02/Mar/21
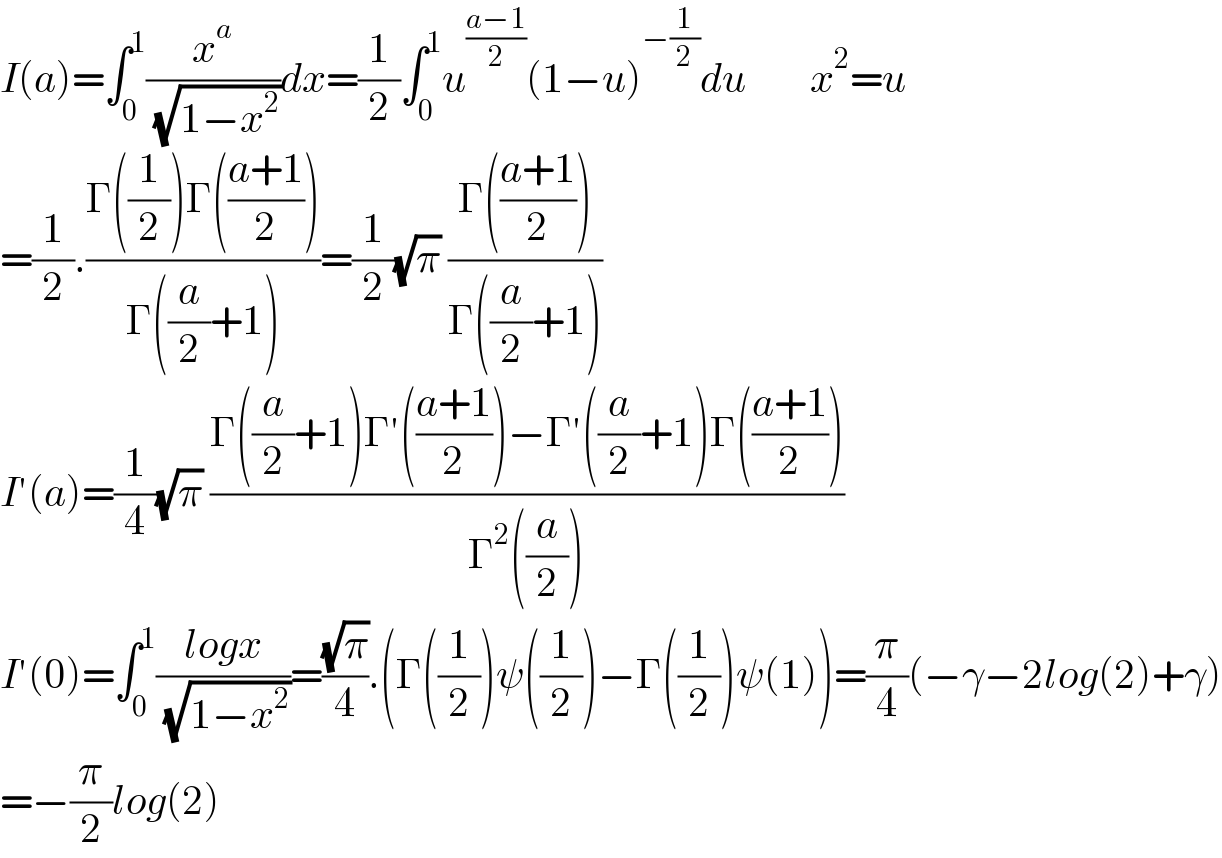
I(a)=∫_0 ^1 (x^a /( (√(1−x^2 ))))dx=(1/2)∫_0 ^1 u^((a−1)/2) (1−u)^(−(1/2)) du x^2 =u =(1/2).((Γ((1/2))Γ(((a+1)/2)))/(Γ((a/2)+1)))=(1/2)(√π) ((Γ(((a+1)/2)))/(Γ((a/2)+1))) I′(a)=(1/4)(√π) ((Γ((a/2)+1)Γ′(((a+1)/2))−Γ′((a/2)+1)Γ(((a+1)/2)))/(Γ^2 ((a/2)))) I′(0)=∫_0 ^1 ((logx)/( (√(1−x^2 ))))=((√π)/4).(Γ((1/2))ψ((1/2))−Γ((1/2))ψ(1))=(π/4)(−γ−2log(2)+γ) =−(π/2)log(2)
$${I}\left({a}\right)=\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{x}^{{a}} }{\:\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }}{dx}=\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\mathrm{1}} {u}^{\frac{{a}−\mathrm{1}}{\mathrm{2}}} \left(\mathrm{1}−{u}\right)^{−\frac{\mathrm{1}}{\mathrm{2}}} {du}\:\:\:\:\:\:\:\:{x}^{\mathrm{2}} ={u} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}.\frac{\Gamma\left(\frac{\mathrm{1}}{\mathrm{2}}\right)\Gamma\left(\frac{{a}+\mathrm{1}}{\mathrm{2}}\right)}{\Gamma\left(\frac{{a}}{\mathrm{2}}+\mathrm{1}\right)}=\frac{\mathrm{1}}{\mathrm{2}}\sqrt{\pi}\:\frac{\Gamma\left(\frac{{a}+\mathrm{1}}{\mathrm{2}}\right)}{\Gamma\left(\frac{{a}}{\mathrm{2}}+\mathrm{1}\right)} \\ $$$${I}'\left({a}\right)=\frac{\mathrm{1}}{\mathrm{4}}\sqrt{\pi}\:\frac{\Gamma\left(\frac{{a}}{\mathrm{2}}+\mathrm{1}\right)\Gamma'\left(\frac{{a}+\mathrm{1}}{\mathrm{2}}\right)−\Gamma'\left(\frac{{a}}{\mathrm{2}}+\mathrm{1}\right)\Gamma\left(\frac{{a}+\mathrm{1}}{\mathrm{2}}\right)}{\Gamma^{\mathrm{2}} \left(\frac{{a}}{\mathrm{2}}\right)} \\ $$$${I}'\left(\mathrm{0}\right)=\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{logx}}{\:\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }}=\frac{\sqrt{\pi}}{\mathrm{4}}.\left(\Gamma\left(\frac{\mathrm{1}}{\mathrm{2}}\right)\psi\left(\frac{\mathrm{1}}{\mathrm{2}}\right)−\Gamma\left(\frac{\mathrm{1}}{\mathrm{2}}\right)\psi\left(\mathrm{1}\right)\right)=\frac{\pi}{\mathrm{4}}\left(−\gamma−\mathrm{2}{log}\left(\mathrm{2}\right)+\gamma\right) \\ $$$$=−\frac{\pi}{\mathrm{2}}{log}\left(\mathrm{2}\right) \\ $$
Commented by Dwaipayan Shikari last updated on 02/Mar/21
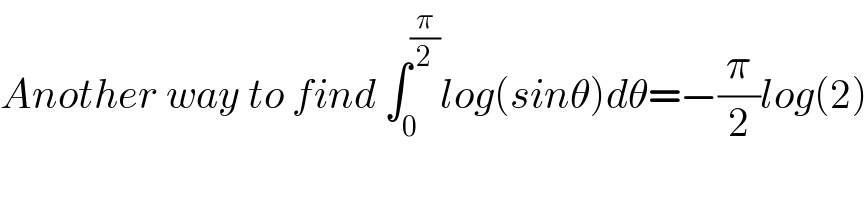
Another way to find ∫_0 ^(π/2) log(sinθ)dθ=−(π/2)log(2)
$${Another}\:{way}\:{to}\:{find}\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} {log}\left({sin}\theta\right){d}\theta=−\frac{\pi}{\mathrm{2}}{log}\left(\mathrm{2}\right) \\ $$
Commented by mnjuly1970 last updated on 02/Mar/21
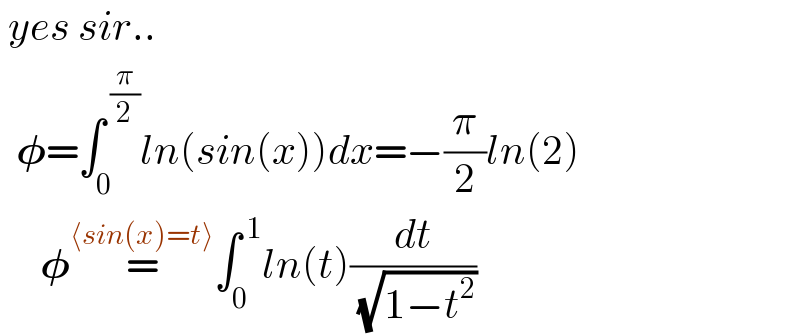
yes sir.. 𝛗=∫_0 ^( (π/2)) ln(sin(x))dx=−(π/2)ln(2) 𝛗=^(⟨sin(x)=t⟩) ∫_0 ^( 1) ln(t)(dt/( (√(1−t^2 ))))
$$\:{yes}\:{sir}.. \\ $$$$\:\:\boldsymbol{\phi}=\int_{\mathrm{0}} ^{\:\frac{\pi}{\mathrm{2}}} {ln}\left({sin}\left({x}\right)\right){dx}=−\frac{\pi}{\mathrm{2}}{ln}\left(\mathrm{2}\right) \\ $$$$\:\:\:\:\:\boldsymbol{\phi}\overset{\langle{sin}\left({x}\right)={t}\rangle} {=}\int_{\mathrm{0}} ^{\:\mathrm{1}} {ln}\left({t}\right)\frac{{dt}}{\:\sqrt{\mathrm{1}−{t}^{\mathrm{2}} }} \\ $$
Answered by bramlexs22 last updated on 02/Mar/21
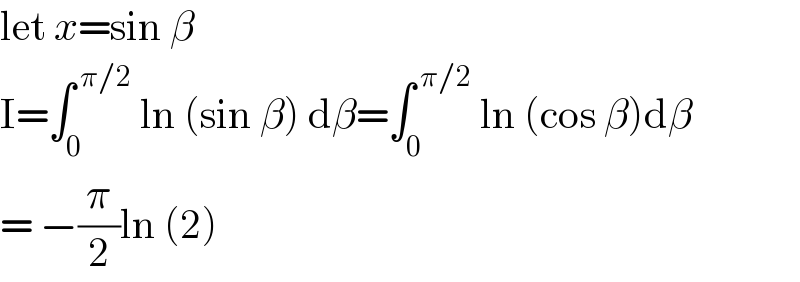
let x=sin β I=∫_0 ^( π/2) ln (sin β) dβ=∫_0 ^( π/2) ln (cos β)dβ = −(π/2)ln (2)
$$\mathrm{let}\:{x}=\mathrm{sin}\:\beta\: \\ $$$$\mathrm{I}=\int_{\mathrm{0}} ^{\:\pi/\mathrm{2}} \:\mathrm{ln}\:\left(\mathrm{sin}\:\beta\right)\:\mathrm{d}\beta=\int_{\mathrm{0}} ^{\:\pi/\mathrm{2}} \:\mathrm{ln}\:\left(\mathrm{cos}\:\beta\right)\mathrm{d}\beta \\ $$$$=\:−\frac{\pi}{\mathrm{2}}\mathrm{ln}\:\left(\mathrm{2}\right) \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *