Menu Close

0-x-f-t-dt-x-2x-tf-t-dt-0-2x-1-t-f-t-dt-f-1-2-

Tinku Tara
Pin




Question Number 329 by 123456 last updated on 23/Dec/14
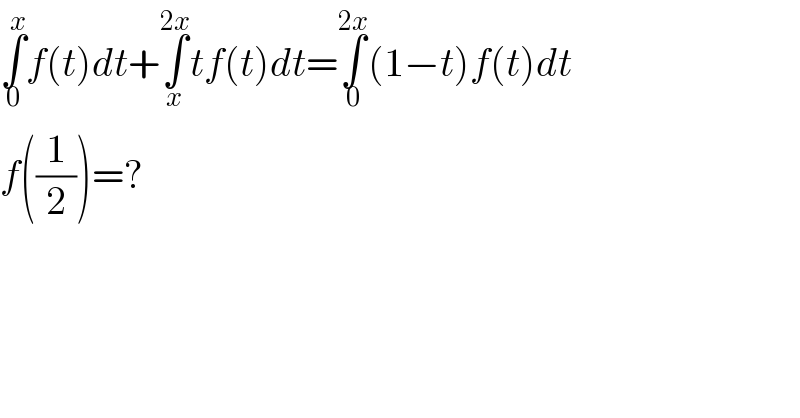
∫_0 ^x f(t)dt+∫_x ^(2x) tf(t)dt=∫_0 ^(2x) (1−t)f(t)dt f((1/2))=?
$$\underset{\mathrm{0}} {\overset{{x}} {\int}}{f}\left({t}\right){dt}+\underset{{x}} {\overset{\mathrm{2}{x}} {\int}}{tf}\left({t}\right){dt}=\underset{\mathrm{0}} {\overset{\mathrm{2}{x}} {\int}}\left(\mathrm{1}−{t}\right){f}\left({t}\right){dt} \\ $$$${f}\left(\frac{\mathrm{1}}{\mathrm{2}}\right)=? \\ $$
Commented by prakash jain last updated on 30/Dec/14
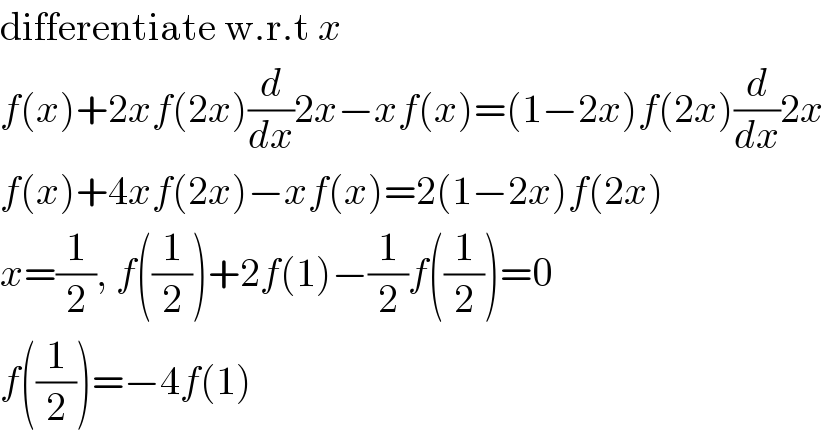
differentiate w.r.t x f(x)+2xf(2x)(d/dx)2x−xf(x)=(1−2x)f(2x)(d/dx)2x f(x)+4xf(2x)−xf(x)=2(1−2x)f(2x) x=(1/2), f((1/2))+2f(1)−(1/2)f((1/2))=0 f((1/2))=−4f(1)
$$\mathrm{differentiate}\:\mathrm{w}.\mathrm{r}.\mathrm{t}\:{x} \\ $$$${f}\left({x}\right)+\mathrm{2}{xf}\left(\mathrm{2}{x}\right)\frac{{d}}{{dx}}\mathrm{2}{x}−{xf}\left({x}\right)=\left(\mathrm{1}−\mathrm{2}{x}\right){f}\left(\mathrm{2}{x}\right)\frac{{d}}{{dx}}\mathrm{2}{x} \\ $$$${f}\left({x}\right)+\mathrm{4}{xf}\left(\mathrm{2}{x}\right)−{xf}\left({x}\right)=\mathrm{2}\left(\mathrm{1}−\mathrm{2}{x}\right){f}\left(\mathrm{2}{x}\right) \\ $$$${x}=\frac{\mathrm{1}}{\mathrm{2}},\:{f}\left(\frac{\mathrm{1}}{\mathrm{2}}\right)+\mathrm{2}{f}\left(\mathrm{1}\right)−\frac{\mathrm{1}}{\mathrm{2}}{f}\left(\frac{\mathrm{1}}{\mathrm{2}}\right)=\mathrm{0} \\ $$$${f}\left(\frac{\mathrm{1}}{\mathrm{2}}\right)=−\mathrm{4}{f}\left(\mathrm{1}\right) \\ $$

Pin