Question Number 487 by 13/NaSaNa(N)056565 last updated on 25/Jan/15

$$\int\frac{\mathrm{1}}{\mathrm{1}+\sqrt{\mathrm{2}{x}}}\:\:{dx} \\ $$
Answered by prakash jain last updated on 14/Jan/15
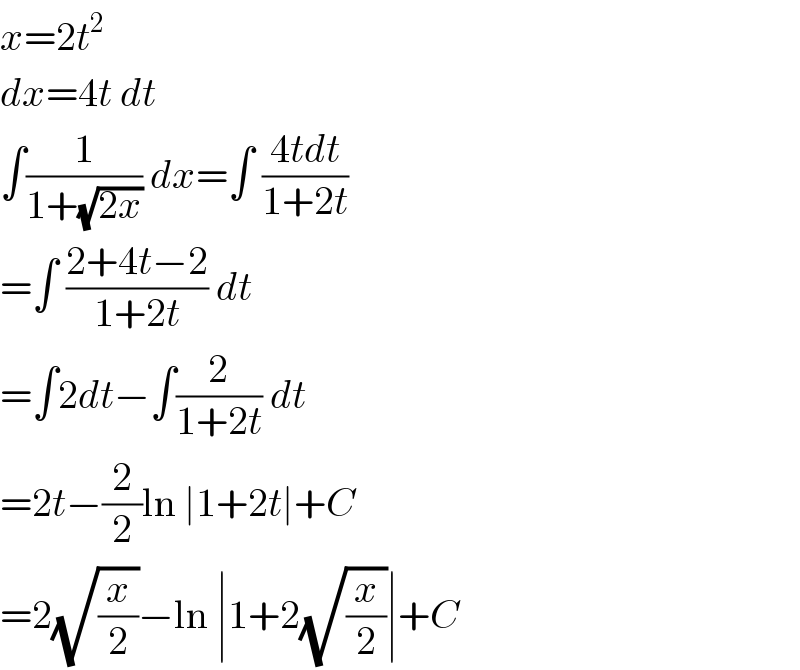
$${x}=\mathrm{2}{t}^{\mathrm{2}} \\ $$$${dx}=\mathrm{4}{t}\:{dt} \\ $$$$\int\frac{\mathrm{1}}{\mathrm{1}+\sqrt{\mathrm{2}{x}}}\:{dx}=\int\:\frac{\mathrm{4}{tdt}}{\mathrm{1}+\mathrm{2}{t}} \\ $$$$=\int\:\frac{\mathrm{2}+\mathrm{4}{t}−\mathrm{2}}{\mathrm{1}+\mathrm{2}{t}}\:{dt} \\ $$$$=\int\mathrm{2}{dt}−\int\frac{\mathrm{2}}{\mathrm{1}+\mathrm{2}{t}}\:{dt} \\ $$$$=\mathrm{2}{t}−\frac{\mathrm{2}}{\mathrm{2}}\mathrm{ln}\:\mid\mathrm{1}+\mathrm{2}{t}\mid+{C} \\ $$$$=\mathrm{2}\sqrt{\frac{{x}}{\mathrm{2}}}−\mathrm{ln}\:\mid\mathrm{1}+\mathrm{2}\sqrt{\frac{{x}}{\mathrm{2}}}\mid+{C} \\ $$
