Question Number 737 by 123456 last updated on 08/Mar/15
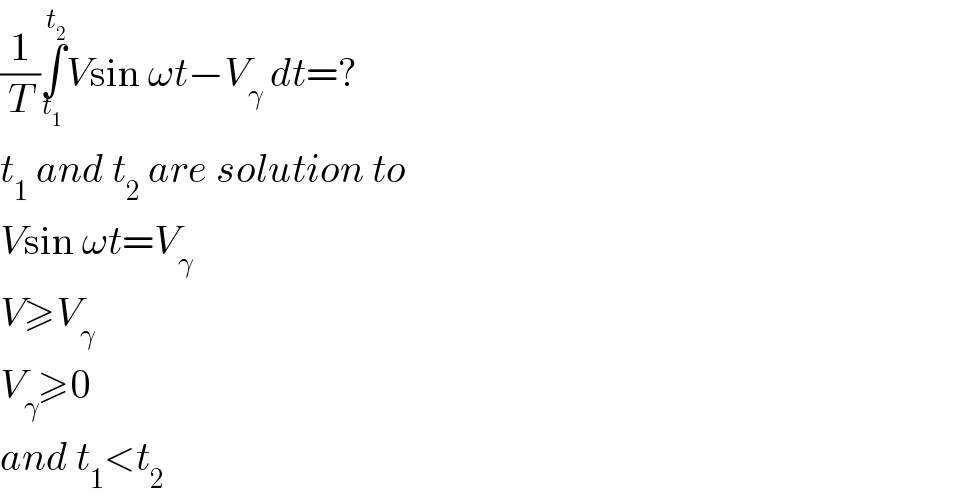
$$\frac{\mathrm{1}}{{T}}\underset{{t}_{\mathrm{1}} } {\overset{{t}_{\mathrm{2}} } {\int}}{V}\mathrm{sin}\:\omega{t}−{V}_{\gamma} \:{dt}=? \\ $$$${t}_{\mathrm{1}} \:{and}\:{t}_{\mathrm{2}} \:{are}\:{solution}\:{to} \\ $$$${V}\mathrm{sin}\:\omega{t}={V}_{\gamma} \\ $$$${V}\geqslant{V}_{\gamma} \\ $$$${V}_{\gamma} \geqslant\mathrm{0} \\ $$$${and}\:{t}_{\mathrm{1}} <{t}_{\mathrm{2}} \\ $$
Commented by prakash jain last updated on 08/Mar/15
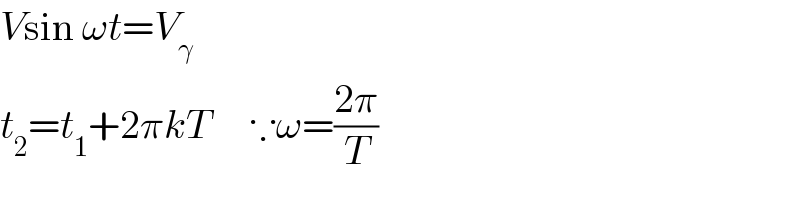
$${V}\mathrm{sin}\:\omega{t}={V}_{\gamma} \\ $$$${t}_{\mathrm{2}} ={t}_{\mathrm{1}} +\mathrm{2}\pi{kT}\:\:\:\:\:\because\omega=\frac{\mathrm{2}\pi}{{T}} \\ $$
Answered by prakash jain last updated on 08/Mar/15
![(1/T)∫Vsin ωt−V_γ dt =(1/T)[−cos ωt−V_γ t]_t_1 ^t_2 =(V_γ /T)[t_1 −t_2 ]=(V_γ /T)(−((2πk)/T)) Since sin wt_1 =sin wt_2 ⇒cos ωt_1 =cos wt_2 The given integral=− ((2πk)/T^( 2) )V_γ , k>0 V is assumed to be constant amplitude.](https://www.tinkutara.com/question/Q762.png)
$$\frac{\mathrm{1}}{{T}}\int{V}\mathrm{sin}\:\omega{t}−{V}_{\gamma} {dt} \\ $$$$=\frac{\mathrm{1}}{{T}}\left[−\mathrm{cos}\:\omega{t}−{V}_{\gamma} {t}\right]_{{t}_{\mathrm{1}} } ^{{t}_{\mathrm{2}} } =\frac{{V}_{\gamma} }{{T}}\left[{t}_{\mathrm{1}} −{t}_{\mathrm{2}} \right]=\frac{{V}_{\gamma} }{{T}}\left(−\frac{\mathrm{2}\pi{k}}{{T}}\right) \\ $$$$\mathrm{Since}\:\mathrm{sin}\:{wt}_{\mathrm{1}} =\mathrm{sin}\:{wt}_{\mathrm{2}} \Rightarrow\mathrm{cos}\:\omega{t}_{\mathrm{1}} =\mathrm{cos}\:{wt}_{\mathrm{2}} \\ $$$$\mathrm{The}\:\mathrm{given}\:\mathrm{integral}=−\:\frac{\mathrm{2}\pi{k}}{{T}^{\:\mathrm{2}} }{V}_{\gamma} \:,\:{k}>\mathrm{0} \\ $$$${V}\:\mathrm{is}\:\mathrm{assumed}\:\mathrm{to}\:\mathrm{be}\:\mathrm{constant}\:\mathrm{amplitude}. \\ $$
