Question Number 2771 by prakash jain last updated on 26/Nov/15

$$\mathrm{64}\:\mathrm{points}\:\mathrm{are}\:\mathrm{in}\:\mathrm{a}\:\mathrm{plane}: \\ $$$$\left({x},{y}\right),\:{x}\in\left\{\mathrm{0},\mathrm{1},\mathrm{2},…,\mathrm{7}\right\},\:{y}\in\left\{\mathrm{0},\mathrm{1},\mathrm{2},…,\mathrm{7}\right\} \\ $$$$\mathrm{4}\:\mathrm{points}\:\mathrm{are}\:\mathrm{chosen}\:\mathrm{at}\:\mathrm{random}. \\ $$$$\mathrm{What}\:\mathrm{is}\:\mathrm{the}\:\mathrm{proabability}\:\mathrm{the}\:\mathrm{lines}\:\mathrm{connecting} \\ $$$$\mathrm{them}\:\mathrm{do}\:\mathrm{not}\:\mathrm{form}\:\mathrm{a}\:\mathrm{square}\:\mathrm{or}\:\mathrm{rectangle}? \\ $$
Answered by Rasheed Soomro last updated on 01/Dec/15
![Please Guide me if I am wrong. I don′t know much about PROBABILITY. Assuming that sides of rectangle are horizantal and vertical. Assuming that all vertices are different points. Being P_1 P_2 ^(−) horizantal, P_1 and P_(2 ) have same y−coordinate. For same reason P_3 and P_4 have same y−coordinate. Being P_1 P_4 ^(−) and P_2 P_3 ^(−) vertical, P_1 and P_4 have same x−coordinate, and P_2 and P_(3 ) have same x−coordinate. Let P_1 =(x_1 ,y_1 ),P_2 =(x_2 ,y_1 ),P_3 (x_2 ,y_2 ) and P_4 =(x_1 ,y_2 ) where x_i ∈{0,1,2,...,7},y_i ∈{0,1,2,...,7} We first consider possibility of being rectangle/square._(−) Possibility of cboosing P_1 ,P_2 ,P_3 and P_4 is Possibility of cboosing their coordinates x_1 ,y_1 ,x_2 and y_2 Choosing x_1 has (1/8) possibility and y_1 has (1/8) possibility. Hence choosing P_1 has (1/(64)) possibility. Choosing x_2 [≠x_1 ] after choosing x_1 has (1/7) possibility. Choosing x_1 ,y_1 and x_2 has (1/8)×(1/8)×(1/7) =(1/(448)) possibility. Choosing y_(2 ) after choosing y_1 has (1/7) possibility. Choosing all the coordinates x_1 ,y_1 ,x_2 and y_2 in succesion has (1/8)×(1/8)×(1/7)×(1/7)=(1/(3136)) possibility of being_(−) rectangle. Possibility of not being_(−) rectangle=1−(1/(3136))=((3135)/(3136))](https://www.tinkutara.com/question/Q2850.png)
$$\boldsymbol{\mathrm{Please}}\:\boldsymbol{\mathrm{Guide}}\:\boldsymbol{\mathrm{me}}\:\boldsymbol{\mathrm{if}}\:\:\boldsymbol{\mathrm{I}}\:\boldsymbol{\mathrm{am}}\:\boldsymbol{\mathrm{wrong}}. \\ $$$$\boldsymbol{\mathrm{I}}\:\boldsymbol{\mathrm{don}}'\boldsymbol{\mathrm{t}}\:\boldsymbol{\mathrm{know}}\:\boldsymbol{\mathrm{much}}\:\boldsymbol{\mathrm{about}}\:\mathcal{PROBABILITY}. \\ $$$$\boldsymbol{{Assuming}}\:\boldsymbol{{that}}\:\boldsymbol{{sides}}\:\boldsymbol{{of}}\:\boldsymbol{{rectangle}}\:\boldsymbol{{are}} \\ $$$$\boldsymbol{{horizantal}}\:\boldsymbol{{and}}\:\boldsymbol{{vertical}}. \\ $$$$\boldsymbol{{Assuming}}\:\boldsymbol{{that}}\:\boldsymbol{{all}}\:\boldsymbol{{vertices}}\:\boldsymbol{{are}}\:\boldsymbol{{different}}\:\boldsymbol{{points}}. \\ $$$${Being}\:\overline {{P}_{\mathrm{1}} {P}_{\mathrm{2}} }\:\:{horizantal},\:{P}_{\mathrm{1}} \:{and}\:{P}_{\mathrm{2}\:} \:{have}\:{same}\:{y}−{coordinate}. \\ $$$${For}\:{same}\:{reason}\:{P}_{\mathrm{3}} \:{and}\:{P}_{\mathrm{4}} \:{have}\:{same}\:{y}−{coordinate}. \\ $$$${Being}\:\overline {{P}_{\mathrm{1}} {P}_{\mathrm{4}} }\:\:{and}\:\overline {{P}_{\mathrm{2}} {P}_{\mathrm{3}} }\:{vertical},\:{P}_{\mathrm{1}} \:{and}\:{P}_{\mathrm{4}} \:{have}\:{same} \\ $$$${x}−{coordinate},\:{and}\:{P}_{\mathrm{2}} \:{and}\:{P}_{\mathrm{3}\:} {have}\:{same}\:{x}−{coordinate}. \\ $$$${Let} \\ $$$${P}_{\mathrm{1}} =\left({x}_{\mathrm{1}} ,{y}_{\mathrm{1}} \right),{P}_{\mathrm{2}} =\left({x}_{\mathrm{2}} ,{y}_{\mathrm{1}} \right),{P}_{\mathrm{3}} \left({x}_{\mathrm{2}} ,{y}_{\mathrm{2}} \right)\:\:\:{and}\:\:\:{P}_{\mathrm{4}} =\left({x}_{\mathrm{1}} ,{y}_{\mathrm{2}} \right) \\ $$$${where}\:{x}_{{i}} \:\in\left\{\mathrm{0},\mathrm{1},\mathrm{2},…,\mathrm{7}\right\},{y}_{{i}} \:\in\left\{\mathrm{0},\mathrm{1},\mathrm{2},…,\mathrm{7}\right\} \\ $$$$\underset{−} {{We}\:{first}\:{consider}\:{possibility}\:{of}\:{being}\:{rectangle}/{square}.} \\ $$$$\boldsymbol{{Possibility}}\:\boldsymbol{{of}}\:\boldsymbol{{cboosing}}\:\boldsymbol{{P}}_{\mathrm{1}} ,\boldsymbol{{P}}_{\mathrm{2}} ,\boldsymbol{{P}}_{\mathrm{3}} \:\boldsymbol{{and}}\:\boldsymbol{{P}}_{\mathrm{4}} \: \\ $$$$\boldsymbol{{is}}\:\boldsymbol{{Possibility}}\:\boldsymbol{{of}}\:\boldsymbol{{cboosing}}\:\boldsymbol{{their}}\:\boldsymbol{{coordinates}} \\ $$$$\boldsymbol{{x}}_{\mathrm{1}} ,\boldsymbol{{y}}_{\mathrm{1}} ,\boldsymbol{{x}}_{\mathrm{2}} \:\:\boldsymbol{{and}}\:\boldsymbol{{y}}_{\mathrm{2}} \\ $$$$\mathcal{C}{hoosing}\:{x}_{\mathrm{1}} \:{has}\:\frac{\mathrm{1}}{\mathrm{8}}\:{possibility}\:{and}\:{y}_{\mathrm{1}} \:{has}\:\frac{\mathrm{1}}{\mathrm{8}}\:{possibility}. \\ $$$${Hence}\:{choosing}\:{P}_{\mathrm{1}} \:{has}\:\frac{\mathrm{1}}{\mathrm{64}}\:{possibility}. \\ $$$${Choosing}\:{x}_{\mathrm{2}} \:\left[\neq{x}_{\mathrm{1}} \right]\:{after}\:{choosing}\:{x}_{\mathrm{1}} \:{has}\:\frac{\mathrm{1}}{\mathrm{7}}\:{possibility}. \\ $$$${Choosing}\:{x}_{\mathrm{1}} ,{y}_{\mathrm{1}} \:{and}\:{x}_{\mathrm{2}} \:{has}\:\frac{\mathrm{1}}{\mathrm{8}}×\frac{\mathrm{1}}{\mathrm{8}}×\frac{\mathrm{1}}{\mathrm{7}}\:=\frac{\mathrm{1}}{\mathrm{448}}\:{possibility}. \\ $$$${Choosing}\:{y}_{\mathrm{2}\:} {after}\:{choosing}\:{y}_{\mathrm{1}} \:{has}\:\frac{\mathrm{1}}{\mathrm{7}}\:{possibility}.\: \\ $$$${Choosing}\:{all}\:{the}\:{coordinates}\:{x}_{\mathrm{1}} ,{y}_{\mathrm{1}} ,{x}_{\mathrm{2}} \:{and}\:\:{y}_{\mathrm{2}} \:\:{in}\:{succesion} \\ $$$${has}\:\frac{\mathrm{1}}{\mathrm{8}}×\frac{\mathrm{1}}{\mathrm{8}}×\frac{\mathrm{1}}{\mathrm{7}}×\frac{\mathrm{1}}{\mathrm{7}}=\frac{\mathrm{1}}{\mathrm{3136}}\:{possibility}\:{of}\:\underset{−} {{being}}\:{rectangle}. \\ $$$${Possibility}\:{of}\:\underset{−} {{not}\:{being}}\:{rectangle}=\mathrm{1}−\frac{\mathrm{1}}{\mathrm{3136}}=\frac{\mathrm{3135}}{\mathrm{3136}} \\ $$
Commented by prakash jain last updated on 04/Dec/15

$$\mathrm{May}\:\mathrm{the}\:\mathrm{question}\:\mathrm{was}\:\mathrm{not}\:\mathrm{clear}\:\mathrm{but}\:\mathrm{the}\:\mathrm{coordiantes} \\ $$$$\mathrm{of}\:\mathrm{the}\:\mathrm{points}\:\mathrm{are}\:\left({x},{y}\right)\:\mathrm{are}\:\left(\mathrm{0},\mathrm{0}\right)..\left(\mathrm{0},\mathrm{7}\right) \\ $$$$\left(\mathrm{1},\mathrm{0}\right)\:\mathrm{to}\:\left(\mathrm{1},\mathrm{7}\right) \\ $$$$\mathrm{so}\:\mathrm{you}\:\mathrm{know}\:\mathrm{when}\:\mathrm{two}\:\mathrm{lines}\:\mathrm{are}\:\bot^{{r}} . \\ $$
Commented by Rasheed Soomro last updated on 30/Nov/15

$$\bullet\mathcal{I}\:{understood}\:{from}\:\:{your}\:{question}:\:'{the}\:{square}\:{array} \\ $$$${of}\:\mathrm{64}\:{points}\:{of}\:{order}\:\mathrm{8}×\mathrm{8}\:{from}\:\left(\mathrm{0},\mathrm{0}\right)\:{to}\:\left(\mathrm{7},\mathrm{7}\right)'.\:{Am}\:{I}\:{wrong}? \\ $$$$\bullet{Are}\:{the}\:{sides}\:{of}\:{rectangle}\:{horizantal}\:{and}\:{vertical}\:{only}? \\ $$
Commented by Rasheed Soomro last updated on 03/Dec/15
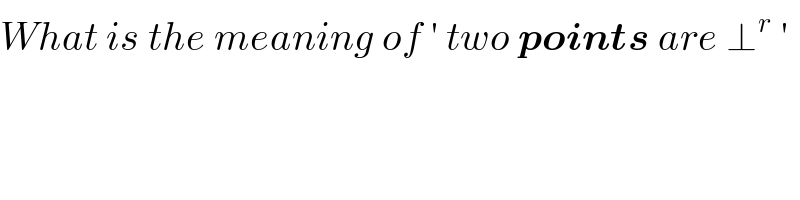
$${What}\:{is}\:{the}\:{meaning}\:{of}\:'\:{two}\:\boldsymbol{{points}}\:{are}\:\bot^{{r}} \:' \\ $$
Commented by prakash jain last updated on 04/Dec/15
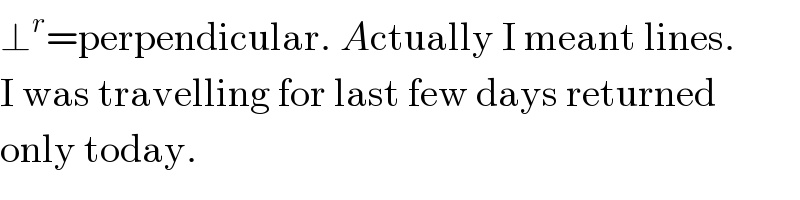
$$\bot^{{r}} =\mathrm{perpendicular}.\:{A}\mathrm{ctually}\:\mathrm{I}\:\mathrm{meant}\:\mathrm{lines}. \\ $$$$\mathrm{I}\:\mathrm{was}\:\mathrm{travelling}\:\mathrm{for}\:\mathrm{last}\:\mathrm{few}\:\mathrm{days}\:\mathrm{returned} \\ $$$$\mathrm{only}\:\mathrm{today}. \\ $$
Commented by Rasheed Soomro last updated on 04/Dec/15

$$\mathcal{T}{h}\mathcal{A}{nk}\mathcal{S}! \\ $$
