Question Number 613 by 123456 last updated on 11/Feb/15
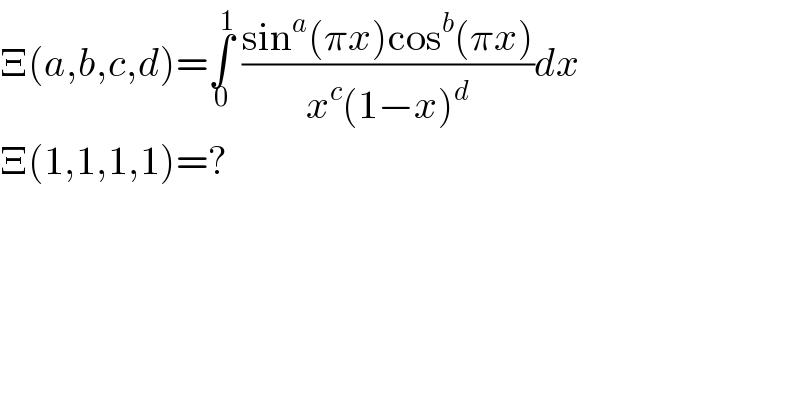
$$\Xi\left({a},{b},{c},{d}\right)=\underset{\mathrm{0}} {\overset{\mathrm{1}} {\int}}\:\frac{\mathrm{sin}^{{a}} \left(\pi{x}\right)\mathrm{cos}^{{b}} \left(\pi{x}\right)}{{x}^{{c}} \left(\mathrm{1}−{x}\right)^{{d}} }{dx} \\ $$$$\Xi\left(\mathrm{1},\mathrm{1},\mathrm{1},\mathrm{1}\right)=? \\ $$
Commented by prakash jain last updated on 10/Feb/15
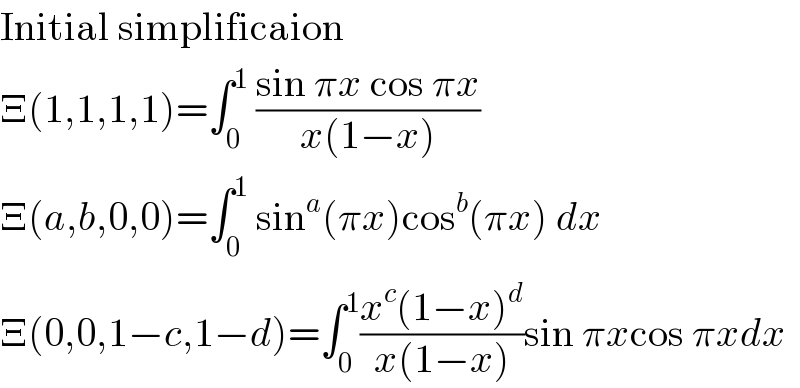
$$\mathrm{Initial}\:\mathrm{simplificaion} \\ $$$$\Xi\left(\mathrm{1},\mathrm{1},\mathrm{1},\mathrm{1}\right)=\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{\mathrm{sin}\:\pi{x}\:\mathrm{cos}\:\pi{x}}{{x}\left(\mathrm{1}−{x}\right)} \\ $$$$\Xi\left({a},{b},\mathrm{0},\mathrm{0}\right)=\int_{\mathrm{0}} ^{\mathrm{1}} \:\mathrm{sin}^{{a}} \left(\pi{x}\right)\mathrm{cos}^{{b}} \left(\pi{x}\right)\:{dx} \\ $$$$\Xi\left(\mathrm{0},\mathrm{0},\mathrm{1}−{c},\mathrm{1}−{d}\right)=\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{x}^{{c}} \left(\mathrm{1}−{x}\right)^{{d}} }{{x}\left(\mathrm{1}−{x}\right)}\mathrm{sin}\:\pi{x}\mathrm{cos}\:\pi{xdx} \\ $$
Commented by prakash jain last updated on 11/Feb/15
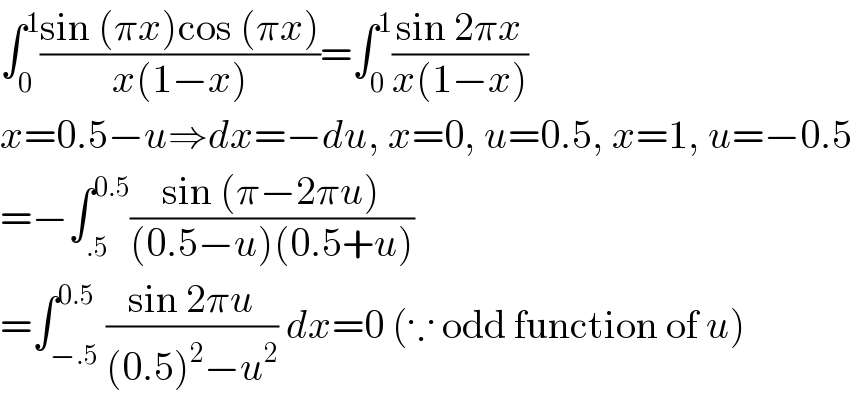
$$\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{sin}\:\left(\pi{x}\right)\mathrm{cos}\:\left(\pi{x}\right)}{{x}\left(\mathrm{1}−{x}\right)}=\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{sin}\:\mathrm{2}\pi{x}}{{x}\left(\mathrm{1}−{x}\right)} \\ $$$${x}=\mathrm{0}.\mathrm{5}−{u}\Rightarrow{dx}=−{du},\:{x}=\mathrm{0},\:{u}=\mathrm{0}.\mathrm{5},\:{x}=\mathrm{1},\:{u}=−\mathrm{0}.\mathrm{5} \\ $$$$=−\int_{.\mathrm{5}} ^{\mathrm{0}.\mathrm{5}} \frac{\mathrm{sin}\:\left(\pi−\mathrm{2}\pi{u}\right)}{\left(\mathrm{0}.\mathrm{5}−{u}\right)\left(\mathrm{0}.\mathrm{5}+{u}\right)} \\ $$$$=\int_{−.\mathrm{5}} ^{\mathrm{0}.\mathrm{5}} \frac{\mathrm{sin}\:\mathrm{2}\pi{u}}{\left(\mathrm{0}.\mathrm{5}\right)^{\mathrm{2}} −{u}^{\mathrm{2}} }\:{dx}=\mathrm{0}\:\left(\because\:\mathrm{odd}\:\mathrm{function}\:\mathrm{of}\:{u}\right) \\ $$
