Question Number 69014 by Rio Michael last updated on 17/Sep/19
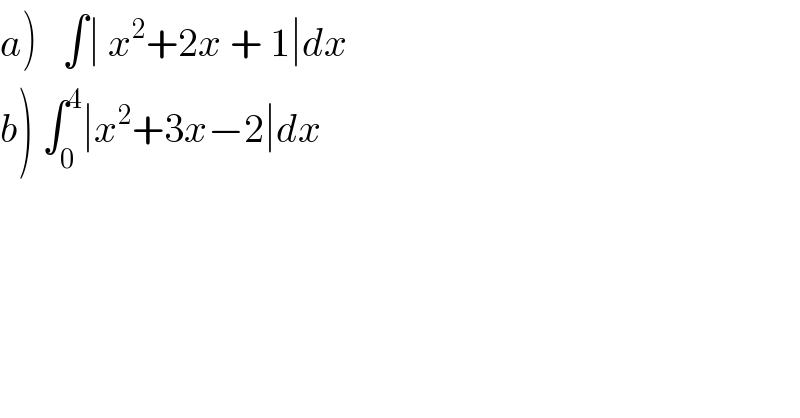
$$\left.{a}\right)\:\:\:\int\mid\:{x}^{\mathrm{2}} +\mathrm{2}{x}\:+\:\mathrm{1}\mid{dx} \\ $$$$\left.{b}\right)\:\int_{\mathrm{0}} ^{\mathrm{4}} \mid{x}^{\mathrm{2}} +\mathrm{3}{x}−\mathrm{2}\mid{dx} \\ $$
Answered by MJS last updated on 17/Sep/19
![∫∣x^2 +2x+1∣dx=∫∣(x+1)^2 ∣dx=∫(x+1)^2 dx= =(((x+1)^3 )/3)+C ∫_0 ^4 ∣x^2 +3x−2∣dx=∫_0 ^4 ∣(x+((3+(√(17)))/2))(x+((3−(√(17)))/2))∣dx= =−∫_0 ^((−3+(√(17)))/2) (x^2 +3x−2)dx+∫_((−3+(√(17)))/2) ^4 (x^2 +3x−2)dx= =−[(x^3 /3)+((3x^2 )/2)−2x]_0 ^((−3+(√(17)))/2) +[(x^3 /3)+((3x^2 )/2)−2x]_((−3+(√(17)))/2) ^4 = =((161+17(√(17)))/6)](https://www.tinkutara.com/question/Q69021.png)
$$\int\mid{x}^{\mathrm{2}} +\mathrm{2}{x}+\mathrm{1}\mid{dx}=\int\mid\left({x}+\mathrm{1}\right)^{\mathrm{2}} \mid{dx}=\int\left({x}+\mathrm{1}\right)^{\mathrm{2}} {dx}= \\ $$$$=\frac{\left({x}+\mathrm{1}\right)^{\mathrm{3}} }{\mathrm{3}}+{C} \\ $$$$ \\ $$$$\underset{\mathrm{0}} {\overset{\mathrm{4}} {\int}}\mid{x}^{\mathrm{2}} +\mathrm{3}{x}−\mathrm{2}\mid{dx}=\underset{\mathrm{0}} {\overset{\mathrm{4}} {\int}}\mid\left({x}+\frac{\mathrm{3}+\sqrt{\mathrm{17}}}{\mathrm{2}}\right)\left({x}+\frac{\mathrm{3}−\sqrt{\mathrm{17}}}{\mathrm{2}}\right)\mid{dx}= \\ $$$$=−\underset{\mathrm{0}} {\overset{\frac{−\mathrm{3}+\sqrt{\mathrm{17}}}{\mathrm{2}}} {\int}}\left({x}^{\mathrm{2}} +\mathrm{3}{x}−\mathrm{2}\right){dx}+\underset{\frac{−\mathrm{3}+\sqrt{\mathrm{17}}}{\mathrm{2}}} {\overset{\mathrm{4}} {\int}}\left({x}^{\mathrm{2}} +\mathrm{3}{x}−\mathrm{2}\right){dx}= \\ $$$$=−\left[\frac{{x}^{\mathrm{3}} }{\mathrm{3}}+\frac{\mathrm{3}{x}^{\mathrm{2}} }{\mathrm{2}}−\mathrm{2}{x}\right]_{\mathrm{0}} ^{\frac{−\mathrm{3}+\sqrt{\mathrm{17}}}{\mathrm{2}}} +\left[\frac{{x}^{\mathrm{3}} }{\mathrm{3}}+\frac{\mathrm{3}{x}^{\mathrm{2}} }{\mathrm{2}}−\mathrm{2}{x}\right]_{\frac{−\mathrm{3}+\sqrt{\mathrm{17}}}{\mathrm{2}}} ^{\mathrm{4}} = \\ $$$$=\frac{\mathrm{161}+\mathrm{17}\sqrt{\mathrm{17}}}{\mathrm{6}} \\ $$
