Question Number 133942 by mathocean1 last updated on 25/Feb/21
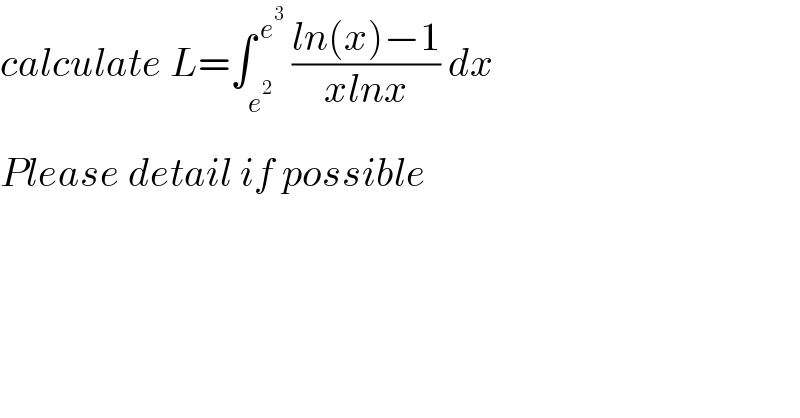
$${calculate}\:{L}=\int_{{e}^{\mathrm{2}} } ^{\:{e}^{\mathrm{3}} } \:\frac{{ln}\left({x}\right)−\mathrm{1}}{{xlnx}}\:{dx} \\ $$$${Please}\:{detail}\:{if}\:{possibl}\overset{} {{e}} \\ $$
Answered by Ñï= last updated on 25/Feb/21
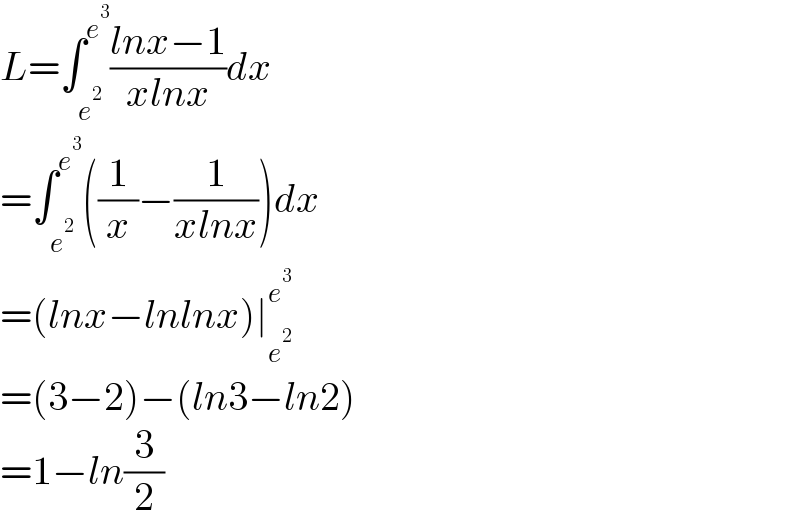
$${L}=\int_{{e}^{\mathrm{2}} } ^{{e}^{\mathrm{3}} } \frac{{lnx}−\mathrm{1}}{{xlnx}}{dx} \\ $$$$=\int_{{e}^{\mathrm{2}} } ^{{e}^{\mathrm{3}} } \left(\frac{\mathrm{1}}{{x}}−\frac{\mathrm{1}}{{xlnx}}\right){dx} \\ $$$$=\left({lnx}−{lnlnx}\right)\mid_{{e}^{\mathrm{2}} } ^{{e}^{\mathrm{3}} } \\ $$$$=\left(\mathrm{3}−\mathrm{2}\right)−\left({ln}\mathrm{3}−{ln}\mathrm{2}\right) \\ $$$$=\mathrm{1}−{ln}\frac{\mathrm{3}}{\mathrm{2}} \\ $$
Answered by mnjuly1970 last updated on 25/Feb/21
![ln(x)=u⇒(1/x)dx=du 𝛗=∫_2 ^( 3) ((u−1)/u)du [u−ln(u)]_2 ^3 =3−ln(3)−2+ln(2 =1−ln((3/2))=ln(((2e)/3))..✓](https://www.tinkutara.com/question/Q133944.png)
$${ln}\left({x}\right)={u}\Rightarrow\frac{\mathrm{1}}{{x}}{dx}={du} \\ $$$$\:\:\boldsymbol{\phi}=\int_{\mathrm{2}} ^{\:\mathrm{3}} \frac{{u}−\mathrm{1}}{{u}}{du} \\ $$$$\:\:\:\:\:\:\:\:\left[{u}−{ln}\left({u}\right)\right]_{\mathrm{2}} ^{\mathrm{3}} =\mathrm{3}−{ln}\left(\mathrm{3}\right)−\mathrm{2}+{ln}\left(\mathrm{2}\right. \\ $$$$=\mathrm{1}−{ln}\left(\frac{\mathrm{3}}{\mathrm{2}}\right)={ln}\left(\frac{\mathrm{2}{e}}{\mathrm{3}}\right)..\checkmark \\ $$
Answered by Olaf last updated on 25/Feb/21
![I = ∫_e^2 ^e^3 ((lnx−1)/(xlnx)) dx I = ∫_e^2 ^e^3 (((lnx+1)/(xlnx))−2((1/x)/(lnx))) dx I = ∫_e^2 ^e^3 (((d(xlnx))/(xlnx))−2((d(lnx))/(lnx))) I = [ln(xlnx)−2ln(lnx)]_e^2 ^e^3 I = [ln((x/(lnx)))]_e^2 ^e^3 I = ln((e^3 /3))−ln((e^2 /2)) = ln(((2e)/3)) = 1+ln(2/3)](https://www.tinkutara.com/question/Q133946.png)
$$\mathrm{I}\:=\:\int_{{e}^{\mathrm{2}} } ^{{e}^{\mathrm{3}} } \frac{\mathrm{ln}{x}−\mathrm{1}}{{x}\mathrm{ln}{x}}\:{dx} \\ $$$$\mathrm{I}\:=\:\int_{{e}^{\mathrm{2}} } ^{{e}^{\mathrm{3}} } \left(\frac{\mathrm{ln}{x}+\mathrm{1}}{{x}\mathrm{ln}{x}}−\mathrm{2}\frac{\frac{\mathrm{1}}{{x}}}{\mathrm{ln}{x}}\right)\:{dx} \\ $$$$\mathrm{I}\:=\:\int_{{e}^{\mathrm{2}} } ^{{e}^{\mathrm{3}} } \left(\frac{{d}\left({x}\mathrm{ln}{x}\right)}{{x}\mathrm{ln}{x}}−\mathrm{2}\frac{{d}\left(\mathrm{ln}{x}\right)}{\mathrm{ln}{x}}\right) \\ $$$$\mathrm{I}\:=\:\left[\mathrm{ln}\left({x}\mathrm{ln}{x}\right)−\mathrm{2ln}\left(\mathrm{ln}{x}\right)\right]_{{e}^{\mathrm{2}} } ^{{e}^{\mathrm{3}} } \\ $$$$\mathrm{I}\:=\:\left[\mathrm{ln}\left(\frac{{x}}{\mathrm{ln}{x}}\right)\right]_{{e}^{\mathrm{2}} } ^{{e}^{\mathrm{3}} } \\ $$$$\mathrm{I}\:=\:\mathrm{ln}\left(\frac{{e}^{\mathrm{3}} }{\mathrm{3}}\right)−\mathrm{ln}\left(\frac{{e}^{\mathrm{2}} }{\mathrm{2}}\right)\:=\:\mathrm{ln}\left(\frac{\mathrm{2}{e}}{\mathrm{3}}\right)\:=\:\mathrm{1}+\mathrm{ln}\frac{\mathrm{2}}{\mathrm{3}} \\ $$
