Question Number 131470 by bemath last updated on 05/Feb/21

$${Consider}\:{a}\:{large}\:{tank}\:{holding} \\ $$$$\mathrm{1000}\:{L}\:{of}\:{pure}\:{water}\:{into} \\ $$$${which}\:{a}\:{brine}\:{solution}\:{of} \\ $$$${salt}\:{begins}\:{to}\:{flow}\:{at}\:{constant} \\ $$$${rate}\:{of}\:\mathrm{6}{L}/{min}.\:{The}\:{solution} \\ $$$${inside}\:{the}\:{tank}\:{is}\:{kept}\:{well} \\ $$$${stirred}\:{and}\:{is}\:{flowing}\:{out}\:{of} \\ $$$${the}\:{tank}\:{at}\:{rate}\:{of}\:\mathrm{6}{L}/{min}. \\ $$$${If}\:{the}\:{concentration}\:{of}\:{salt} \\ $$$${in}\:{the}\:{brine}\:{entering}\:{the}\:{tank} \\ $$$${is}\:\mathrm{0}.\mathrm{1}\:{kg}/{L},\:{determine}\:{when} \\ $$$${the}\:{co}\mathrm{n}{centration}\:{of}\:{salt} \\ $$$${in}\:{the}\:{tank}\:{will}\:{reach}\:\mathrm{0}.\mathrm{05}\:{kg}/{L} \\ $$$$ \\ $$
Commented by bemath last updated on 05/Feb/21

$$\mathrm{thank}\:\mathrm{all}\:\mathrm{master} \\ $$
Answered by EDWIN88 last updated on 05/Feb/21
![we conclude that the input rate of salt into the tank is (6L/min)×(0.1 kg/min)=0.6 kg/min out put rate of salt is (6L/min) [ ((x(t))/(1000)) kg/L ] = ((3x(t))/(500)) kg/min where x(t) denote the mass of salt in tank at time t ⇔ (dx/dt) = 0.6−((3x)/(500)) ; x(0)=0 ⇔ (dx/(100−x)) = (3/(500)) dt ; ln ∣100−x∣=−(3/(500))t+c ⇔100−x(t)=λe^(−(3/(500))t) ; t=0 ;x(0)=0 ⇒ 100=λ ; 100−x(t)=100e^(−(3/(500)) t) ⇔x(t) = 100(1−e^(−((3t)/(500))) ) ((x(t))/(1000)) = 0.1(1−e^(−((3t)/(500))) ) kg/L to determine when the concentration of salt is 0.05 kg/L this gives 0.1(1−e^(−((3t)/(500))) )= 0.05 ; e^(−((3t)/(500))) = 0.5 t = ((500.ln 2)/3) ≈ 115.52 min](https://www.tinkutara.com/question/Q131476.png)
$$\mathrm{we}\:\mathrm{conclude}\:\mathrm{that}\:\mathrm{the}\:\mathrm{input}\:\mathrm{rate}\:\mathrm{of}\:\mathrm{salt}\:\mathrm{into} \\ $$$$\mathrm{the}\:\mathrm{tank}\:\mathrm{is}\:\left(\mathrm{6L}/\mathrm{min}\right)×\left(\mathrm{0}.\mathrm{1}\:\mathrm{kg}/\mathrm{min}\right)=\mathrm{0}.\mathrm{6}\:\mathrm{kg}/\mathrm{min} \\ $$$$\mathrm{out}\:\mathrm{put}\:\mathrm{rate}\:\mathrm{of}\:\mathrm{salt}\:\mathrm{is}\:\left(\mathrm{6L}/\mathrm{min}\right)\:\left[\:\frac{\mathrm{x}\left(\mathrm{t}\right)}{\mathrm{1000}}\:\mathrm{kg}/\mathrm{L}\:\right]\:=\:\frac{\mathrm{3x}\left(\mathrm{t}\right)}{\mathrm{500}}\:\mathrm{kg}/\mathrm{min} \\ $$$$\mathrm{where}\:\mathrm{x}\left(\mathrm{t}\right)\:\mathrm{denote}\:\mathrm{the}\:\mathrm{mass}\:\mathrm{of}\:\mathrm{salt}\:\mathrm{in}\:\mathrm{tank}\:\mathrm{at}\:\mathrm{time}\:\mathrm{t} \\ $$$$\Leftrightarrow\:\frac{\mathrm{dx}}{\mathrm{dt}}\:=\:\mathrm{0}.\mathrm{6}−\frac{\mathrm{3x}}{\mathrm{500}}\:;\:\mathrm{x}\left(\mathrm{0}\right)=\mathrm{0} \\ $$$$\:\Leftrightarrow\:\frac{\mathrm{dx}}{\mathrm{100}−\mathrm{x}}\:=\:\frac{\mathrm{3}}{\mathrm{500}}\:\mathrm{dt}\:;\:\mathrm{ln}\:\mid\mathrm{100}−\mathrm{x}\mid=−\frac{\mathrm{3}}{\mathrm{500}}\mathrm{t}+\mathrm{c} \\ $$$$\Leftrightarrow\mathrm{100}−\mathrm{x}\left(\mathrm{t}\right)=\lambda\mathrm{e}^{−\frac{\mathrm{3}}{\mathrm{500}}\mathrm{t}} \:;\:\mathrm{t}=\mathrm{0}\:;\mathrm{x}\left(\mathrm{0}\right)=\mathrm{0} \\ $$$$\Rightarrow\:\mathrm{100}=\lambda\:;\:\mathrm{100}−\mathrm{x}\left(\mathrm{t}\right)=\mathrm{100e}^{−\frac{\mathrm{3}}{\mathrm{500}}\:\mathrm{t}} \\ $$$$\Leftrightarrow\mathrm{x}\left(\mathrm{t}\right)\:=\:\mathrm{100}\left(\mathrm{1}−\mathrm{e}^{−\frac{\mathrm{3t}}{\mathrm{500}}} \:\right) \\ $$$$\:\frac{\mathrm{x}\left(\mathrm{t}\right)}{\mathrm{1000}}\:=\:\mathrm{0}.\mathrm{1}\left(\mathrm{1}−\mathrm{e}^{−\frac{\mathrm{3t}}{\mathrm{500}}} \:\right)\:\mathrm{kg}/\mathrm{L} \\ $$$$\:\mathrm{to}\:\mathrm{determine}\:\mathrm{when}\:\mathrm{the}\:\mathrm{concentration}\:\mathrm{of} \\ $$$$\mathrm{salt}\:\mathrm{is}\:\mathrm{0}.\mathrm{05}\:\mathrm{kg}/\mathrm{L}\:\:\mathrm{this}\:\mathrm{gives}\: \\ $$$$\:\mathrm{0}.\mathrm{1}\left(\mathrm{1}−\mathrm{e}^{−\frac{\mathrm{3t}}{\mathrm{500}}} \:\right)=\:\mathrm{0}.\mathrm{05}\:;\:\mathrm{e}^{−\frac{\mathrm{3t}}{\mathrm{500}}} \:=\:\mathrm{0}.\mathrm{5} \\ $$$$\:\mathrm{t}\:=\:\frac{\mathrm{500}.\mathrm{ln}\:\mathrm{2}}{\mathrm{3}}\:\approx\:\mathrm{115}.\mathrm{52}\:\mathrm{min} \\ $$
Answered by mr W last updated on 05/Feb/21
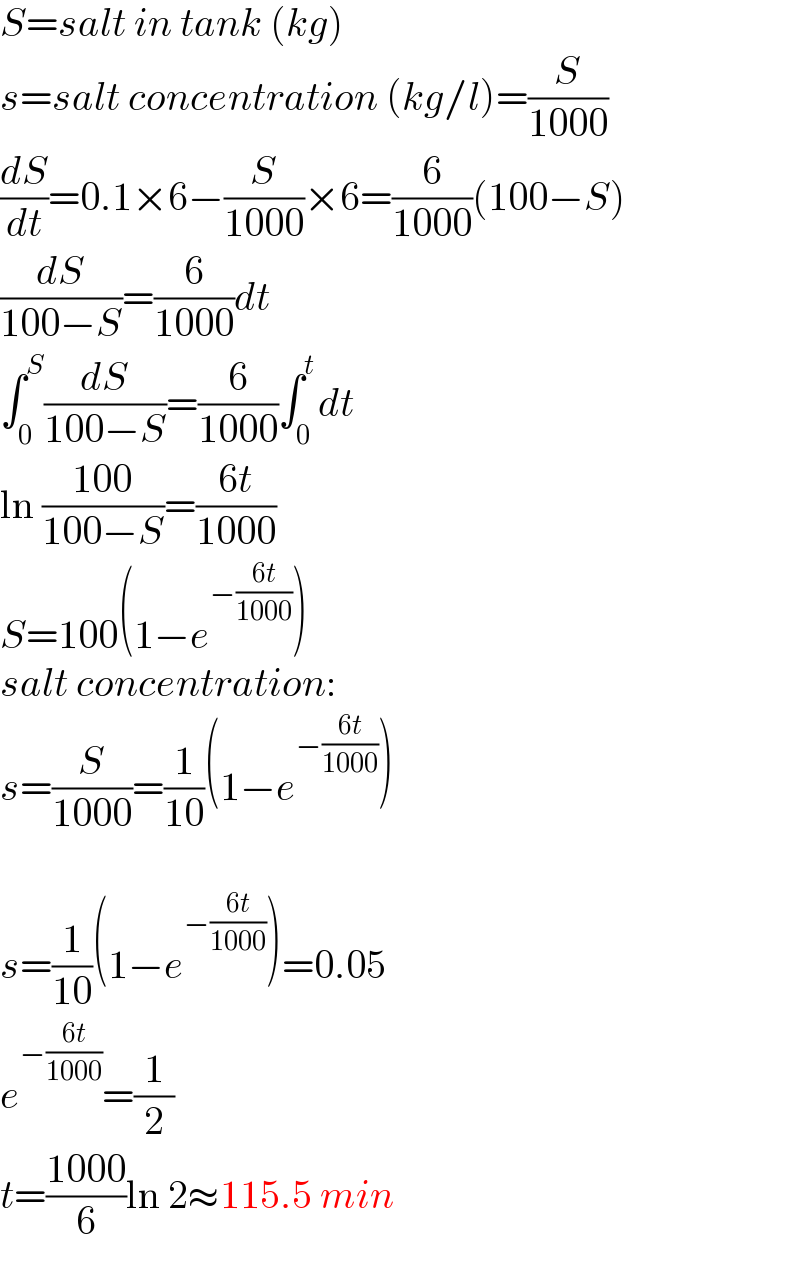
$${S}={salt}\:{in}\:{tank}\:\left({kg}\right) \\ $$$${s}={salt}\:{concentration}\:\left({kg}/{l}\right)=\frac{{S}}{\mathrm{1000}} \\ $$$$\frac{{dS}}{{dt}}=\mathrm{0}.\mathrm{1}×\mathrm{6}−\frac{{S}}{\mathrm{1000}}×\mathrm{6}=\frac{\mathrm{6}}{\mathrm{1000}}\left(\mathrm{100}−{S}\right) \\ $$$$\frac{{dS}}{\mathrm{100}−{S}}=\frac{\mathrm{6}}{\mathrm{1000}}{dt} \\ $$$$\int_{\mathrm{0}} ^{{S}} \frac{{dS}}{\mathrm{100}−{S}}=\frac{\mathrm{6}}{\mathrm{1000}}\int_{\mathrm{0}} ^{{t}} {dt} \\ $$$$\mathrm{ln}\:\frac{\mathrm{100}}{\mathrm{100}−{S}}=\frac{\mathrm{6}{t}}{\mathrm{1000}} \\ $$$${S}=\mathrm{100}\left(\mathrm{1}−{e}^{−\frac{\mathrm{6}{t}}{\mathrm{1000}}} \right) \\ $$$${salt}\:{concentration}: \\ $$$${s}=\frac{{S}}{\mathrm{1000}}=\frac{\mathrm{1}}{\mathrm{10}}\left(\mathrm{1}−{e}^{−\frac{\mathrm{6}{t}}{\mathrm{1000}}} \right) \\ $$$$ \\ $$$${s}=\frac{\mathrm{1}}{\mathrm{10}}\left(\mathrm{1}−{e}^{−\frac{\mathrm{6}{t}}{\mathrm{1000}}} \right)=\mathrm{0}.\mathrm{05} \\ $$$${e}^{−\frac{\mathrm{6}{t}}{\mathrm{1000}}} =\frac{\mathrm{1}}{\mathrm{2}} \\ $$$${t}=\frac{\mathrm{1000}}{\mathrm{6}}\mathrm{ln}\:\mathrm{2}\approx\mathrm{115}.\mathrm{5}\:{min} \\ $$
Answered by TheSupreme last updated on 05/Feb/21
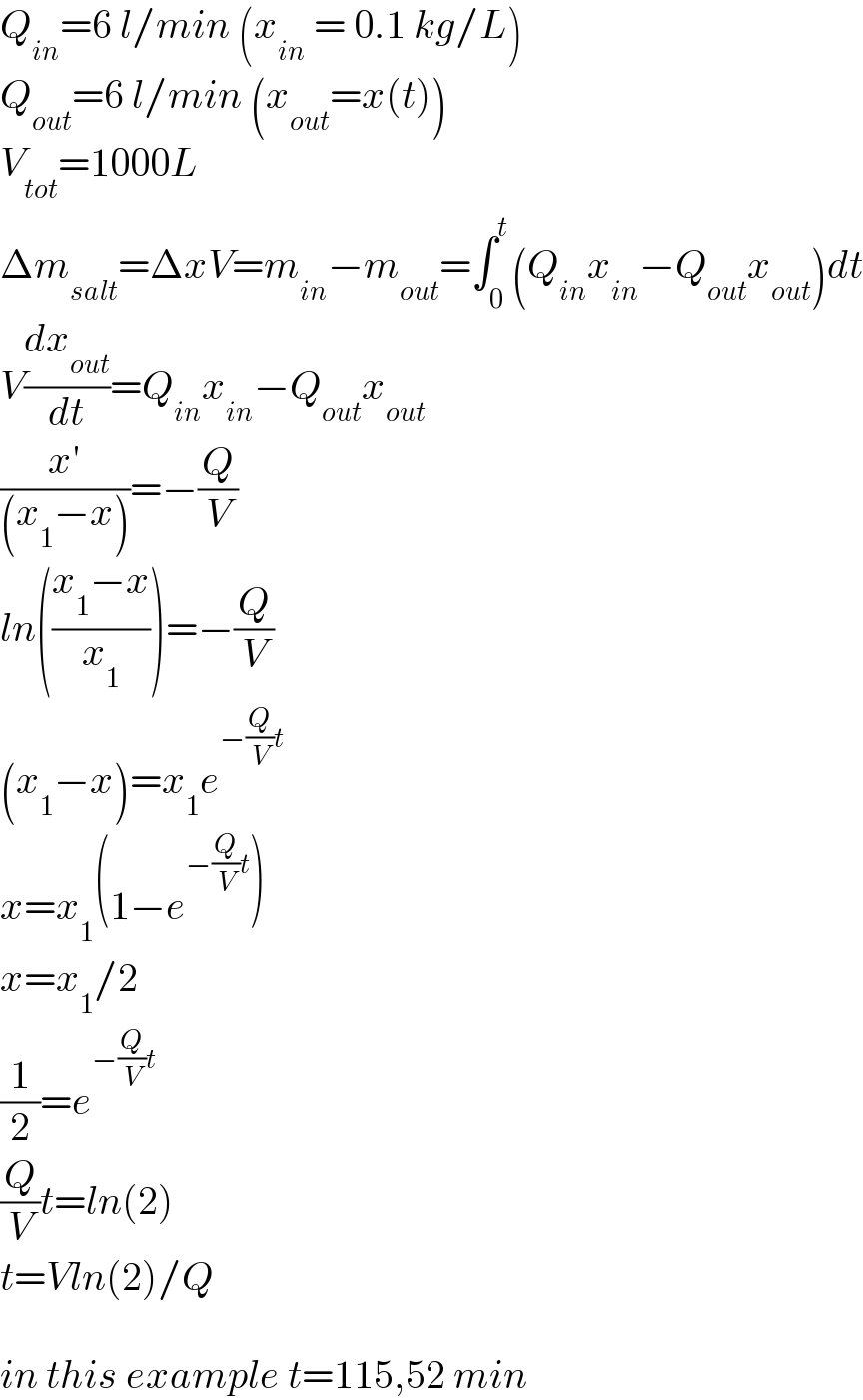
$${Q}_{{in}} =\mathrm{6}\:{l}/{min}\:\left({x}_{{in}} \:=\:\mathrm{0}.\mathrm{1}\:{kg}/{L}\right) \\ $$$${Q}_{{out}} =\mathrm{6}\:{l}/{min}\:\left({x}_{{out}} ={x}\left({t}\right)\right) \\ $$$${V}_{{tot}} =\mathrm{1000}{L} \\ $$$$\Delta{m}_{{salt}} =\Delta{xV}={m}_{{in}} −{m}_{{out}} =\int_{\mathrm{0}} ^{{t}} \left({Q}_{{in}} {x}_{{in}} −{Q}_{{out}} {x}_{{out}} \right){dt} \\ $$$${V}\frac{{dx}_{{out}} }{{dt}}={Q}_{{in}} {x}_{{in}} −{Q}_{{out}} {x}_{{out}} \\ $$$$\frac{{x}'}{\left({x}_{\mathrm{1}} −{x}\right)}=−\frac{{Q}}{{V}} \\ $$$${ln}\left(\frac{{x}_{\mathrm{1}} −{x}}{{x}_{\mathrm{1}} }\right)=−\frac{{Q}}{{V}} \\ $$$$\left({x}_{\mathrm{1}} −{x}\right)={x}_{\mathrm{1}} {e}^{−\frac{{Q}}{{V}}{t}} \\ $$$${x}={x}_{\mathrm{1}} \left(\mathrm{1}−{e}^{−\frac{{Q}}{{V}}{t}} \right) \\ $$$${x}={x}_{\mathrm{1}} /\mathrm{2} \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}={e}^{−\frac{{Q}}{{V}}{t}} \\ $$$$\frac{{Q}}{{V}}{t}={ln}\left(\mathrm{2}\right) \\ $$$${t}={Vln}\left(\mathrm{2}\right)/{Q} \\ $$$$ \\ $$$${in}\:{this}\:{example}\:{t}=\mathrm{115},\mathrm{52}\:{min} \\ $$
