Question Number 48 by surabhi last updated on 25/Jan/15
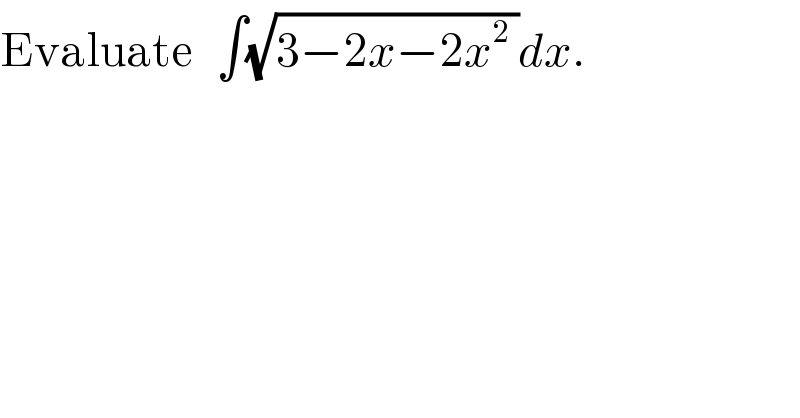
$$\mathrm{Evaluate}\:\:\:\int\sqrt{\mathrm{3}−\mathrm{2}{x}−\mathrm{2}{x}^{\mathrm{2}} \:}{dx}. \\ $$
Answered by surabhi last updated on 04/Nov/14
![∫(√(3−2x−2x^2 )) dx =(√2) ∙ ∫(√(((3/2)−x−x^2 ))) dx =(√2) ∙ ∫(√({(3/2)−(x^2 +x+(1/4))+(1/4)})) dx =(√(2 ))∫ (√({(((√7)/2))^2 − (x+(1/2))^2 } ))dx =(√2)∙[(1/2)(x+(1/2)) (√((3/2)−x−x^2 ))+(1/2)∙(7/4)sin^(−1) {(((x+(1/2)))/( (√7)/2))}]+C =(1/4)(2x+1)(√(3−2x−2x^2 ))+(7/(4(√2)))sin^(−1) (((2x+1)/( (√7))))+C](https://www.tinkutara.com/question/Q49.png)
$$\int\sqrt{\mathrm{3}−\mathrm{2}{x}−\mathrm{2}{x}^{\mathrm{2}} }\:{dx} \\ $$$$=\sqrt{\mathrm{2}}\:\centerdot\:\int\sqrt{\left(\frac{\mathrm{3}}{\mathrm{2}}−{x}−{x}^{\mathrm{2}} \right)}\:{dx} \\ $$$$=\sqrt{\mathrm{2}}\:\centerdot\:\int\sqrt{\left\{\frac{\mathrm{3}}{\mathrm{2}}−\left({x}^{\mathrm{2}} +{x}+\frac{\mathrm{1}}{\mathrm{4}}\right)+\frac{\mathrm{1}}{\mathrm{4}}\right\}}\:{dx} \\ $$$$=\sqrt{\mathrm{2}\:}\int\:\sqrt{\left\{\left(\frac{\sqrt{\mathrm{7}}}{\mathrm{2}}\right)^{\mathrm{2}} \:−\:\left({x}+\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} \:\right\}\:}{dx} \\ $$$$=\sqrt{\mathrm{2}}\centerdot\left[\frac{\mathrm{1}}{\mathrm{2}}\left({x}+\frac{\mathrm{1}}{\mathrm{2}}\right)\:\sqrt{\frac{\mathrm{3}}{\mathrm{2}}−{x}−{x}^{\mathrm{2}} }+\frac{\mathrm{1}}{\mathrm{2}}\centerdot\frac{\mathrm{7}}{\mathrm{4}}\mathrm{sin}^{−\mathrm{1}} \left\{\frac{\left({x}+\frac{\mathrm{1}}{\mathrm{2}}\right)}{\:\sqrt{\mathrm{7}}/\mathrm{2}}\right\}\right]+{C} \\ $$$$=\frac{\mathrm{1}}{\mathrm{4}}\left(\mathrm{2}{x}+\mathrm{1}\right)\sqrt{\mathrm{3}−\mathrm{2}{x}−\mathrm{2}{x}^{\mathrm{2}} }+\frac{\mathrm{7}}{\mathrm{4}\sqrt{\mathrm{2}}}\mathrm{sin}^{−\mathrm{1}} \left(\frac{\mathrm{2}{x}+\mathrm{1}}{\:\sqrt{\mathrm{7}}}\right)+{C} \\ $$
