EvAluate-x-2-9-9-dx-

Question Number 11616 by Nayon last updated on 29/Mar/17

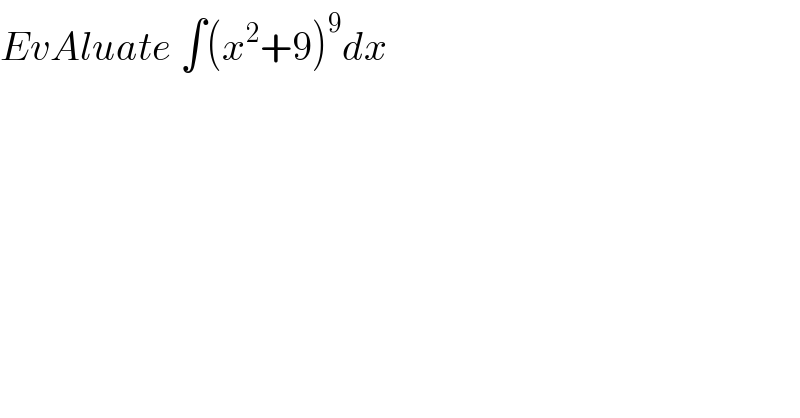
$${EvAluate}\:\int\left({x}^{\mathrm{2}} +\mathrm{9}\right)^{\mathrm{9}} {dx} \\ $$

Answered by Joel576 last updated on 29/Mar/17

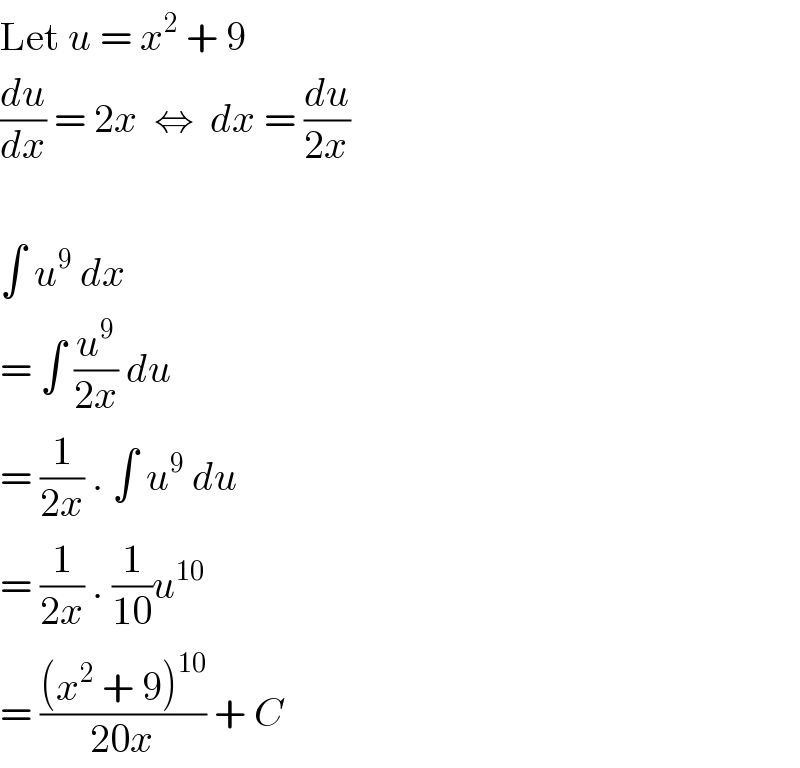
Let u = x^2 + 9 (du/dx) = 2x ⇔ dx = (du/(2x)) ∫ u^9 dx = ∫ (u^9 /(2x)) du = (1/(2x)) . ∫ u^9 du = (1/(2x)) . (1/(10))u^(10) = (((x^2 + 9)^(10) )/(20x)) + C

$$\mathrm{Let}\:{u}\:=\:{x}^{\mathrm{2}} \:+\:\mathrm{9} \\ $$$$\frac{{du}}{{dx}}\:=\:\mathrm{2}{x}\:\:\Leftrightarrow\:\:{dx}\:=\:\frac{{du}}{\mathrm{2}{x}}\:\: \\ $$$$ \\ $$$$\int\:{u}^{\mathrm{9}} \:{dx} \\ $$$$=\:\int\:\frac{{u}^{\mathrm{9}} }{\mathrm{2}{x}}\:{du} \\ $$$$=\:\frac{\mathrm{1}}{\mathrm{2}{x}}\:.\:\int\:{u}^{\mathrm{9}} \:{du} \\ $$$$=\:\frac{\mathrm{1}}{\mathrm{2}{x}}\:.\:\frac{\mathrm{1}}{\mathrm{10}}{u}^{\mathrm{10}} \\ $$$$=\:\frac{\left({x}^{\mathrm{2}} \:+\:\mathrm{9}\right)^{\mathrm{10}} }{\mathrm{20}{x}}\:+\:{C} \\ $$

Commented by Nayon last updated on 29/Mar/17

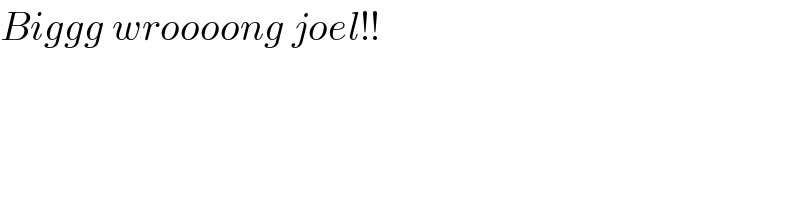
$${Biggg}\:{wroooong}\:{joel}!! \\ $$$$ \\ $$

Commented by Nayon last updated on 29/Mar/17

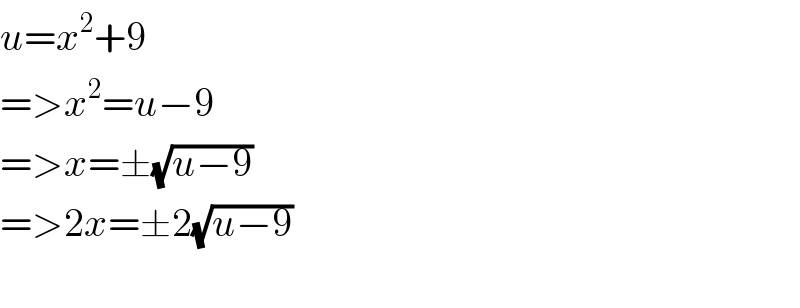
u=x^2 +9 =>x^2 =u−9 =>x=±(√(u−9)) =>2x=±2(√(u−9))

$${u}={x}^{\mathrm{2}} +\mathrm{9} \\ $$$$=>{x}^{\mathrm{2}} ={u}−\mathrm{9} \\ $$$$=>{x}=\pm\sqrt{{u}−\mathrm{9}} \\ $$$$=>\mathrm{2}{x}=\pm\mathrm{2}\sqrt{{u}−\mathrm{9}} \\ $$$$ \\ $$

Commented by linkelly0615 last updated on 29/Mar/17

... uh... (d/dx)[(((x^2 +9)^(10) )/(20x))]≠(x^2 +9)^9

$$… \\ $$$${uh}… \\ $$$$\frac{{d}}{{dx}}\left[\frac{\left({x}^{\mathrm{2}} +\mathrm{9}\right)^{\mathrm{10}} }{\mathrm{20}{x}}\right]\neq\left({x}^{\mathrm{2}} +\mathrm{9}\right)^{\mathrm{9}} \\ $$

Commented by Nayon last updated on 29/Mar/17

$${I}\:{need}\:{it}'{s}\:{ans}.\:{urgently}\:{pls}\:{help} \\ $$$${me}…… \\ $$$$ \\ $$

Answered by linkelly0615 last updated on 29/Mar/17

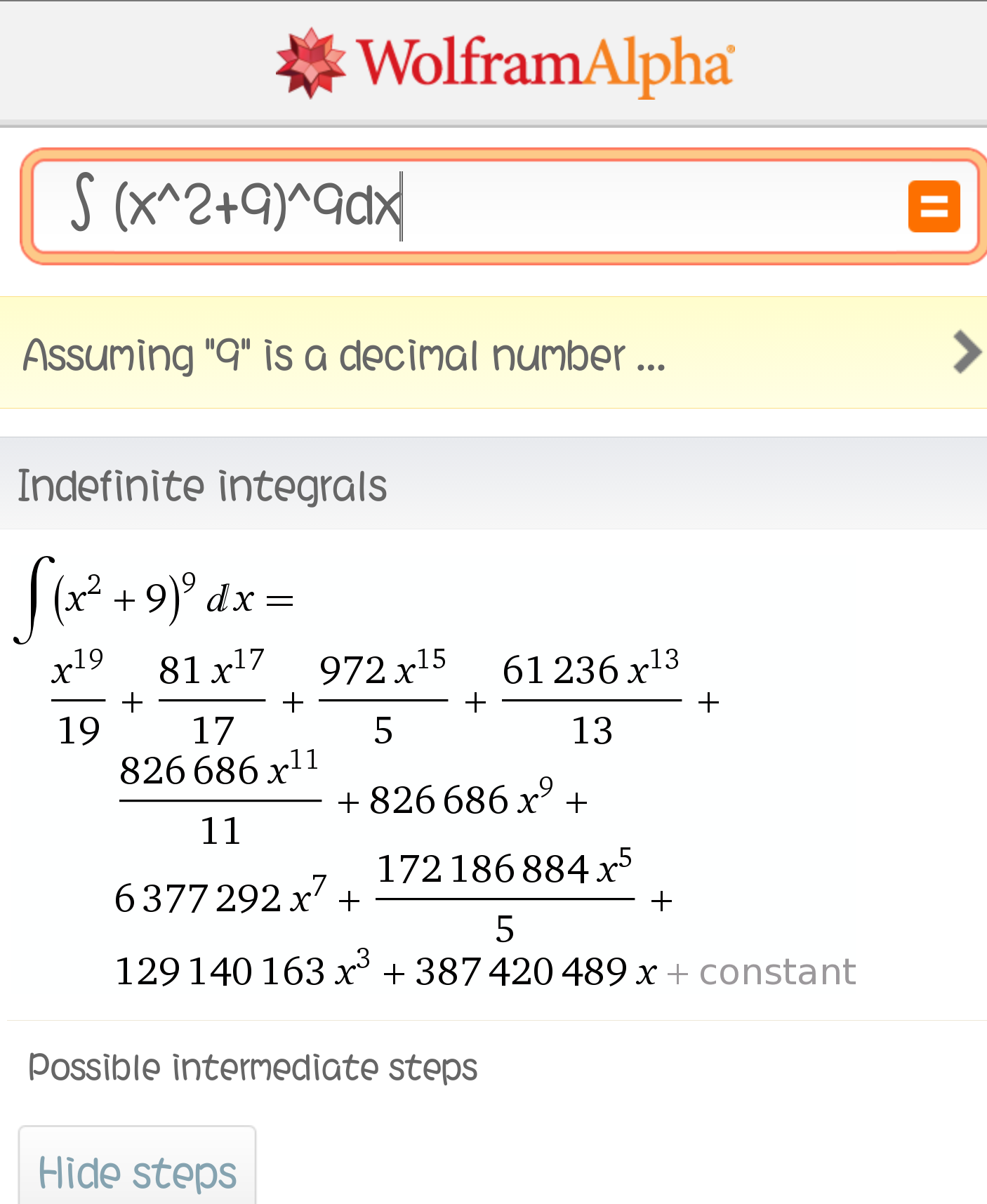
Commented by linkelly0615 last updated on 29/Mar/17

$${I}\:{thik}\:{it}\:{does}\:{not}\:{have}\:{a}\:{simplied} \\ $$$${answer}. \\ $$

Commented by Joel576 last updated on 29/Mar/17

maybe u can expand it with Newton′s binomial and integrated it manually

$$\mathrm{maybe}\:\mathrm{u}\:\mathrm{can}\:\mathrm{expand}\:\mathrm{it}\:\mathrm{with}\:\mathrm{Newton}'\mathrm{s}\:\mathrm{binomial} \\ $$$$\mathrm{and}\:\mathrm{integrated}\:\mathrm{it}\:\mathrm{manually} \\ $$

Answered by mrW1 last updated on 29/Mar/17

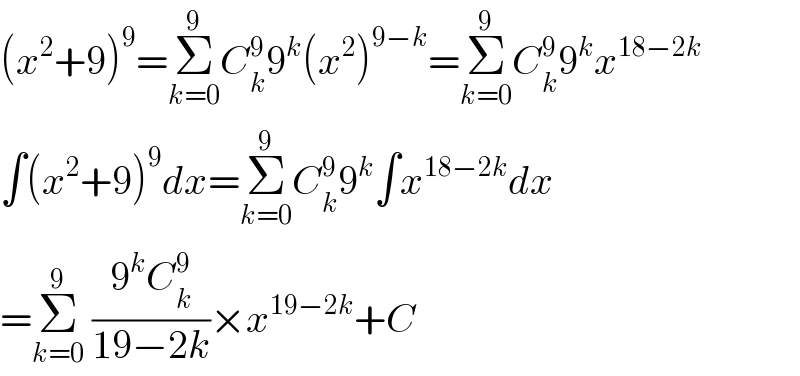
(x^2 +9)^9 =Σ_(k=0) ^9 C_k ^9 9^k (x^2 )^(9−k) =Σ_(k=0) ^9 C_k ^9 9^k x^(18−2k) ∫(x^2 +9)^9 dx=Σ_(k=0) ^9 C_k ^9 9^k ∫x^(18−2k) dx =Σ_(k=0) ^9 ((9^k C_k ^9 )/(19−2k))×x^(19−2k) +C

$$\left({x}^{\mathrm{2}} +\mathrm{9}\right)^{\mathrm{9}} =\underset{{k}=\mathrm{0}} {\overset{\mathrm{9}} {\sum}}{C}_{{k}} ^{\mathrm{9}} \mathrm{9}^{{k}} \left({x}^{\mathrm{2}} \right)^{\mathrm{9}−{k}} =\underset{{k}=\mathrm{0}} {\overset{\mathrm{9}} {\sum}}{C}_{{k}} ^{\mathrm{9}} \mathrm{9}^{{k}} {x}^{\mathrm{18}−\mathrm{2}{k}} \\ $$$$\int\left({x}^{\mathrm{2}} +\mathrm{9}\right)^{\mathrm{9}} {dx}=\underset{{k}=\mathrm{0}} {\overset{\mathrm{9}} {\sum}}{C}_{{k}} ^{\mathrm{9}} \mathrm{9}^{{k}} \int{x}^{\mathrm{18}−\mathrm{2}{k}} {dx} \\ $$$$=\underset{{k}=\mathrm{0}} {\overset{\mathrm{9}} {\sum}}\:\frac{\mathrm{9}^{{k}} {C}_{{k}} ^{\mathrm{9}} }{\mathrm{19}−\mathrm{2}{k}}×{x}^{\mathrm{19}−\mathrm{2}{k}} +{C} \\ $$

Facebook Tweet Pin

EvAluate-x-2-9-9-dx-

Leave a Reply Cancel reply