Question Number 316 by 123456 last updated on 25/Jan/15
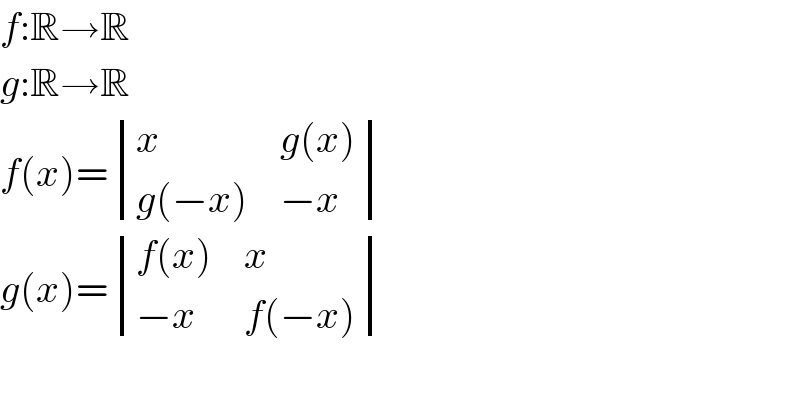
$${f}:\mathbb{R}\rightarrow\mathbb{R} \\ $$$${g}:\mathbb{R}\rightarrow\mathbb{R} \\ $$$${f}\left({x}\right)=\begin{vmatrix}{{x}}&{{g}\left({x}\right)}\\{{g}\left(−{x}\right)}&{−{x}}\end{vmatrix} \\ $$$${g}\left({x}\right)=\begin{vmatrix}{{f}\left({x}\right)}&{{x}}\\{−{x}}&{{f}\left(−{x}\right)}\end{vmatrix} \\ $$
Answered by prakash jain last updated on 21/Dec/14
![f(x)=−x^2 −g(x)g(−x) ...(i) g(x)=f(x)f(−x)+x^2 ...(ii) f(−x)=f(x) g(−x)=g(x) f(x)=−x^2 −[g(x)]^2 g(x)=x^2 +[f(x)]^2 f(x)+g(x)=[f(x)]^2 −[g(x)]^2 =[f(x)+g(x)][f(x)−g(x))] f(x)−g(x)=1 f(x)=1+g(x) 1+g(x)=−x^2 −[g(x)]^2 [g(x)]^2 +g(x)+(1+x^2 )=0 g(x)=((−1±(√(1−4(1+x^2 ))))/2)=((−1±(√(−x^2 −3)))/2) f(x)=1+g(x)=((1±(√(−x^2 −3)))/2) The solution pair meets all condition except f(x) and g(x) are not real for any real x. So given conditons has no solution.](https://www.tinkutara.com/question/Q320.png)
$${f}\left({x}\right)=−{x}^{\mathrm{2}} −{g}\left({x}\right){g}\left(−{x}\right)\:\:\:\:\:…\left({i}\right) \\ $$$${g}\left({x}\right)={f}\left({x}\right){f}\left(−{x}\right)+{x}^{\mathrm{2}} \:\:\:\:\:\:\:\:\:\:…\left({ii}\right) \\ $$$${f}\left(−{x}\right)={f}\left({x}\right) \\ $$$${g}\left(−{x}\right)={g}\left({x}\right) \\ $$$${f}\left({x}\right)=−{x}^{\mathrm{2}} −\left[{g}\left({x}\right)\right]^{\mathrm{2}} \\ $$$${g}\left({x}\right)={x}^{\mathrm{2}} +\left[{f}\left({x}\right)\right]^{\mathrm{2}} \\ $$$$\left.{f}\left({x}\right)+{g}\left({x}\right)=\left[{f}\left({x}\right)\right]^{\mathrm{2}} −\left[{g}\left({x}\right)\right]^{\mathrm{2}} =\left[{f}\left({x}\right)+{g}\left({x}\right)\right]\left[{f}\left({x}\right)−{g}\left({x}\right)\right)\right] \\ $$$${f}\left({x}\right)−{g}\left({x}\right)=\mathrm{1} \\ $$$${f}\left({x}\right)=\mathrm{1}+{g}\left({x}\right) \\ $$$$\mathrm{1}+{g}\left({x}\right)=−{x}^{\mathrm{2}} −\left[{g}\left({x}\right)\right]^{\mathrm{2}} \\ $$$$\left[{g}\left({x}\right)\right]^{\mathrm{2}} +{g}\left({x}\right)+\left(\mathrm{1}+{x}^{\mathrm{2}} \right)=\mathrm{0} \\ $$$${g}\left({x}\right)=\frac{−\mathrm{1}\pm\sqrt{\mathrm{1}−\mathrm{4}\left(\mathrm{1}+{x}^{\mathrm{2}} \right)}}{\mathrm{2}}=\frac{−\mathrm{1}\pm\sqrt{−{x}^{\mathrm{2}} −\mathrm{3}}}{\mathrm{2}} \\ $$$${f}\left({x}\right)=\mathrm{1}+{g}\left({x}\right)=\frac{\mathrm{1}\pm\sqrt{−{x}^{\mathrm{2}} −\mathrm{3}}}{\mathrm{2}} \\ $$$$\mathrm{The}\:\mathrm{solution}\:\mathrm{pair}\:\mathrm{meets}\:\mathrm{all}\:\mathrm{condition}\:\mathrm{except} \\ $$$${f}\left({x}\right)\:\mathrm{and}\:{g}\left({x}\right)\:\mathrm{are}\:\mathrm{not}\:\mathrm{real}\:\mathrm{for}\:\mathrm{any}\:\mathrm{real}\:{x}. \\ $$$$\mathrm{So}\:\mathrm{given}\:\mathrm{conditons}\:\mathrm{has}\:\mathrm{no}\:\mathrm{solution}. \\ $$
