Question Number 650 by 123456 last updated on 19/Feb/15
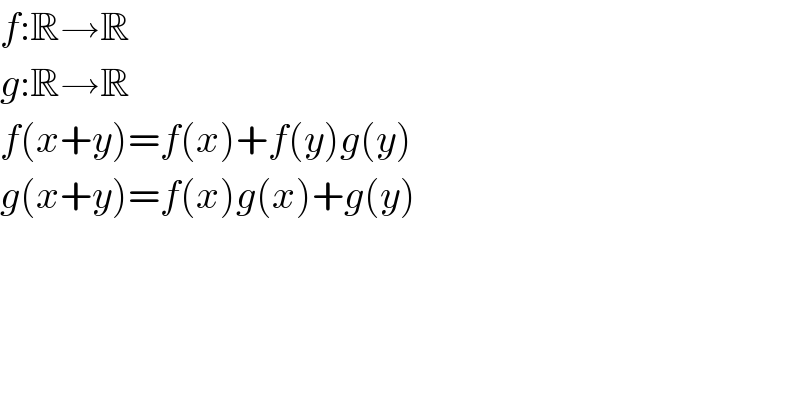
$${f}:\mathbb{R}\rightarrow\mathbb{R} \\ $$$${g}:\mathbb{R}\rightarrow\mathbb{R} \\ $$$${f}\left({x}+{y}\right)={f}\left({x}\right)+{f}\left({y}\right){g}\left({y}\right) \\ $$$${g}\left({x}+{y}\right)={f}\left({x}\right){g}\left({x}\right)+{g}\left({y}\right) \\ $$
Answered by prakash jain last updated on 19/Feb/15
![f(x+y)=f(x)+f(y)g(y) f(y+x)=f(y)+f(x)g(x) ....(1) g(x+y)=g(y)+f(x)g(x) ....(2) From (1) and (2) f(x)=g(x) f(0)=f(0)+[f(0)]^2 ⇒f(0)=0 f(x+y)=f(x)+[f(y)]^2 y=x, x=0 f(x)=[f(x)]^2 f(x)=1 or f(x)=0 f(x)=1 does not satisfy f(0)=0 hence f(x)=0](https://www.tinkutara.com/question/Q654.png)
$${f}\left({x}+{y}\right)={f}\left({x}\right)+{f}\left({y}\right){g}\left({y}\right) \\ $$$${f}\left({y}+{x}\right)={f}\left({y}\right)+{f}\left({x}\right){g}\left({x}\right)\:\:….\left(\mathrm{1}\right) \\ $$$${g}\left({x}+{y}\right)={g}\left({y}\right)+{f}\left({x}\right){g}\left({x}\right)\:\:….\left(\mathrm{2}\right) \\ $$$$\mathrm{From}\:\left(\mathrm{1}\right)\:\mathrm{and}\:\left(\mathrm{2}\right) \\ $$$${f}\left({x}\right)={g}\left({x}\right) \\ $$$${f}\left(\mathrm{0}\right)={f}\left(\mathrm{0}\right)+\left[{f}\left(\mathrm{0}\right)\right]^{\mathrm{2}} \\ $$$$\Rightarrow{f}\left(\mathrm{0}\right)=\mathrm{0} \\ $$$${f}\left({x}+{y}\right)={f}\left({x}\right)+\left[{f}\left({y}\right)\right]^{\mathrm{2}} \\ $$$${y}={x},\:{x}=\mathrm{0} \\ $$$${f}\left({x}\right)=\left[{f}\left({x}\right)\right]^{\mathrm{2}} \\ $$$${f}\left({x}\right)=\mathrm{1}\:\mathrm{or}\:{f}\left({x}\right)=\mathrm{0} \\ $$$${f}\left({x}\right)=\mathrm{1}\:\mathrm{does}\:\mathrm{not}\:\mathrm{satisfy}\:{f}\left(\mathrm{0}\right)=\mathrm{0} \\ $$$$\mathrm{hence}\:{f}\left({x}\right)=\mathrm{0} \\ $$
