Question Number 66256 by Mikael last updated on 11/Aug/19
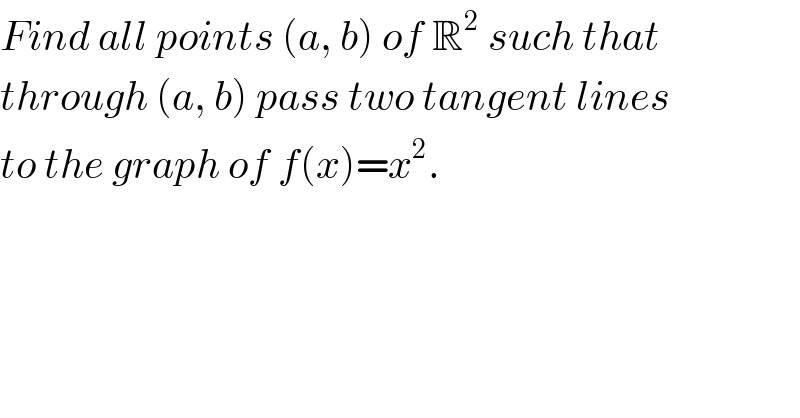
$${Find}\:{all}\:{points}\:\left({a},\:{b}\right)\:{of}\:\mathbb{R}^{\mathrm{2}} \:{such}\:{that}\: \\ $$$${through}\:\left({a},\:{b}\right)\:{pass}\:{two}\:{tangent}\:{lines} \\ $$$${to}\:{the}\:{graph}\:{of}\:{f}\left({x}\right)={x}^{\mathrm{2}} . \\ $$
Commented by kaivan.ahmadi last updated on 11/Aug/19
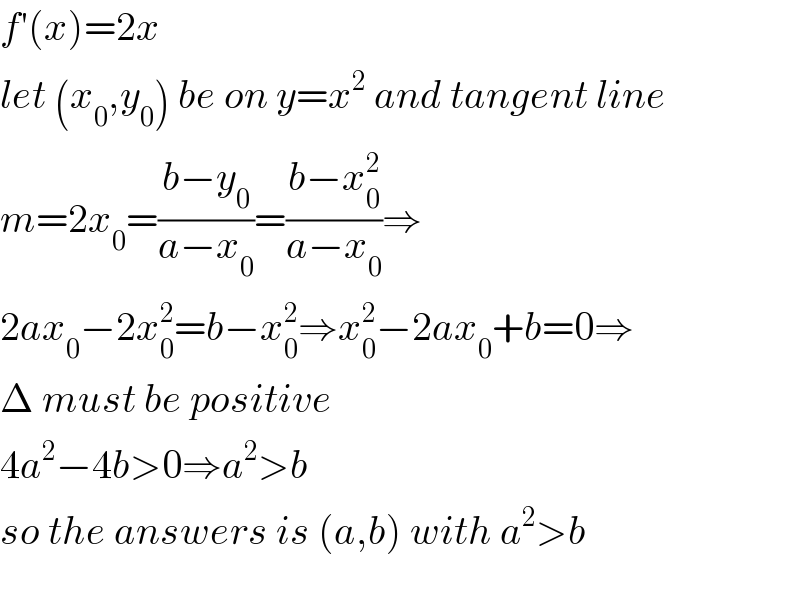
$${f}'\left({x}\right)=\mathrm{2}{x} \\ $$$${let}\:\left({x}_{\mathrm{0}} ,{y}_{\mathrm{0}} \right)\:{be}\:{on}\:{y}={x}^{\mathrm{2}} \:{and}\:{tangent}\:{line} \\ $$$${m}=\mathrm{2}{x}_{\mathrm{0}} =\frac{{b}−{y}_{\mathrm{0}} }{{a}−{x}_{\mathrm{0}} }=\frac{{b}−{x}_{\mathrm{0}} ^{\mathrm{2}} }{{a}−{x}_{\mathrm{0}} }\Rightarrow \\ $$$$\mathrm{2}{ax}_{\mathrm{0}} −\mathrm{2}{x}_{\mathrm{0}} ^{\mathrm{2}} ={b}−{x}_{\mathrm{0}} ^{\mathrm{2}} \Rightarrow{x}_{\mathrm{0}} ^{\mathrm{2}} −\mathrm{2}{ax}_{\mathrm{0}} +{b}=\mathrm{0}\Rightarrow \\ $$$$\Delta\:{must}\:{be}\:{positive} \\ $$$$\mathrm{4}{a}^{\mathrm{2}} −\mathrm{4}{b}>\mathrm{0}\Rightarrow{a}^{\mathrm{2}} >{b} \\ $$$${so}\:{the}\:{answers}\:{is}\:\left({a},{b}\right)\:{with}\:{a}^{\mathrm{2}} >{b} \\ $$$$ \\ $$
Commented by mr W last updated on 12/Aug/19
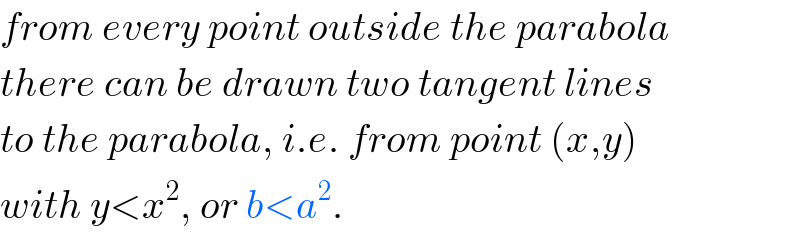
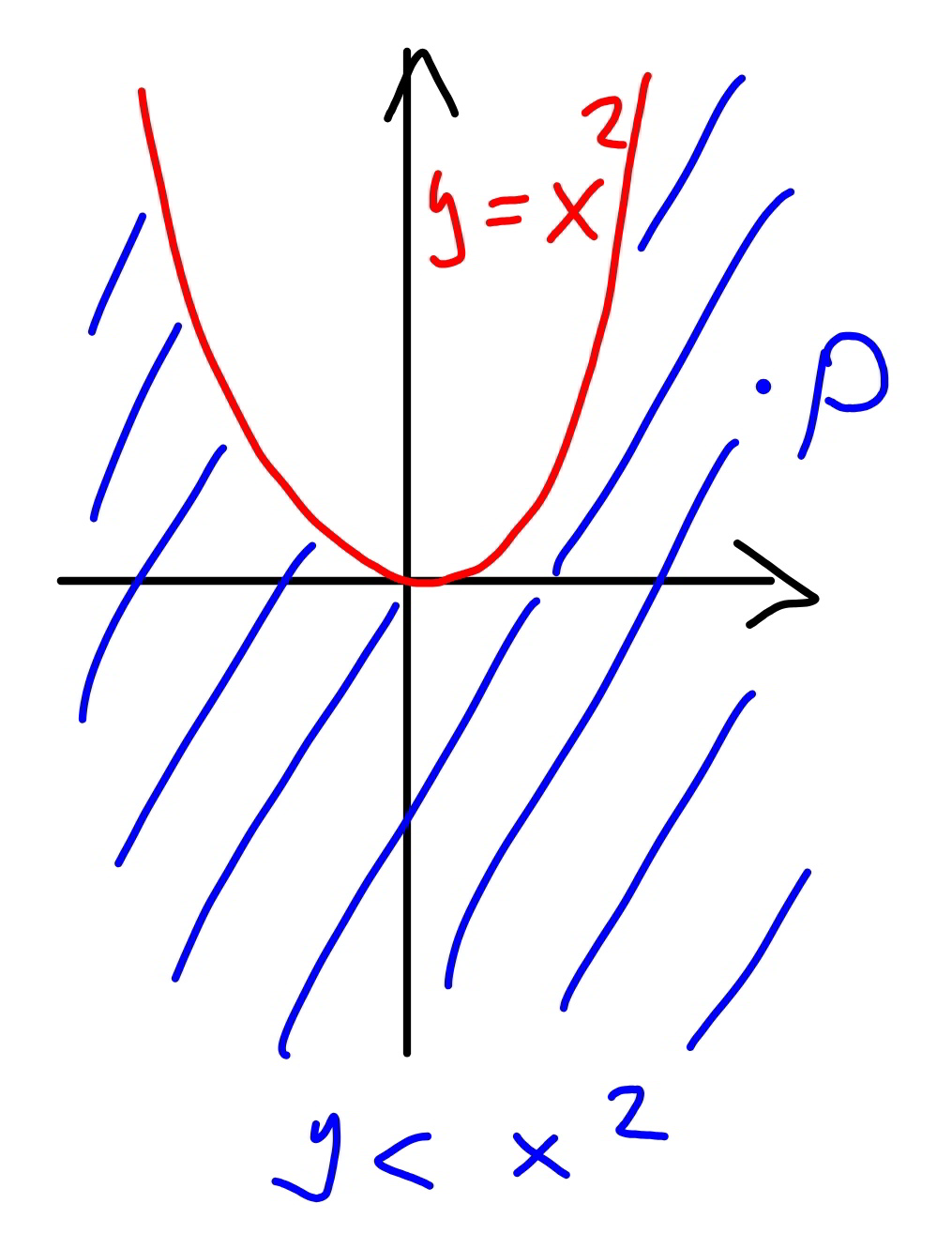
$${from}\:{every}\:{point}\:{outside}\:{the}\:{parabola} \\ $$$${there}\:{can}\:{be}\:{drawn}\:{two}\:{tangent}\:{lines} \\ $$$${to}\:{the}\:{parabola},\:{i}.{e}.\:{from}\:{point}\:\left({x},{y}\right) \\ $$$${with}\:{y}<{x}^{\mathrm{2}} ,\:{or}\:{b}<{a}^{\mathrm{2}} . \\ $$
Commented by mr W last updated on 12/Aug/19
Commented by Mikael last updated on 12/Aug/19

$${thank}\:{you}. \\ $$
Commented by Mikael last updated on 12/Aug/19

$${thank}\:{you}\:{Sir}. \\ $$
Commented by kaivan.ahmadi last updated on 13/Aug/19
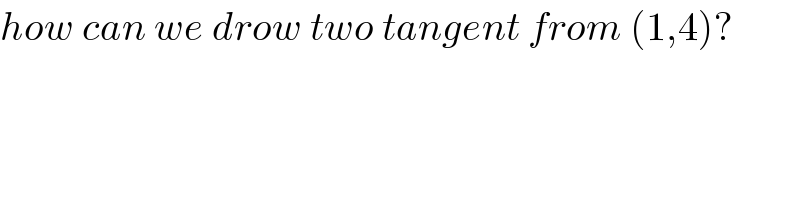
$${how}\:{can}\:{we}\:{drow}\:{two}\:{tangent}\:{from}\:\left(\mathrm{1},\mathrm{4}\right)? \\ $$
Commented by mr W last updated on 14/Aug/19
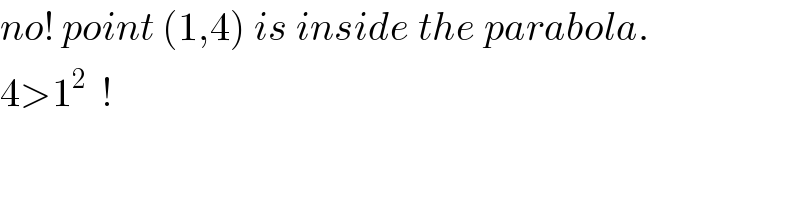
$${no}!\:{point}\:\left(\mathrm{1},\mathrm{4}\right)\:{is}\:{inside}\:{the}\:{parabola}. \\ $$$$\mathrm{4}>\mathrm{1}^{\mathrm{2}} \:\:! \\ $$
