Question Number 2 by user1 last updated on 25/Jan/15
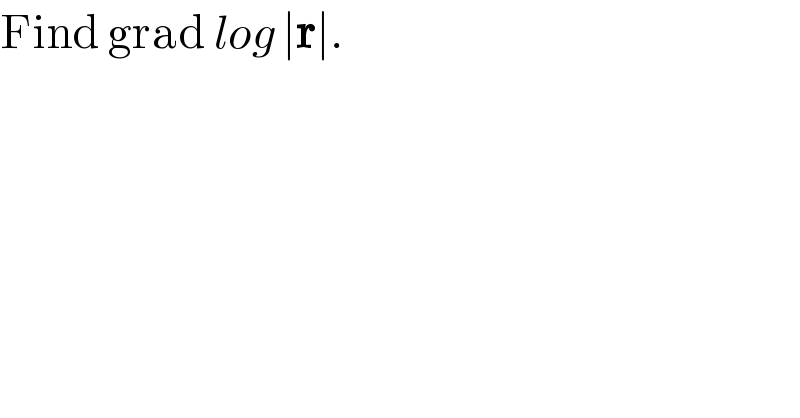
$$\mathrm{Find}\:\mathrm{grad}\:{log}\:\mid\boldsymbol{\mathrm{r}}\mid. \\ $$
Answered by user1 last updated on 29/Oct/14
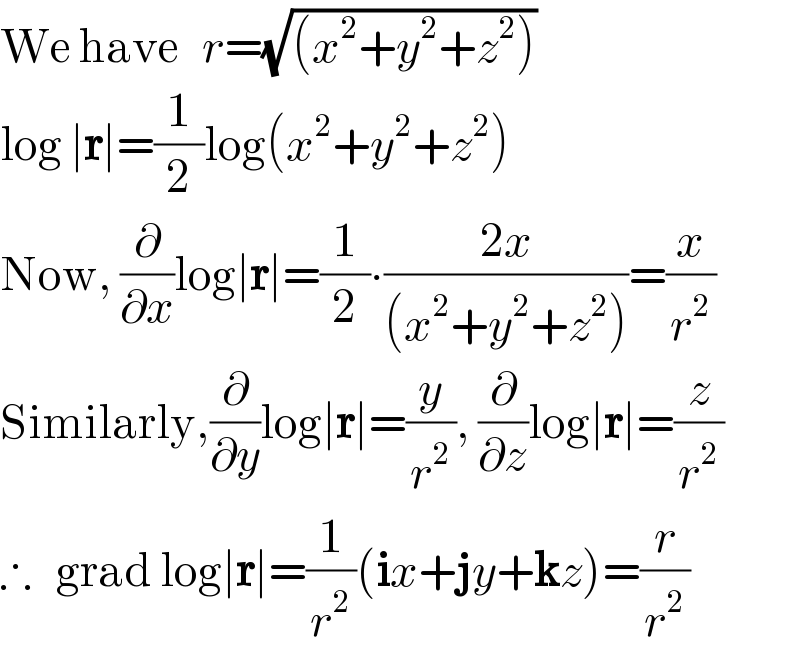
$$\mathrm{We}\:\mathrm{have}\:\:\:{r}=\sqrt{\left({x}^{\mathrm{2}} +{y}^{\mathrm{2}} +{z}^{\mathrm{2}} \right)} \\ $$$$\mathrm{log}\:\mid\boldsymbol{\mathrm{r}}\mid=\frac{\mathrm{1}}{\mathrm{2}}\mathrm{log}\left({x}^{\mathrm{2}} +{y}^{\mathrm{2}} +{z}^{\mathrm{2}} \right) \\ $$$$\mathrm{Now},\:\frac{\partial}{\partial{x}}\mathrm{log}\mid\boldsymbol{\mathrm{r}}\mid=\frac{\mathrm{1}}{\mathrm{2}}\centerdot\frac{\mathrm{2}{x}}{\left({x}^{\mathrm{2}} +{y}^{\mathrm{2}} +{z}^{\mathrm{2}} \right)}=\frac{{x}}{{r}^{\mathrm{2}} } \\ $$$$\mathrm{Similarly},\frac{\partial}{\partial{y}}\mathrm{log}\mid\boldsymbol{\mathrm{r}}\mid=\frac{{y}}{{r}^{\mathrm{2}} },\:\frac{\partial}{\partial{z}}\mathrm{log}\mid\boldsymbol{\mathrm{r}}\mid=\frac{{z}}{{r}^{\mathrm{2}} } \\ $$$$\therefore\:\:\:\mathrm{grad}\:\mathrm{log}\mid\boldsymbol{\mathrm{r}}\mid=\frac{\mathrm{1}}{{r}^{\mathrm{2}} }\left(\boldsymbol{\mathrm{i}}{x}+\boldsymbol{\mathrm{j}}{y}+\boldsymbol{\mathrm{k}}{z}\right)=\frac{{r}}{{r}^{\mathrm{2}} } \\ $$
Commented by SWPlaysMC last updated on 16/Dec/21

$$\mathrm{Ahh}\:\mathrm{yes},\:\mathrm{the}\:\mathrm{first}\:\mathrm{question}\:\mathrm{ever}\:\mathrm{asked}\:\mathrm{on}\:\mathrm{this}\:\mathrm{app}… \\ $$$$\mathrm{What}\:\mathrm{happened}\:\mathrm{to}\:\mathrm{question}\:\mathrm{ID}\:\mathrm{1}?\:\mathrm{Did}\:\mathrm{it}\:\mathrm{EVER}\:\mathrm{exist}? \\ $$$${Edit}:\:{All}\:{hail}\:{user}\mathrm{1}! \\ $$
Commented by talminator2856791 last updated on 05/Sep/21

$$\:\mathrm{no}\:\mathrm{clue}. \\ $$
Commented by talminator2856791 last updated on 05/Sep/21

$$\:\mathrm{it}\:\mathrm{appears}\:\mathrm{that}\:\mathrm{user1}\:\mathrm{also}\:\mathrm{doesnt} \\ $$$$\:\mathrm{exist}\:\mathrm{now}. \\ $$
Commented by MathematicalUser2357 last updated on 08/Jan/24

$${BUG} \\ $$
