Question Number 133897 by bemath last updated on 25/Feb/21
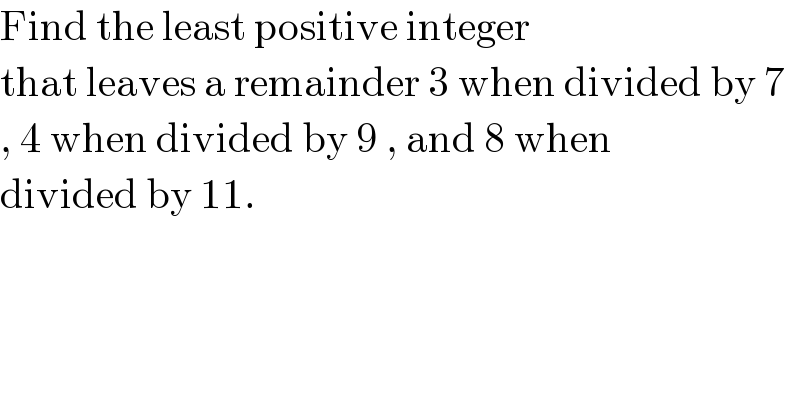
$$\mathrm{Find}\:\mathrm{the}\:\mathrm{least}\:\mathrm{positive}\:\mathrm{integer} \\ $$$$\mathrm{that}\:\mathrm{leaves}\:\mathrm{a}\:\mathrm{remainder}\:\mathrm{3}\:\mathrm{when}\:\mathrm{divided}\:\mathrm{by}\:\mathrm{7} \\ $$$$,\:\mathrm{4}\:\mathrm{when}\:\mathrm{divided}\:\mathrm{by}\:\mathrm{9}\:,\:\mathrm{and}\:\mathrm{8}\:\mathrm{when} \\ $$$$\mathrm{divided}\:\mathrm{by}\:\mathrm{11}. \\ $$
Answered by john_santu last updated on 25/Feb/21

$${by}\:{Use}\:{Chinese}\:{Remainder}\:{theorem}\: \\ $$$$\begin{array}{|c|c|c|c|}{{i}}&\hline{{n}_{{i}} }&\hline{{N}_{{i}} }&\hline{{y}_{{i}} {N}_{{i}} \equiv\mathrm{1}\:{mod}\:{n}_{\mathrm{1}} }&\hline{{c}_{{i}} }&\hline{{N}_{{i}} {y}_{{i}} {c}_{{i}} }\\{\mathrm{1}}&\hline{\mathrm{7}}&\hline{\mathrm{9}.\mathrm{11}}&\hline{{y}_{\mathrm{1}} .\mathrm{9}.\mathrm{11}\equiv\mathrm{1}\:{mod}\:\mathrm{7}\rightarrow{y}_{\mathrm{1}} =\mathrm{1}}&\hline{\mathrm{3}}&\hline{\mathrm{297}}\\{\mathrm{2}}&\hline{\mathrm{9}}&\hline{\mathrm{7}.\mathrm{11}}&\hline{{y}_{\mathrm{2}} .\mathrm{7}.\mathrm{11}\equiv\mathrm{1}\:{mod}\:\mathrm{9}\rightarrow{y}_{\mathrm{2}} =\mathrm{2}}&\hline{\mathrm{4}}&\hline{\mathrm{616}}\\{\mathrm{3}}&\hline{\mathrm{11}}&\hline{\mathrm{7}.\mathrm{9}}&\hline{{y}_{\mathrm{3}} .\mathrm{7}.\mathrm{9}\equiv\mathrm{1}\:{mod}\:\mathrm{11}\rightarrow{y}_{\mathrm{3}} =\mathrm{7}}&\hline{\mathrm{8}}&\hline{\mathrm{3528}}\\\hline\end{array} \\ $$$$\:{X}\:=\:\sum_{{i}} \:{N}_{{i}} {y}_{{i}} {c}_{{i}} \:=\:\mathrm{4441} \\ $$$${we}\:{have}\:{x}\equiv{X}\:{mod}\:{N}\:\Rightarrow{x}\equiv\:\mathrm{4441}\:\left({mod}\:\mathrm{693}\right) \\ $$$${x}\equiv\:\mathrm{283}\:\left({mod}\:\mathrm{693}\right)\:{or}\:{x}\:=\:\mathrm{693}{k}\:+\:\mathrm{283}\:;\:{k}\in\mathbb{Z} \\ $$$${then}\:{the}\:{least}\:{positive}\:{integer}\:{is}\:{x}\:=\:\mathrm{283}\: \\ $$
Commented by talminator2856791 last updated on 25/Feb/21

$$\:\mathrm{why}\:\mathrm{is}\:\mathrm{it}\:\mathrm{called}\:\mathrm{chinese}\:\mathrm{remainder}\:\mathrm{theorem}? \\ $$
Answered by talminator2856791 last updated on 25/Feb/21
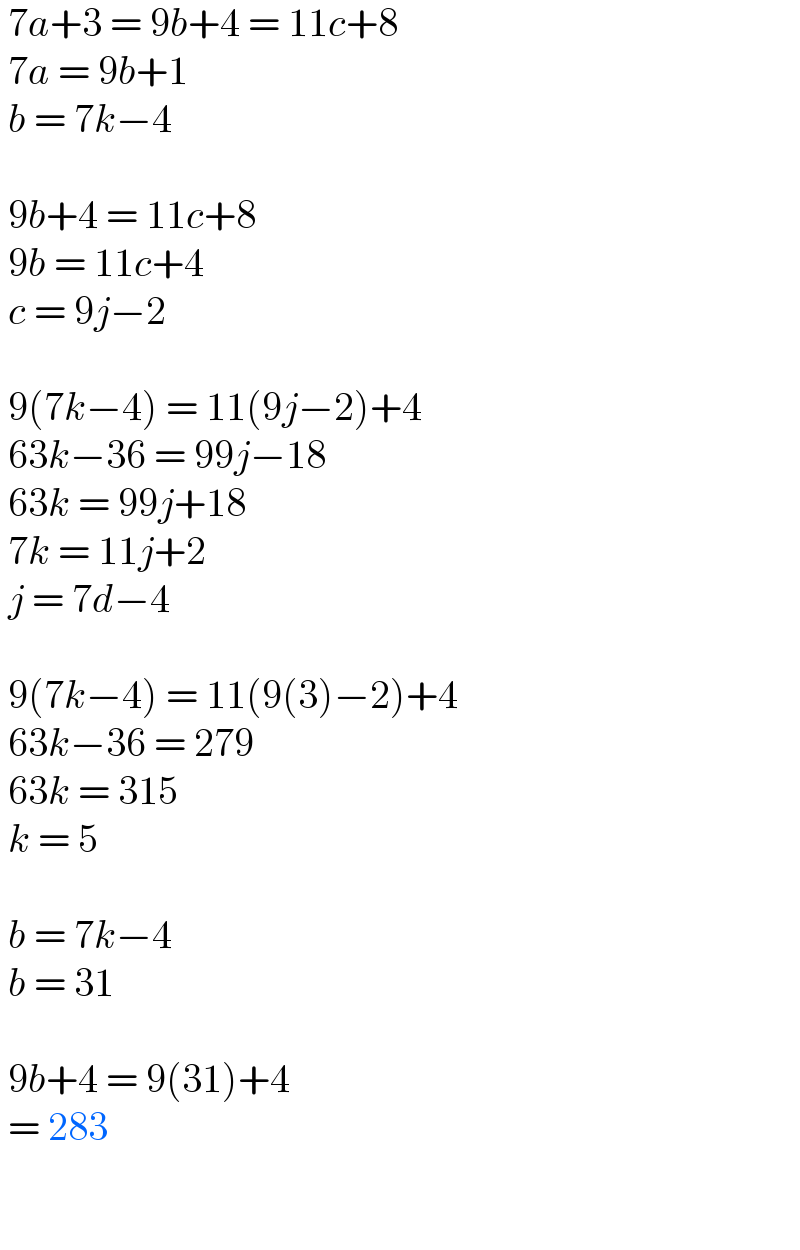
$$\:\mathrm{7}{a}+\mathrm{3}\:=\:\mathrm{9}{b}+\mathrm{4}\:=\:\mathrm{11}{c}+\mathrm{8} \\ $$$$\:\mathrm{7}{a}\:=\:\mathrm{9}{b}+\mathrm{1} \\ $$$$\:{b}\:=\:\mathrm{7}{k}−\mathrm{4} \\ $$$$\: \\ $$$$\:\mathrm{9}{b}+\mathrm{4}\:=\:\mathrm{11}{c}+\mathrm{8} \\ $$$$\:\mathrm{9}{b}\:=\:\mathrm{11}{c}+\mathrm{4} \\ $$$$\:{c}\:=\:\mathrm{9}{j}−\mathrm{2} \\ $$$$\: \\ $$$$\:\mathrm{9}\left(\mathrm{7}{k}−\mathrm{4}\right)\:=\:\mathrm{11}\left(\mathrm{9}{j}−\mathrm{2}\right)+\mathrm{4} \\ $$$$\:\mathrm{63}{k}−\mathrm{36}\:=\:\mathrm{99}{j}−\mathrm{18} \\ $$$$\:\mathrm{63}{k}\:=\:\mathrm{99}{j}+\mathrm{18} \\ $$$$\:\mathrm{7}{k}\:=\:\mathrm{11}{j}+\mathrm{2} \\ $$$$\:{j}\:=\:\mathrm{7}{d}−\mathrm{4} \\ $$$$\: \\ $$$$\:\mathrm{9}\left(\mathrm{7}{k}−\mathrm{4}\right)\:=\:\mathrm{11}\left(\mathrm{9}\left(\mathrm{3}\right)−\mathrm{2}\right)+\mathrm{4} \\ $$$$\:\mathrm{63}{k}−\mathrm{36}\:=\:\mathrm{279} \\ $$$$\:\mathrm{63}{k}\:=\:\mathrm{315} \\ $$$$\:{k}\:=\:\mathrm{5} \\ $$$$\: \\ $$$$\:{b}\:=\:\mathrm{7}{k}−\mathrm{4} \\ $$$$\:{b}\:=\:\mathrm{31} \\ $$$$\: \\ $$$$\:\mathrm{9}{b}+\mathrm{4}\:=\:\mathrm{9}\left(\mathrm{31}\right)+\mathrm{4}\: \\ $$$$\:=\:\mathrm{283} \\ $$$$\: \\ $$
