Question Number 134705 by bramlexs22 last updated on 06/Mar/21
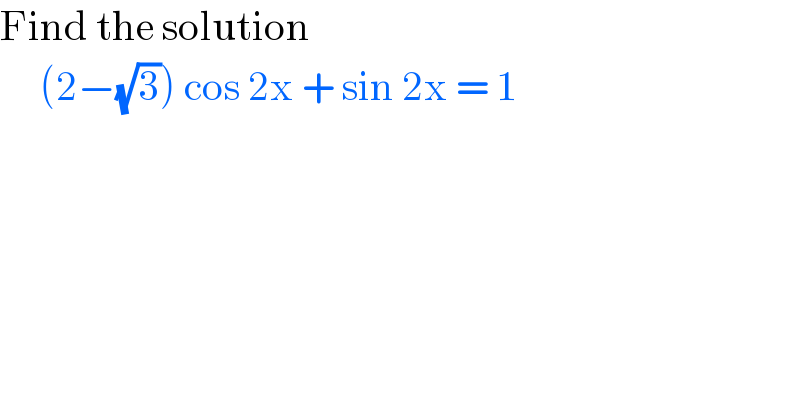
$$\mathrm{Find}\:\mathrm{the}\:\mathrm{solution}\: \\ $$$$\:\:\:\:\:\left(\mathrm{2}−\sqrt{\mathrm{3}}\right)\:\mathrm{cos}\:\mathrm{2x}\:+\:\mathrm{sin}\:\mathrm{2x}\:=\:\mathrm{1} \\ $$
Answered by john_santu last updated on 06/Mar/21

$$\:{We}\:{can}\:{setting}\:\rightarrow\begin{cases}{{X}=\mathrm{cos}\:\mathrm{2}{x}}\\{{Y}=\mathrm{sin}\:\mathrm{2}{x}}\end{cases} \\ $$$${so}\:{the}\:{equation}\:{becomes}\:\begin{cases}{\left(\mathrm{2}−\sqrt{\mathrm{3}}\right){X}+{Y}\:=\:\mathrm{1}}\\{{X}^{\mathrm{2}} +{Y}^{\:\mathrm{2}} \:=\:\mathrm{1}}\end{cases} \\ $$$${substituting}\:{Y}\:=\:\mathrm{1}−\left(\mathrm{2}−\sqrt{\mathrm{3}}\right){X}\:{into} \\ $$$${the}\:{second}\:{equation}\:{gives}\: \\ $$$${X}^{\mathrm{2}} +\mathrm{1}−\mathrm{2}\left(\mathrm{2}−\sqrt{\mathrm{3}}\right){X}+\left(\mathrm{7}−\mathrm{4}\sqrt{\mathrm{3}}\right){X}^{\mathrm{2}} \:=\:\mathrm{1} \\ $$$${which}\:{has}\:{solution}\:{X}=\:\mathrm{0}\:{or}\:{X}=\:\frac{\mathrm{1}}{\mathrm{2}} \\ $$$${for}\:{X}\:=\:\mathrm{0}\:{gives}\:{Y}\:=\:\mathrm{1}\:{and}\:{for}\:{X}=\frac{\mathrm{1}}{\mathrm{2}} \\ $$$${gives}\:{Y}\:=\:\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\:.\:{Now}\:{solve}\:{the}\:{equations} \\ $$$$\begin{cases}{\mathrm{cos}\:\mathrm{2}{x}\:=\:\mathrm{0}}\\{\mathrm{sin}\:\mathrm{2}{x}\:=\:\mathrm{1}}\end{cases}\:{and}\:\begin{cases}{\mathrm{cos}\:\mathrm{2}{x}=\frac{\mathrm{1}}{\mathrm{2}}}\\{\mathrm{sin}\:\mathrm{2}{x}=\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}}\end{cases} \\ $$$${The}\:{solution}\:\begin{cases}{{x}=\frac{\pi}{\mathrm{4}}+{n}\pi}\\{{x}=\:\frac{\pi}{\mathrm{6}}+{n}\pi}\end{cases}\:{n}\in\mathbb{Z} \\ $$
