Question Number 142426 by Mathspace last updated on 31/May/21
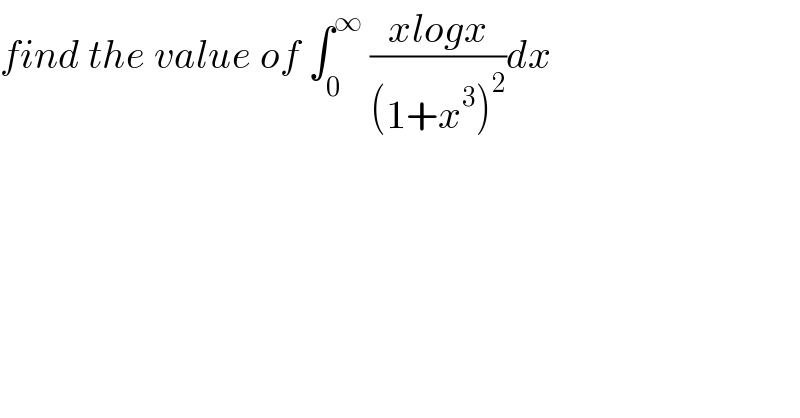
$${find}\:{the}\:{value}\:{of}\:\int_{\mathrm{0}} ^{\infty} \:\frac{{xlogx}}{\left(\mathrm{1}+{x}^{\mathrm{3}} \right)^{\mathrm{2}} }{dx} \\ $$
Answered by mindispower last updated on 01/Jun/21
![x→(1/x) =−∫_0 ^∞ ((x^3 ln(x)dx)/((1+x^3 )^2 )) =−[−((xln(x))/(3(1+x^3 )))]_0 ^∞ +(1/3)∫_0 ^∞ (1/(1+x^3 ))dx+(1/3)∫_0 ^∞ ((ln(x))/(1+x^3 ))dx] −(1/9)∫_0 ^∞ (t^((−2)/3) /(1+t))dt−(1/(27))∫_0 ^∞ ((t^(−(2/3)) ln(t))/(1+t))dt β(x,y)=∫_0 ^∞ (t^(x−1) /((1+t)^(x+y) )) −(1/9)β((1/3),(2/3))−(1/(27))β_x ((1/3),(2/3)) =−((2π)/(9(√3)))−(1/(27))β((1/3),(2/3))(Ψ(1)−Ψ((1/3))) =−((2π)/(9(√3)))(1+(1/3)(−γ+γ+(π/(2(√3)))+(3/2)ln(3)) =−((2π)/(9(√3)))−(π^2 /(81))−((πln(3))/(9(√3)))](https://www.tinkutara.com/question/Q142473.png)
$${x}\rightarrow\frac{\mathrm{1}}{{x}} \\ $$$$=−\int_{\mathrm{0}} ^{\infty} \frac{{x}^{\mathrm{3}} {ln}\left({x}\right){dx}}{\left(\mathrm{1}+{x}^{\mathrm{3}} \right)^{\mathrm{2}} } \\ $$$$\left.=−\left[−\frac{{xln}\left({x}\right)}{\mathrm{3}\left(\mathrm{1}+{x}^{\mathrm{3}} \right)}\right]_{\mathrm{0}} ^{\infty} +\frac{\mathrm{1}}{\mathrm{3}}\int_{\mathrm{0}} ^{\infty} \frac{\mathrm{1}}{\mathrm{1}+{x}^{\mathrm{3}} }{dx}+\frac{\mathrm{1}}{\mathrm{3}}\int_{\mathrm{0}} ^{\infty} \frac{{ln}\left({x}\right)}{\mathrm{1}+{x}^{\mathrm{3}} }{dx}\right] \\ $$$$−\frac{\mathrm{1}}{\mathrm{9}}\int_{\mathrm{0}} ^{\infty} \frac{{t}^{\frac{−\mathrm{2}}{\mathrm{3}}} }{\mathrm{1}+{t}}{dt}−\frac{\mathrm{1}}{\mathrm{27}}\int_{\mathrm{0}} ^{\infty} \frac{{t}^{−\frac{\mathrm{2}}{\mathrm{3}}} {ln}\left({t}\right)}{\mathrm{1}+{t}}{dt} \\ $$$$\beta\left({x},{y}\right)=\int_{\mathrm{0}} ^{\infty} \frac{{t}^{{x}−\mathrm{1}} }{\left(\mathrm{1}+{t}\right)^{{x}+{y}} } \\ $$$$−\frac{\mathrm{1}}{\mathrm{9}}\beta\left(\frac{\mathrm{1}}{\mathrm{3}},\frac{\mathrm{2}}{\mathrm{3}}\right)−\frac{\mathrm{1}}{\mathrm{27}}\beta_{{x}} \left(\frac{\mathrm{1}}{\mathrm{3}},\frac{\mathrm{2}}{\mathrm{3}}\right) \\ $$$$=−\frac{\mathrm{2}\pi}{\mathrm{9}\sqrt{\mathrm{3}}}−\frac{\mathrm{1}}{\mathrm{27}}\beta\left(\frac{\mathrm{1}}{\mathrm{3}},\frac{\mathrm{2}}{\mathrm{3}}\right)\left(\Psi\left(\mathrm{1}\right)−\Psi\left(\frac{\mathrm{1}}{\mathrm{3}}\right)\right) \\ $$$$=−\frac{\mathrm{2}\pi}{\mathrm{9}\sqrt{\mathrm{3}}}\left(\mathrm{1}+\frac{\mathrm{1}}{\mathrm{3}}\left(−\gamma+\gamma+\frac{\pi}{\mathrm{2}\sqrt{\mathrm{3}}}+\frac{\mathrm{3}}{\mathrm{2}}{ln}\left(\mathrm{3}\right)\right)\right. \\ $$$$=−\frac{\mathrm{2}\pi}{\mathrm{9}\sqrt{\mathrm{3}}}−\frac{\pi^{\mathrm{2}} }{\mathrm{81}}−\frac{\pi{ln}\left(\mathrm{3}\right)}{\mathrm{9}\sqrt{\mathrm{3}}} \\ $$$$ \\ $$
