given-that-1-2pi-e-t-2-2-2-dt-1-and-g-n-u-1-2pi-x-u-n-e-t-2-2-2-dt-and-f-n-u-1-2pi-t-u-n-e-t-

Question Number 697 by 123456 last updated on 02/Mar/15

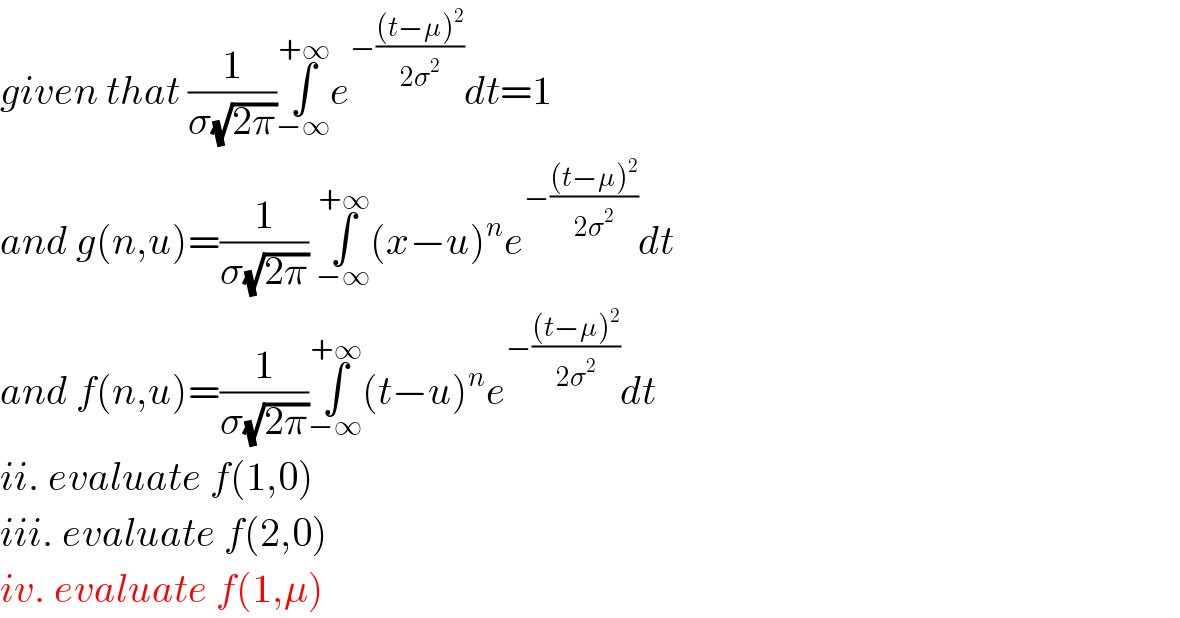
$${given}\:{that}\:\frac{\mathrm{1}}{\sigma\sqrt{\mathrm{2}\pi}}\underset{−\infty} {\overset{+\infty} {\int}}{e}^{−\frac{\left({t}−\mu\right)^{\mathrm{2}} }{\mathrm{2}\sigma^{\mathrm{2}} }} {dt}=\mathrm{1} \\ $$$${and}\:{g}\left({n},{u}\right)=\frac{\mathrm{1}}{\sigma\sqrt{\mathrm{2}\pi}}\:\underset{−\infty} {\overset{+\infty} {\int}}\left({x}−{u}\right)^{{n}} {e}^{−\frac{\left({t}−\mu\right)^{\mathrm{2}} }{\mathrm{2}\sigma^{\mathrm{2}} }} {dt} \\ $$$${and}\:{f}\left({n},{u}\right)=\frac{\mathrm{1}}{\sigma\sqrt{\mathrm{2}\pi}}\underset{−\infty} {\overset{+\infty} {\int}}\left({t}−{u}\right)^{{n}} {e}^{−\frac{\left({t}−\mu\right)^{\mathrm{2}} }{\mathrm{2}\sigma^{\mathrm{2}} }} {dt} \\ $$$${ii}.\:{evaluate}\:{f}\left(\mathrm{1},\mathrm{0}\right) \\ $$$${iii}.\:{evaluate}\:{f}\left(\mathrm{2},\mathrm{0}\right) \\ $$$${iv}.\:{evaluate}\:{f}\left(\mathrm{1},\mu\right) \\ $$

Commented by prakash jain last updated on 01/Mar/15

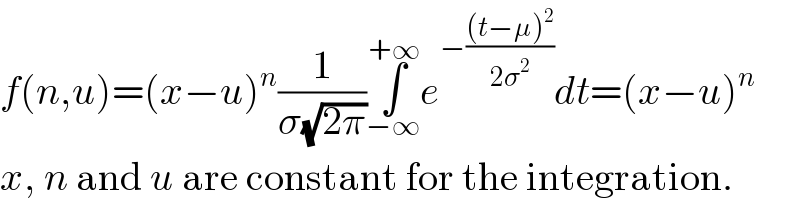
$${f}\left({n},{u}\right)=\left({x}−{u}\right)^{{n}} \frac{\mathrm{1}}{\sigma\sqrt{\mathrm{2}\pi}}\underset{−\infty} {\overset{+\infty} {\int}}{e}^{−\frac{\left({t}−\mu\right)^{\mathrm{2}} }{\mathrm{2}\sigma^{\mathrm{2}} }} {dt}=\left({x}−{u}\right)^{{n}} \\ $$$${x},\:{n}\:\mathrm{and}\:{u}\:\mathrm{are}\:\mathrm{constant}\:\mathrm{for}\:\mathrm{the}\:\mathrm{integration}. \\ $$

Answered by prakash jain last updated on 01/Mar/15

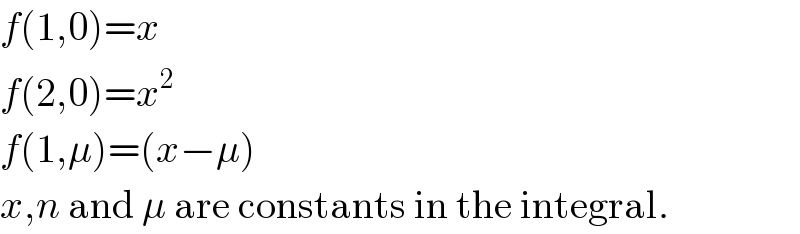
$${f}\left(\mathrm{1},\mathrm{0}\right)={x} \\ $$$${f}\left(\mathrm{2},\mathrm{0}\right)={x}^{\mathrm{2}} \\ $$$${f}\left(\mathrm{1},\mu\right)=\left({x}−\mu\right) \\ $$$${x},{n}\:\mathrm{and}\:\mu\:\mathrm{are}\:\mathrm{constants}\:\mathrm{in}\:\mathrm{the}\:\mathrm{integral}. \\ $$

Terms of Service
Privacy Policy
Contact: info@tinkutara.com