Question Number 68712 by Rio Michael last updated on 15/Sep/19
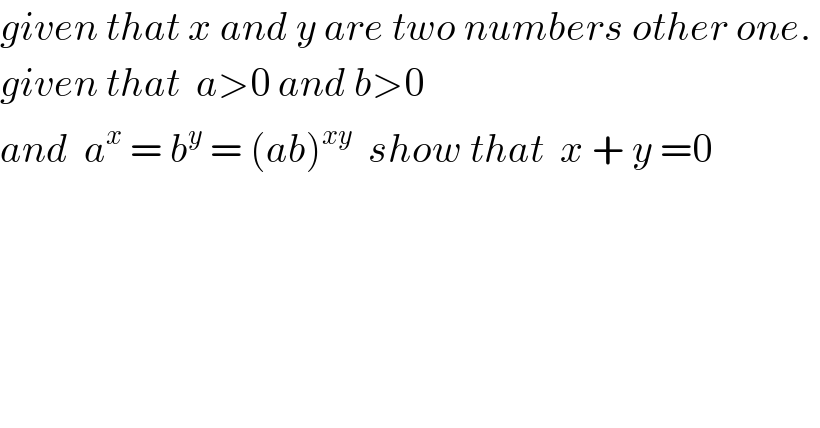
$${given}\:{that}\:{x}\:{and}\:{y}\:{are}\:{two}\:{numbers}\:{other}\:{one}.\: \\ $$$${given}\:{that}\:\:{a}>\mathrm{0}\:{and}\:{b}>\mathrm{0} \\ $$$${and}\:\:{a}^{{x}} \:=\:{b}^{{y}} \:=\:\left({ab}\right)^{{xy}} \:\:{show}\:{that}\:\:{x}\:+\:{y}\:=\mathrm{0} \\ $$
Commented by Prithwish sen last updated on 15/Sep/19

$$\mathrm{Let}\:\mathrm{a}^{\mathrm{x}} =\mathrm{b}^{\mathrm{y}} =\left(\mathrm{ab}\right)^{\mathrm{xy}} =\boldsymbol{\mathrm{k}} \\ $$$$\therefore\:\boldsymbol{\mathrm{a}}=\boldsymbol{\mathrm{k}}^{\frac{\mathrm{1}}{\boldsymbol{\mathrm{x}}}} \\ $$$$\boldsymbol{\mathrm{b}}=\boldsymbol{\mathrm{k}}^{\frac{\mathrm{1}}{\boldsymbol{\mathrm{y}}}} \\ $$$$\boldsymbol{\mathrm{ab}}=\boldsymbol{\mathrm{k}}^{\frac{\mathrm{1}}{\boldsymbol{\mathrm{xy}}}} \\ $$$$\therefore\mathrm{k}^{\frac{\mathrm{1}}{\mathrm{x}}} .\mathrm{k}^{\frac{\mathrm{1}}{\mathrm{y}}} =\mathrm{k}^{\frac{\mathrm{1}}{\mathrm{xy}}} \Rightarrow\frac{\mathrm{1}}{\boldsymbol{\mathrm{x}}}+\frac{\mathrm{1}}{\boldsymbol{\mathrm{y}}}\:=\:\frac{\mathrm{1}}{\boldsymbol{\mathrm{xy}}}\Rightarrow\boldsymbol{\mathrm{x}}+\boldsymbol{\mathrm{y}}=\mathrm{1} \\ $$$$\boldsymbol{\mathrm{please}}\:\boldsymbol{\mathrm{check}} \\ $$
Commented by MJS last updated on 15/Sep/19
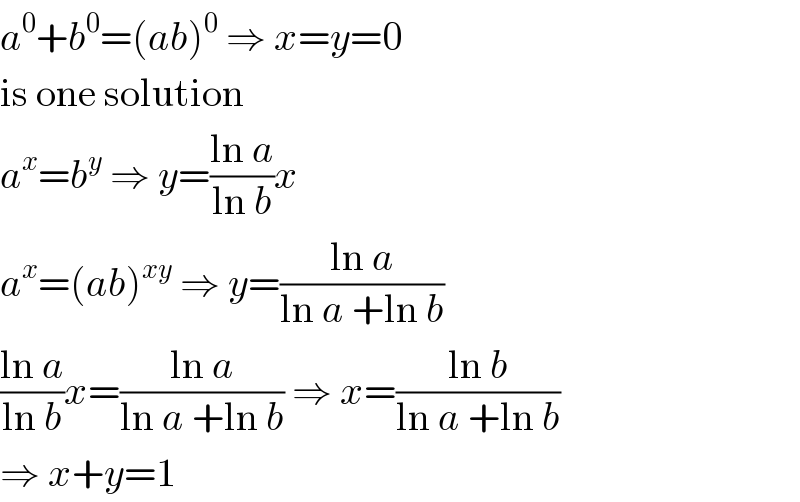
$${a}^{\mathrm{0}} +{b}^{\mathrm{0}} =\left({ab}\right)^{\mathrm{0}} \:\Rightarrow\:{x}={y}=\mathrm{0} \\ $$$$\mathrm{is}\:\mathrm{one}\:\mathrm{solution} \\ $$$${a}^{{x}} ={b}^{{y}} \:\Rightarrow\:{y}=\frac{\mathrm{ln}\:{a}}{\mathrm{ln}\:{b}}{x} \\ $$$${a}^{{x}} =\left({ab}\right)^{{xy}} \:\Rightarrow\:{y}=\frac{\mathrm{ln}\:{a}}{\mathrm{ln}\:{a}\:+\mathrm{ln}\:{b}} \\ $$$$\frac{\mathrm{ln}\:{a}}{\mathrm{ln}\:{b}}{x}=\frac{\mathrm{ln}\:{a}}{\mathrm{ln}\:{a}\:+\mathrm{ln}\:{b}}\:\Rightarrow\:{x}=\frac{\mathrm{ln}\:{b}}{\mathrm{ln}\:{a}\:+\mathrm{ln}\:{b}} \\ $$$$\Rightarrow\:{x}+{y}=\mathrm{1} \\ $$
Commented by Prithwish sen last updated on 15/Sep/19

$$\mathrm{Thanks}\:\mathrm{Sir}. \\ $$
