Menu Close

Given-vector-a-i-2j-k-b-2i-j-2k-c-i-3j-k-and-d-2j-2k-Find-the-value-of-a-b-c-d-

Tinku Tara 0 Comments
Pin




Question Number 133925 by bemath last updated on 25/Feb/21
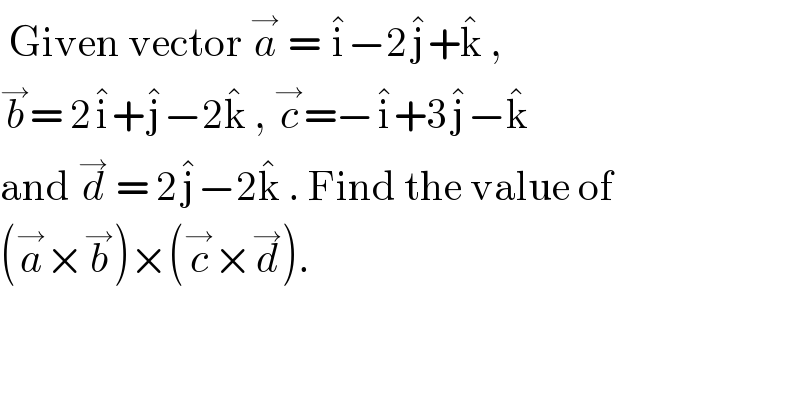
Given vector a^→ = i^� −2j^� +k^� , b^→ = 2i^� +j^� −2k^� , c^→ =−i^� +3j^� −k^� and d^→ = 2j^� −2k^� . Find the value of (a^→ ×b^→ )×(c^→ ×d^→ ).
$$\:\mathrm{Given}\:\mathrm{vector}\:\overset{\rightarrow} {{a}}\:=\:\hat {\mathrm{i}}−\mathrm{2}\hat {\mathrm{j}}+\hat {\mathrm{k}}\:,\: \\ $$$$\overset{\rightarrow} {{b}}=\:\mathrm{2}\hat {\mathrm{i}}+\hat {\mathrm{j}}−\mathrm{2}\hat {\mathrm{k}}\:,\:\overset{\rightarrow} {{c}}=−\hat {\mathrm{i}}+\mathrm{3}\hat {\mathrm{j}}−\hat {\mathrm{k}} \\ $$$$\mathrm{and}\:\overset{\rightarrow} {{d}}\:=\:\mathrm{2}\hat {\mathrm{j}}−\mathrm{2}\hat {\mathrm{k}}\:.\:\mathrm{Find}\:\mathrm{the}\:\mathrm{value}\:\mathrm{of} \\ $$$$\left(\overset{\rightarrow} {{a}}×\overset{\rightarrow} {{b}}\right)×\left(\overset{\rightarrow} {{c}}×\overset{\rightarrow} {{d}}\right). \\ $$
Answered by EDWIN88 last updated on 25/Feb/21
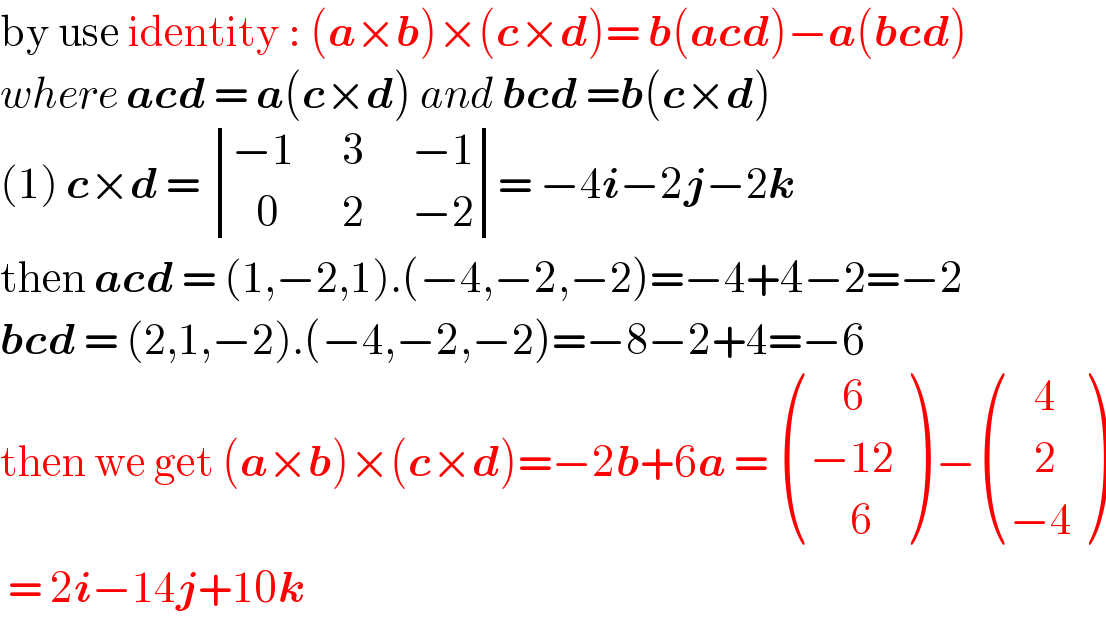
by use identity : (a×b)×(c×d)= b(acd)−a(bcd) where acd = a(c×d) and bcd =b(c×d) (1) c×d = determinant (((−1 3 −1)),(( 0 2 −2)))= −4i−2j−2k then acd = (1,−2,1).(−4,−2,−2)=−4+4−2=−2 bcd = (2,1,−2).(−4,−2,−2)=−8−2+4=−6 then we get (a×b)×(c×d)=−2b+6a = ((( 6)),((−12)),(( 6)) ) − ((( 4)),(( 2)),((−4)) ) = 2i−14j+10k
$$\mathrm{by}\:\mathrm{use}\:\mathrm{identity}\::\:\left(\boldsymbol{{a}}×\boldsymbol{{b}}\right)×\left(\boldsymbol{{c}}×\boldsymbol{{d}}\right)=\:\boldsymbol{{b}}\left(\boldsymbol{{acd}}\right)−\boldsymbol{{a}}\left(\boldsymbol{{bcd}}\right) \\ $$$${where}\:\boldsymbol{{acd}}\:=\:\boldsymbol{{a}}\left(\boldsymbol{{c}}×\boldsymbol{{d}}\right)\:{and}\:\boldsymbol{{bcd}}\:=\boldsymbol{{b}}\left(\boldsymbol{{c}}×\boldsymbol{{d}}\right)\: \\ $$$$\left(\mathrm{1}\right)\:\boldsymbol{{c}}×\boldsymbol{{d}}\:=\:\begin{vmatrix}{−\mathrm{1}\:\:\:\:\:\:\mathrm{3}\:\:\:\:\:\:−\mathrm{1}}\\{\:\:\:\mathrm{0}\:\:\:\:\:\:\:\:\mathrm{2}\:\:\:\:\:\:−\mathrm{2}}\end{vmatrix}=\:−\mathrm{4}\boldsymbol{{i}}−\mathrm{2}\boldsymbol{{j}}−\mathrm{2}\boldsymbol{{k}} \\ $$$$\mathrm{then}\:\boldsymbol{{acd}}\:=\:\left(\mathrm{1},−\mathrm{2},\mathrm{1}\right).\left(−\mathrm{4},−\mathrm{2},−\mathrm{2}\right)=−\mathrm{4}+\mathrm{4}−\mathrm{2}=−\mathrm{2} \\ $$$$\boldsymbol{{bcd}}\:=\:\left(\mathrm{2},\mathrm{1},−\mathrm{2}\right).\left(−\mathrm{4},−\mathrm{2},−\mathrm{2}\right)=−\mathrm{8}−\mathrm{2}+\mathrm{4}=−\mathrm{6} \\ $$$$\mathrm{then}\:\mathrm{we}\:\mathrm{get}\:\left(\boldsymbol{{a}}×\boldsymbol{{b}}\right)×\left(\boldsymbol{{c}}×\boldsymbol{{d}}\right)=−\mathrm{2}\boldsymbol{{b}}+\mathrm{6}\boldsymbol{{a}}\:=\:\begin{pmatrix}{\:\:\:\:\mathrm{6}}\\{−\mathrm{12}}\\{\:\:\:\:\:\mathrm{6}}\end{pmatrix}\:−\begin{pmatrix}{\:\:\:\mathrm{4}}\\{\:\:\:\mathrm{2}}\\{−\mathrm{4}}\end{pmatrix} \\ $$$$\:=\:\mathrm{2}\boldsymbol{{i}}−\mathrm{14}\boldsymbol{{j}}+\mathrm{10}\boldsymbol{{k}}\: \\ $$
Answered by bemath last updated on 25/Feb/21
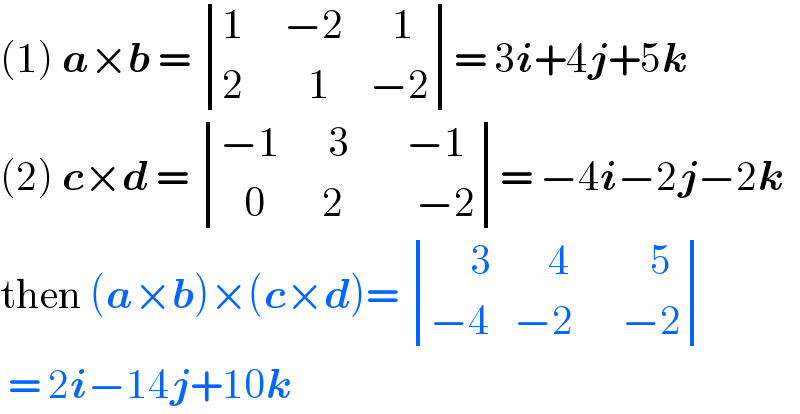
(1) a×b = determinant (((1 −2 1)),((2 1 −2)))= 3i+4j+5k (2) c×d = determinant (((−1 3 −1)),(( 0 2 −2)))= −4i−2j−2k then (a×b)×(c×d)= determinant ((( 3 4 5)),((−4 −2 −2))) = 2i−14j+10k
$$\left(\mathrm{1}\right)\:\boldsymbol{{a}}×\boldsymbol{{b}}\:=\:\begin{vmatrix}{\mathrm{1}\:\:\:\:\:−\mathrm{2}\:\:\:\:\:\:\mathrm{1}}\\{\mathrm{2}\:\:\:\:\:\:\:\:\mathrm{1}\:\:\:\:\:−\mathrm{2}}\end{vmatrix}=\:\mathrm{3}\boldsymbol{{i}}+\mathrm{4}\boldsymbol{{j}}+\mathrm{5}\boldsymbol{{k}} \\ $$$$\left(\mathrm{2}\right)\:\boldsymbol{{c}}×\boldsymbol{{d}}\:=\:\begin{vmatrix}{−\mathrm{1}\:\:\:\:\:\:\mathrm{3}\:\:\:\:\:\:\:−\mathrm{1}}\\{\:\:\:\mathrm{0}\:\:\:\:\:\:\:\mathrm{2}\:\:\:\:\:\:\:\:\:−\mathrm{2}}\end{vmatrix}=\:−\mathrm{4}\boldsymbol{{i}}−\mathrm{2}\boldsymbol{{j}}−\mathrm{2}\boldsymbol{{k}} \\ $$$$\mathrm{then}\:\left(\boldsymbol{{a}}×\boldsymbol{{b}}\right)×\left(\boldsymbol{{c}}×\boldsymbol{{d}}\right)=\:\begin{vmatrix}{\:\:\:\:\:\mathrm{3}\:\:\:\:\:\:\:\mathrm{4}\:\:\:\:\:\:\:\:\:\:\mathrm{5}}\\{−\mathrm{4}\:\:\:−\mathrm{2}\:\:\:\:\:\:−\mathrm{2}}\end{vmatrix} \\ $$$$\:=\:\mathrm{2}\boldsymbol{{i}}−\mathrm{14}\boldsymbol{{j}}+\mathrm{10}\boldsymbol{{k}} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *