Question Number 66084 by F_Nongue last updated on 09/Aug/19
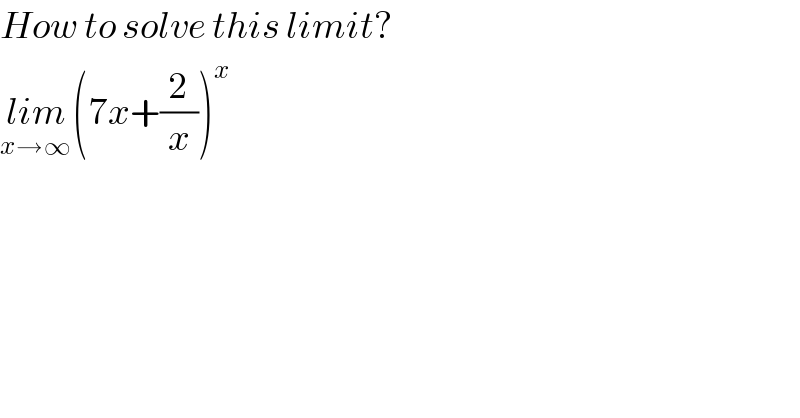
$${How}\:{to}\:{solve}\:{this}\:{limit}? \\ $$$$\underset{{x}\rightarrow\infty} {{lim}}\left(\mathrm{7}{x}+\frac{\mathrm{2}}{{x}}\right)^{{x}} \\ $$
Commented by mathmax by abdo last updated on 09/Aug/19
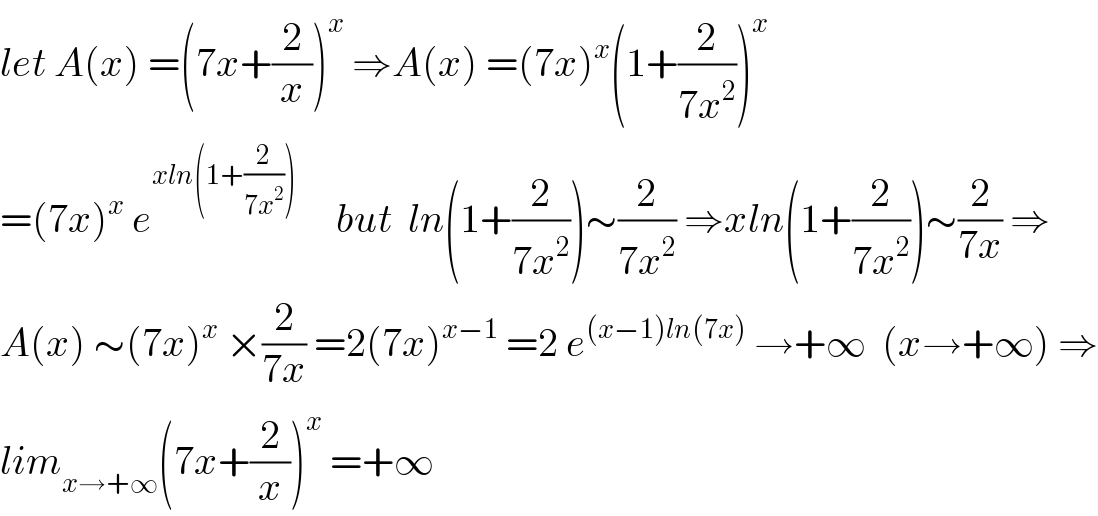
$${let}\:{A}\left({x}\right)\:=\left(\mathrm{7}{x}+\frac{\mathrm{2}}{{x}}\right)^{{x}} \:\Rightarrow{A}\left({x}\right)\:=\left(\mathrm{7}{x}\right)^{{x}} \left(\mathrm{1}+\frac{\mathrm{2}}{\mathrm{7}{x}^{\mathrm{2}} }\right)^{{x}} \\ $$$$=\left(\mathrm{7}{x}\right)^{{x}} \:{e}^{{xln}\left(\mathrm{1}+\frac{\mathrm{2}}{\mathrm{7}{x}^{\mathrm{2}} }\right)} \:\:\:\:\:{but}\:\:{ln}\left(\mathrm{1}+\frac{\mathrm{2}}{\mathrm{7}{x}^{\mathrm{2}} }\right)\sim\frac{\mathrm{2}}{\mathrm{7}{x}^{\mathrm{2}} }\:\Rightarrow{xln}\left(\mathrm{1}+\frac{\mathrm{2}}{\mathrm{7}{x}^{\mathrm{2}} }\right)\sim\frac{\mathrm{2}}{\mathrm{7}{x}}\:\Rightarrow \\ $$$${A}\left({x}\right)\:\sim\left(\mathrm{7}{x}\right)^{{x}} \:×\frac{\mathrm{2}}{\mathrm{7}{x}}\:=\mathrm{2}\left(\mathrm{7}{x}\right)^{{x}−\mathrm{1}} \:=\mathrm{2}\:{e}^{\left({x}−\mathrm{1}\right){ln}\left(\mathrm{7}{x}\right)} \:\rightarrow+\infty\:\:\left({x}\rightarrow+\infty\right)\:\Rightarrow \\ $$$${lim}_{{x}\rightarrow+\infty} \left(\mathrm{7}{x}+\frac{\mathrm{2}}{{x}}\right)^{{x}} \:=+\infty\: \\ $$
Answered by MJS last updated on 09/Aug/19

$$\left(\mathrm{7}{x}+\frac{\mathrm{2}}{{x}}\right)^{{x}} =\left(\frac{\mathrm{7}{x}^{\mathrm{2}} +\mathrm{2}}{{x}}\right)^{{x}} =\frac{\left(\mathrm{7}{x}^{\mathrm{2}} +\mathrm{2}\right)^{{x}} }{{x}^{{x}} } \\ $$$$\underset{{x}\rightarrow\infty} {\mathrm{lim}}\frac{\left(\mathrm{7}{x}^{\mathrm{2}} +\mathrm{2}\right)^{{x}} }{{x}^{{x}} }>\underset{{x}\rightarrow\infty} {\mathrm{lim}}\frac{\left(\mathrm{7}{x}^{\mathrm{2}} \right)^{{x}} }{{x}^{{x}} }=\underset{{x}\rightarrow\infty} {\mathrm{lim}7}^{{x}} {x}^{{x}} =+\infty \\ $$
Commented by Prithwish sen last updated on 09/Aug/19

$$\:\frac{\mathrm{2}}{\mathrm{x}}\rightarrow\mathrm{0}\:\mathrm{as}\:\mathrm{x}\rightarrow\infty\:\therefore\:\left(\mathrm{7x}+\frac{\mathrm{2}}{\mathrm{x}}\right)^{\mathrm{x}} \rightarrow\mathrm{7}^{\mathrm{x}} \mathrm{x}^{\mathrm{x}} \\ $$
