Menu Close

If-and-are-roots-of-the-equation-x-3-px-q-0-p-0-q-0-then-find-the-value-of-the-determinant-determinant-

Tinku Tara
Pin




Question Number 363 by rajabhay last updated on 25/Jan/15
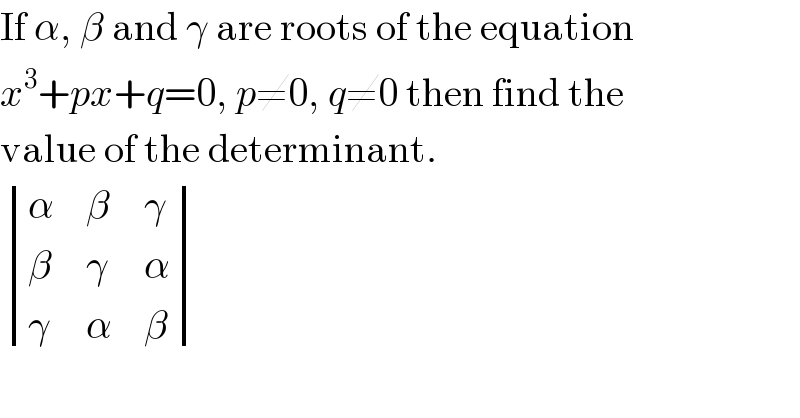
If α, β and γ are roots of the equation x^3 +px+q=0, p≠0, q≠0 then find the value of the determinant. determinant ((α,β,γ),(β,γ,α),(γ,α,β))
$$\mathrm{If}\:\alpha,\:\beta\:\mathrm{and}\:\gamma\:\mathrm{are}\:\mathrm{roots}\:\mathrm{of}\:\mathrm{the}\:\mathrm{equation} \\ $$$${x}^{\mathrm{3}} +{px}+{q}=\mathrm{0},\:{p}\neq\mathrm{0},\:{q}\neq\mathrm{0}\:\mathrm{then}\:\mathrm{find}\:\mathrm{the} \\ $$$$\mathrm{value}\:\mathrm{of}\:\mathrm{the}\:\mathrm{determinant}. \\ $$$$\begin{vmatrix}{\alpha}&{\beta}&{\gamma}\\{\beta}&{\gamma}&{\alpha}\\{\gamma}&{\alpha}&{\beta}\end{vmatrix} \\ $$
Commented by 123456 last updated on 24/Dec/14
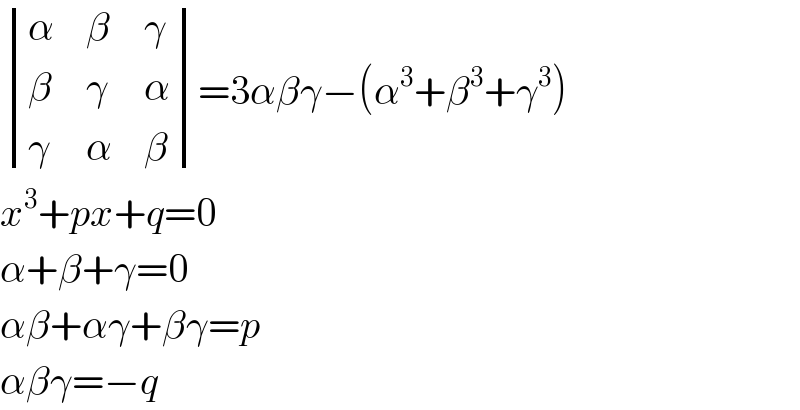
determinant ((α,β,γ),(β,γ,α),(γ,α,β))=3αβγ−(α^3 +β^3 +γ^3 ) x^3 +px+q=0 α+β+γ=0 αβ+αγ+βγ=p αβγ=−q
$$\begin{vmatrix}{\alpha}&{\beta}&{\gamma}\\{\beta}&{\gamma}&{\alpha}\\{\gamma}&{\alpha}&{\beta}\end{vmatrix}=\mathrm{3}\alpha\beta\gamma−\left(\alpha^{\mathrm{3}} +\beta^{\mathrm{3}} +\gamma^{\mathrm{3}} \right) \\ $$$${x}^{\mathrm{3}} +{px}+{q}=\mathrm{0} \\ $$$$\alpha+\beta+\gamma=\mathrm{0} \\ $$$$\alpha\beta+\alpha\gamma+\beta\gamma={p} \\ $$$$\alpha\beta\gamma=−{q} \\ $$
Answered by prakash jain last updated on 24/Dec/14
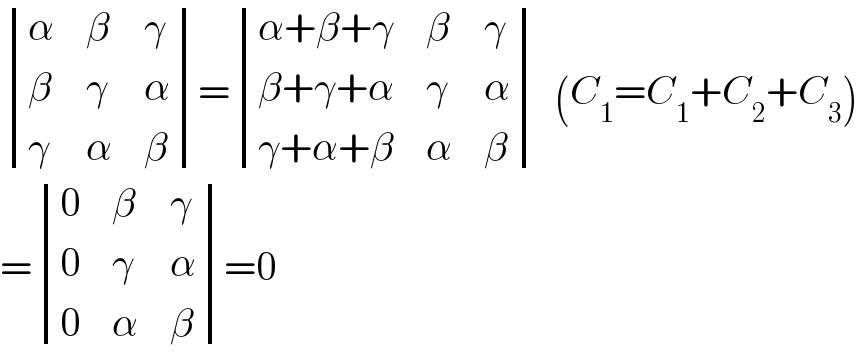
determinant ((α,β,γ),(β,γ,α),(γ,α,β))= determinant (((α+β+γ),β,γ),((β+γ+α),γ,α),((γ+α+β),α,β)) (C_1 =C_1 +C_2 +C_3 ) = determinant ((0,β,γ),(0,γ,α),(0,α,β))=0
$$\begin{vmatrix}{\alpha}&{\beta}&{\gamma}\\{\beta}&{\gamma}&{\alpha}\\{\gamma}&{\alpha}&{\beta}\end{vmatrix}=\begin{vmatrix}{\alpha+\beta+\gamma}&{\beta}&{\gamma}\\{\beta+\gamma+\alpha}&{\gamma}&{\alpha}\\{\gamma+\alpha+\beta}&{\alpha}&{\beta}\end{vmatrix}\:\:\left({C}_{\mathrm{1}} ={C}_{\mathrm{1}} +{C}_{\mathrm{2}} +{C}_{\mathrm{3}} \right) \\ $$$$=\begin{vmatrix}{\mathrm{0}}&{\beta}&{\gamma}\\{\mathrm{0}}&{\gamma}&{\alpha}\\{\mathrm{0}}&{\alpha}&{\beta}\end{vmatrix}=\mathrm{0} \\ $$

Pin