Question Number 131296 by EDWIN88 last updated on 03/Feb/21
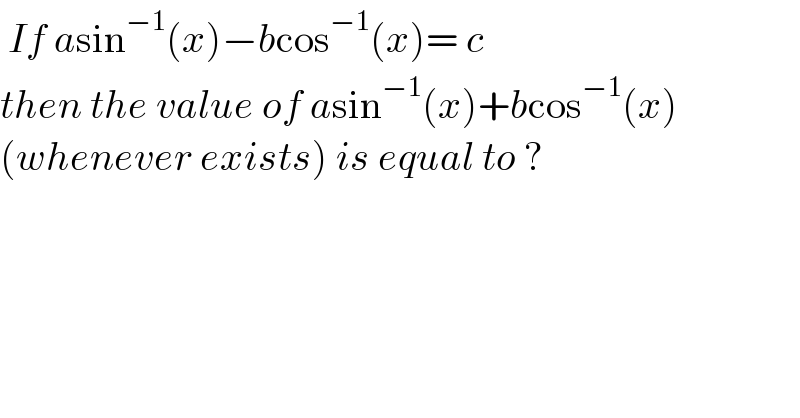
$$\:{If}\:{a}\mathrm{sin}^{−\mathrm{1}} \left({x}\right)−{b}\mathrm{cos}^{−\mathrm{1}} \left({x}\right)=\:{c}\: \\ $$$${then}\:{the}\:{value}\:{of}\:{a}\mathrm{sin}^{−\mathrm{1}} \left({x}\right)+{b}\mathrm{cos}^{−\mathrm{1}} \left({x}\right)\: \\ $$$$\left({whenever}\:{exists}\right)\:{is}\:{equal}\:{to}\:? \\ $$
Answered by liberty last updated on 03/Feb/21
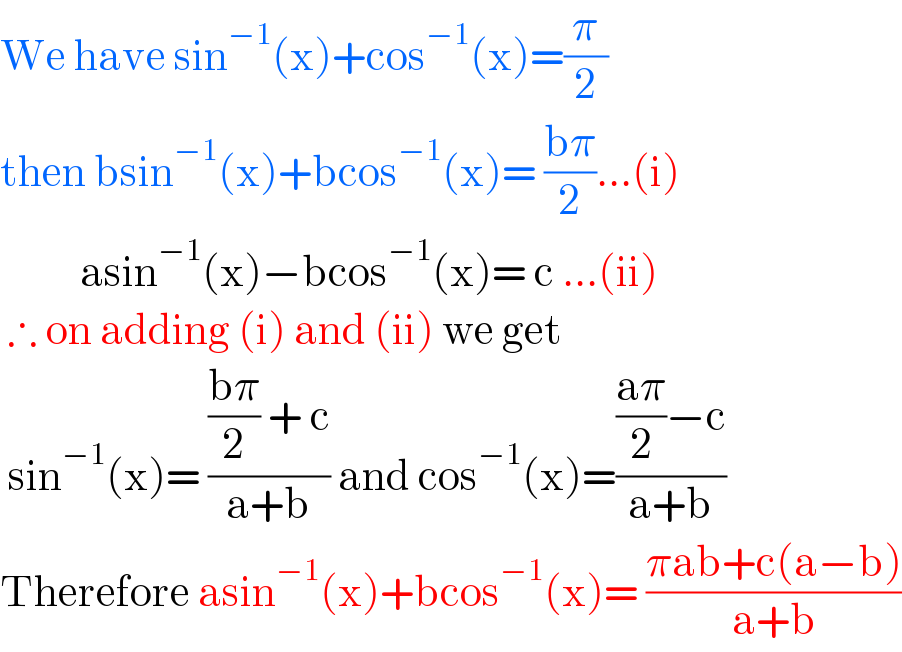
$$\mathrm{We}\:\mathrm{have}\:\mathrm{sin}^{−\mathrm{1}} \left(\mathrm{x}\right)+\mathrm{cos}^{−\mathrm{1}} \left(\mathrm{x}\right)=\frac{\pi}{\mathrm{2}} \\ $$$$\mathrm{then}\:\mathrm{bsin}^{−\mathrm{1}} \left(\mathrm{x}\right)+\mathrm{bcos}^{−\mathrm{1}} \left(\mathrm{x}\right)=\:\frac{\mathrm{b}\pi}{\mathrm{2}}…\left(\mathrm{i}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\mathrm{asin}^{−\mathrm{1}} \left(\mathrm{x}\right)−\mathrm{bcos}^{−\mathrm{1}} \left(\mathrm{x}\right)=\:\mathrm{c}\:…\left(\mathrm{ii}\right) \\ $$$$\:\therefore\:\mathrm{on}\:\mathrm{adding}\:\left(\mathrm{i}\right)\:\mathrm{and}\:\left(\mathrm{ii}\right)\:\mathrm{we}\:\mathrm{get}\: \\ $$$$\:\mathrm{sin}^{−\mathrm{1}} \left(\mathrm{x}\right)=\:\frac{\frac{\mathrm{b}\pi}{\mathrm{2}}\:+\:\mathrm{c}}{\mathrm{a}+\mathrm{b}}\:\mathrm{and}\:\mathrm{cos}^{−\mathrm{1}} \left(\mathrm{x}\right)=\frac{\frac{\mathrm{a}\pi}{\mathrm{2}}−\mathrm{c}}{\mathrm{a}+\mathrm{b}} \\ $$$$\mathrm{Therefore}\:\mathrm{asin}^{−\mathrm{1}} \left(\mathrm{x}\right)+\mathrm{bcos}^{−\mathrm{1}} \left(\mathrm{x}\right)=\:\frac{\pi\mathrm{ab}+\mathrm{c}\left(\mathrm{a}−\mathrm{b}\right)}{\mathrm{a}+\mathrm{b}} \\ $$
Commented by EDWIN88 last updated on 03/Feb/21

$$ \\ $$$$\mathrm{sehr}\:\mathrm{interessante}\:\mathrm{Erklrung}\:\mathrm{Sir}\: \\ $$
Answered by mr W last updated on 03/Feb/21
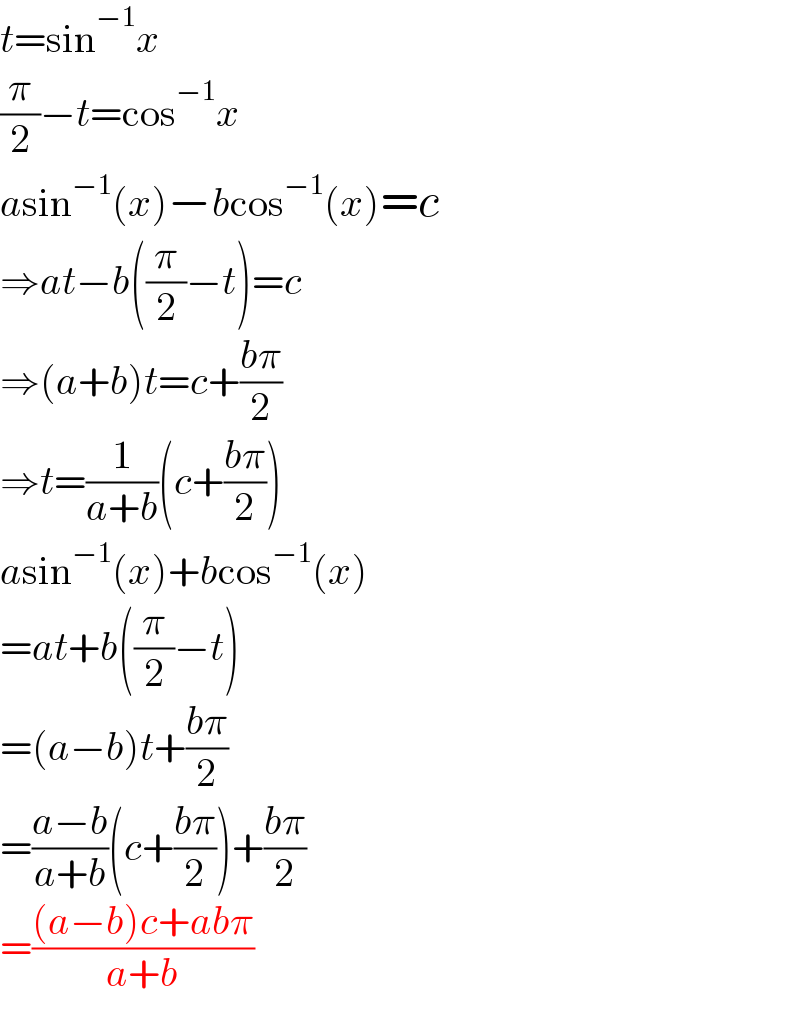
$${t}=\mathrm{sin}^{−\mathrm{1}} {x} \\ $$$$\frac{\pi}{\mathrm{2}}−{t}=\mathrm{cos}^{−\mathrm{1}} {x} \\ $$$${a}\mathrm{sin}^{−\mathrm{1}} \left({x}\right)−{b}\mathrm{cos}^{−\mathrm{1}} \left({x}\right)={c} \\ $$$$\Rightarrow{at}−{b}\left(\frac{\pi}{\mathrm{2}}−{t}\right)={c} \\ $$$$\Rightarrow\left({a}+{b}\right){t}={c}+\frac{{b}\pi}{\mathrm{2}} \\ $$$$\Rightarrow{t}=\frac{\mathrm{1}}{{a}+{b}}\left({c}+\frac{{b}\pi}{\mathrm{2}}\right) \\ $$$${a}\mathrm{sin}^{−\mathrm{1}} \left({x}\right)+{b}\mathrm{cos}^{−\mathrm{1}} \left({x}\right)\: \\ $$$$={at}+{b}\left(\frac{\pi}{\mathrm{2}}−{t}\right) \\ $$$$=\left({a}−{b}\right){t}+\frac{{b}\pi}{\mathrm{2}} \\ $$$$=\frac{{a}−{b}}{{a}+{b}}\left({c}+\frac{{b}\pi}{\mathrm{2}}\right)+\frac{{b}\pi}{\mathrm{2}} \\ $$$$=\frac{\left({a}−{b}\right){c}+{ab}\pi}{{a}+{b}} \\ $$
Commented by EDWIN88 last updated on 03/Feb/21

$${nice} \\ $$
