Question Number 11067 by suci last updated on 10/Mar/17

$${if}\:{E}=\left\{{f}\mid{f}:\mathbb{R}\rightarrow\mathbb{R}\:{continuous}\:{function}\:{with}\:{f}\left({x}\right)\in\mathbb{Q},\:\forall{x}\in\mathbb{R}\right\}, \\ $$$${then}\:{E}=….??? \\ $$
Commented by FilupS last updated on 10/Mar/17

$$\mathbb{Q}\:=\:\mathrm{irrational}\:\mathrm{numbers}\:\mathrm{set} \\ $$$$ \\ $$$$\mathrm{one}\:\mathrm{example}\:\left(\mathrm{i}\:\mathrm{think}\right): \\ $$$${f}\left({x}\right)=\frac{\mathrm{2}{x}+\mathrm{1}}{\mathrm{2}{x}} \\ $$$$\mathrm{or} \\ $$$${f}\left({x}\right)=\frac{\mathrm{2}{x}}{\mathrm{2}{x}+\mathrm{1}} \\ $$
Commented by FilupS last updated on 11/Mar/17
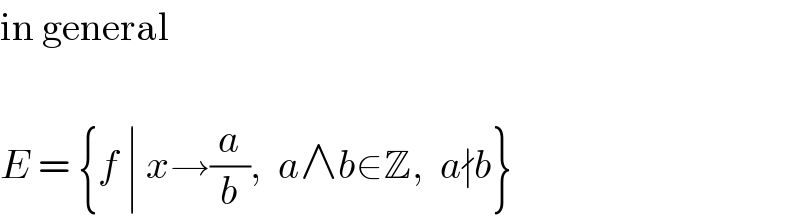
$$\mathrm{in}\:\mathrm{general} \\ $$$$\: \\ $$$${E}\:=\:\left\{{f}\:\mid\:{x}\rightarrow\frac{{a}}{{b}},\:\:{a}\wedge{b}\in\mathbb{Z},\:\:{a}\nmid{b}\right\} \\ $$
Commented by FilupS last updated on 11/Mar/17
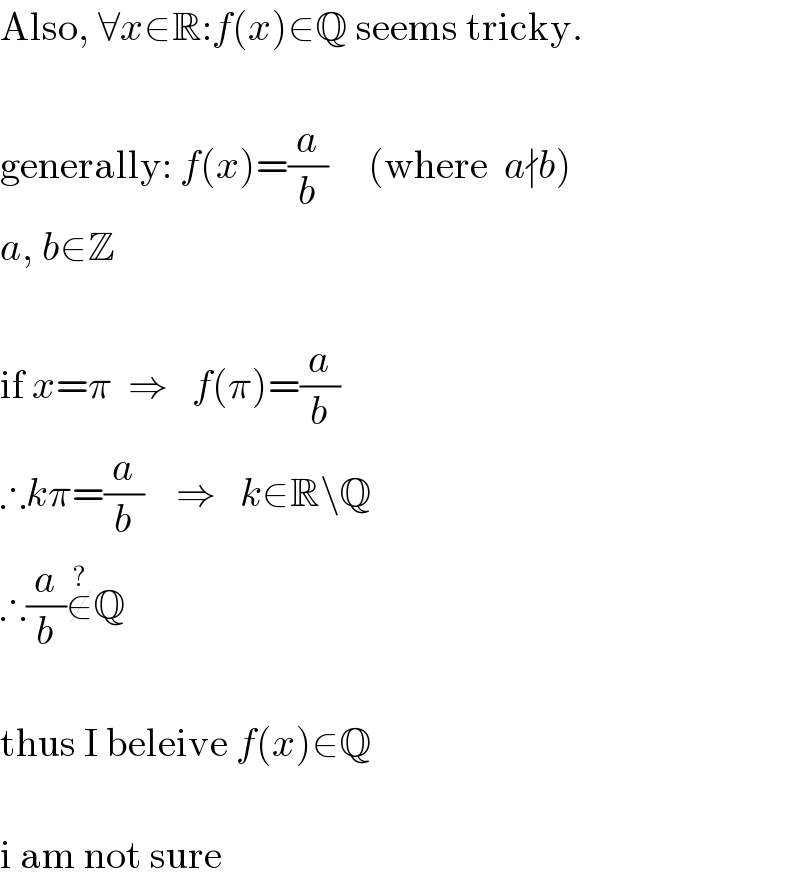
$$\mathrm{Also},\:\forall{x}\in\mathbb{R}:{f}\left({x}\right)\in\mathbb{Q}\:\mathrm{seems}\:\mathrm{tricky}. \\ $$$$\: \\ $$$$\mathrm{generally}:\:{f}\left({x}\right)=\frac{{a}}{{b}}\:\:\:\:\:\left(\mathrm{where}\:\:{a}\nmid{b}\right) \\ $$$${a},\:{b}\in\mathbb{Z} \\ $$$$\: \\ $$$$\mathrm{if}\:{x}=\pi\:\:\Rightarrow\:\:\:{f}\left(\pi\right)=\frac{{a}}{{b}} \\ $$$$\therefore{k}\pi=\frac{{a}}{{b}}\:\:\:\:\Rightarrow\:\:\:{k}\in\mathbb{R}\backslash\mathbb{Q} \\ $$$$\therefore\frac{{a}}{{b}}\overset{?} {\notin}\mathbb{Q} \\ $$$$\: \\ $$$$\mathrm{thus}\:\mathrm{I}\:\mathrm{beleive}\:{f}\left({x}\right)\in\mathbb{Q} \\ $$$$\: \\ $$$$\mathrm{i}\:\mathrm{am}\:\mathrm{not}\:\mathrm{sure} \\ $$
Commented by prakash jain last updated on 12/Mar/17

$$\mathrm{If}\:{f}\left({x}\right)\:\mathrm{is}\:\mathrm{continuous}\:\mathrm{and}\:{f}\left({x}\right)\in\mathbb{Q} \\ $$$$\Rightarrow{f}\left({x}\right)={c}\:{where}\:{c}\:{is}\:{a}\:{constant}\:\in\mathbb{Q} \\ $$$${or}\:{E}\:{is}\:{same}\:{as}\:\mathbb{Q} \\ $$
