Question Number 636 by 123456 last updated on 17/Feb/15
![if f,g are functions of R→R not constant such for all (x,y)∈R^2 { ((f(x+y)=f(x)f(y)−g(x)g(y))),((g(x+y)=f(x)g(y)+g(x)f(y))) :} if f′(0)=0 then proof os disproof that ∀x∈R,[f(x)]^2 +[g(x)]^2 =1](https://www.tinkutara.com/question/Q636.png)
$${if}\:{f},{g}\:{are}\:{functions}\:{of}\:\mathbb{R}\rightarrow\mathbb{R} \\ $$$${not}\:{constant}\:{such}\:{for}\:{all}\:\left({x},{y}\right)\in\mathbb{R}^{\mathrm{2}} \\ $$$$\begin{cases}{{f}\left({x}+{y}\right)={f}\left({x}\right){f}\left({y}\right)−{g}\left({x}\right){g}\left({y}\right)}\\{{g}\left({x}+{y}\right)={f}\left({x}\right){g}\left({y}\right)+{g}\left({x}\right){f}\left({y}\right)}\end{cases} \\ $$$${if}\:{f}'\left(\mathrm{0}\right)=\mathrm{0}\:{then}\:{proof}\:{os}\:{disproof} \\ $$$${that}\:\forall{x}\in\mathbb{R},\left[{f}\left({x}\right)\right]^{\mathrm{2}} +\left[{g}\left({x}\right)\right]^{\mathrm{2}} =\mathrm{1} \\ $$
Commented by prakash jain last updated on 16/Feb/15
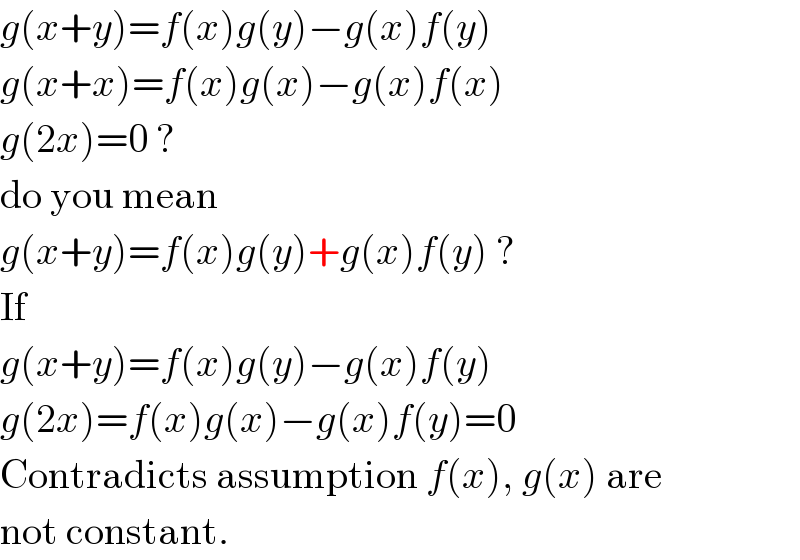
$${g}\left({x}+{y}\right)={f}\left({x}\right){g}\left({y}\right)−{g}\left({x}\right){f}\left({y}\right) \\ $$$${g}\left({x}+{x}\right)={f}\left({x}\right){g}\left({x}\right)−{g}\left({x}\right){f}\left({x}\right) \\ $$$${g}\left(\mathrm{2}{x}\right)=\mathrm{0}\:? \\ $$$$\mathrm{do}\:\mathrm{you}\:\mathrm{mean}\: \\ $$$${g}\left({x}+{y}\right)={f}\left({x}\right){g}\left({y}\right)+{g}\left({x}\right){f}\left({y}\right)\:? \\ $$$$\mathrm{If} \\ $$$${g}\left({x}+{y}\right)={f}\left({x}\right){g}\left({y}\right)−{g}\left({x}\right){f}\left({y}\right) \\ $$$${g}\left(\mathrm{2}{x}\right)={f}\left({x}\right){g}\left({x}\right)−{g}\left({x}\right){f}\left({y}\right)=\mathrm{0} \\ $$$$\mathrm{Contradicts}\:\mathrm{assumption}\:{f}\left({x}\right),\:{g}\left({x}\right)\:\mathrm{are} \\ $$$$\mathrm{not}\:\mathrm{constant}. \\ $$
Commented by prakash jain last updated on 17/Feb/15
![Squaring and adding [f(x+y)]^2 +[g(x+y)]^2 =([f(x)]^2 +[g(x)]^2 )([f(y)]^2 +[g(y)]^2 ) If u(x)=[f(x)]^2 +[g(x)]^2 u(x+y)=u(x)u(y)⇒u(x)=e^(kx) [f(x)]^2 +[g(x)]^2 =e^(kx)](https://www.tinkutara.com/question/Q643.png)
$$\mathrm{Squaring}\:\mathrm{and}\:\mathrm{adding} \\ $$$$\left[{f}\left({x}+{y}\right)\right]^{\mathrm{2}} +\left[{g}\left({x}+{y}\right)\right]^{\mathrm{2}} =\left(\left[{f}\left({x}\right)\right]^{\mathrm{2}} +\left[{g}\left({x}\right)\right]^{\mathrm{2}} \right)\left(\left[{f}\left({y}\right)\right]^{\mathrm{2}} +\left[{g}\left({y}\right)\right]^{\mathrm{2}} \right) \\ $$$$\mathrm{If}\:{u}\left({x}\right)=\left[{f}\left({x}\right)\right]^{\mathrm{2}} +\left[{g}\left({x}\right)\right]^{\mathrm{2}} \\ $$$${u}\left({x}+{y}\right)={u}\left({x}\right){u}\left({y}\right)\Rightarrow{u}\left({x}\right)={e}^{{kx}} \\ $$$$\left[{f}\left({x}\right)\right]^{\mathrm{2}} +\left[{g}\left({x}\right)\right]^{\mathrm{2}} ={e}^{{kx}} \\ $$
Answered by prakash jain last updated on 17/Feb/15
![From comments [f(x)]^2 +[g(x)]^2 =e^(kx) f(x+x)=[f(x)]^2 −[g(x)]^2 f(2x)=2[f(x)]^2 −e^(kx) Differenting both sides 2f ′(2x)=4f(x) f ′(x)−ke^(kx) put x=0 2f ′(0)=4 f(0) f ′(0)−k Given f ′(0)=0 0=0−k⇒k=0 Hence [f(x)]^2 +[g(x)]^2 =1](https://www.tinkutara.com/question/Q644.png)
$$\mathrm{From}\:\mathrm{comments} \\ $$$$\left[{f}\left({x}\right)\right]^{\mathrm{2}} +\left[{g}\left({x}\right)\right]^{\mathrm{2}} ={e}^{{kx}} \\ $$$${f}\left({x}+{x}\right)=\left[{f}\left({x}\right)\right]^{\mathrm{2}} −\left[{g}\left({x}\right)\right]^{\mathrm{2}} \\ $$$${f}\left(\mathrm{2}{x}\right)=\mathrm{2}\left[{f}\left({x}\right)\right]^{\mathrm{2}} −{e}^{{kx}} \\ $$$$\mathrm{Differenting}\:\mathrm{both}\:\mathrm{sides} \\ $$$$\mathrm{2}{f}\:'\left(\mathrm{2}{x}\right)=\mathrm{4}{f}\left({x}\right)\:{f}\:'\left({x}\right)−{ke}^{{kx}} \\ $$$$\mathrm{put}\:{x}=\mathrm{0} \\ $$$$\mathrm{2}{f}\:'\left(\mathrm{0}\right)=\mathrm{4}\:{f}\left(\mathrm{0}\right)\:{f}\:'\left(\mathrm{0}\right)−{k} \\ $$$$\mathrm{Given}\:{f}\:'\left(\mathrm{0}\right)=\mathrm{0} \\ $$$$\mathrm{0}=\mathrm{0}−{k}\Rightarrow{k}=\mathrm{0} \\ $$$$\mathrm{Hence} \\ $$$$\left[{f}\left({x}\right)\right]^{\mathrm{2}} +\left[{g}\left({x}\right)\right]^{\mathrm{2}} =\mathrm{1}\: \\ $$$$ \\ $$
