Menu Close

If-f-x-is-a-function-satisfying-f-x-y-f-x-f-y-for-all-x-y-N-such-that-f-1-3-and-x-1-n-f-x-120-Then-find-the-value-of-n-

Tinku Tara
Pin




Question Number 257 by abcd last updated on 25/Jan/15
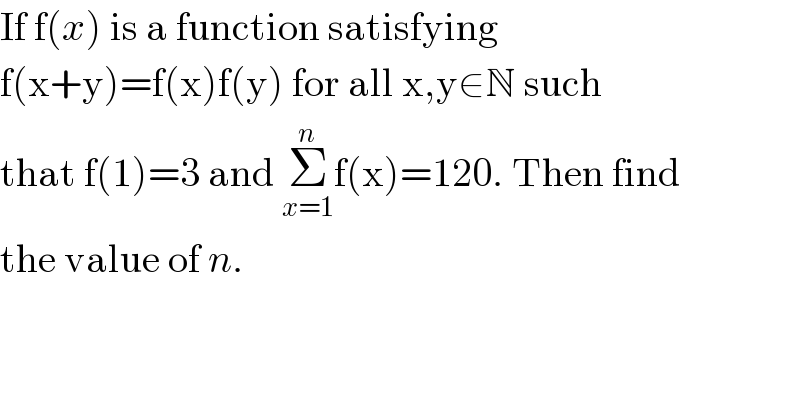
If f(x) is a function satisfying f(x+y)=f(x)f(y) for all x,y∈N such that f(1)=3 and Σ_(x=1) ^n f(x)=120. Then find the value of n.
$$\mathrm{If}\:\mathrm{f}\left({x}\right)\:\mathrm{is}\:\mathrm{a}\:\mathrm{function}\:\mathrm{satisfying} \\ $$$$\mathrm{f}\left(\mathrm{x}+\mathrm{y}\right)=\mathrm{f}\left(\mathrm{x}\right)\mathrm{f}\left(\mathrm{y}\right)\:\mathrm{for}\:\mathrm{all}\:\mathrm{x},\mathrm{y}\in\mathbb{N}\:\mathrm{such} \\ $$$$\mathrm{that}\:\mathrm{f}\left(\mathrm{1}\right)=\mathrm{3}\:\mathrm{and}\:\underset{{x}=\mathrm{1}} {\overset{{n}} {\sum}}\mathrm{f}\left(\mathrm{x}\right)=\mathrm{120}.\:\mathrm{Then}\:\mathrm{find} \\ $$$$\mathrm{the}\:\mathrm{value}\:\mathrm{of}\:{n}. \\ $$
Answered by 123456 last updated on 17/Dec/14
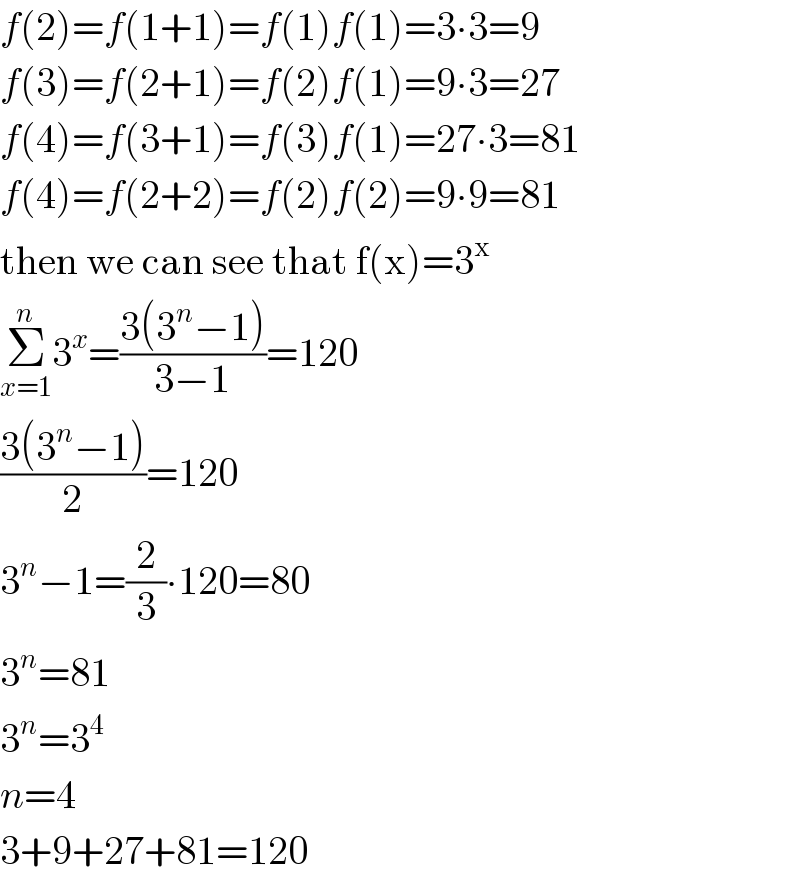
f(2)=f(1+1)=f(1)f(1)=3∙3=9 f(3)=f(2+1)=f(2)f(1)=9∙3=27 f(4)=f(3+1)=f(3)f(1)=27∙3=81 f(4)=f(2+2)=f(2)f(2)=9∙9=81 then we can see that f(x)=3^x Σ_(x=1) ^n 3^x =((3(3^n −1))/(3−1))=120 ((3(3^n −1))/2)=120 3^n −1=(2/3)∙120=80 3^n =81 3^n =3^4 n=4 3+9+27+81=120
$${f}\left(\mathrm{2}\right)={f}\left(\mathrm{1}+\mathrm{1}\right)={f}\left(\mathrm{1}\right){f}\left(\mathrm{1}\right)=\mathrm{3}\centerdot\mathrm{3}=\mathrm{9} \\ $$$${f}\left(\mathrm{3}\right)={f}\left(\mathrm{2}+\mathrm{1}\right)={f}\left(\mathrm{2}\right){f}\left(\mathrm{1}\right)=\mathrm{9}\centerdot\mathrm{3}=\mathrm{27} \\ $$$${f}\left(\mathrm{4}\right)={f}\left(\mathrm{3}+\mathrm{1}\right)={f}\left(\mathrm{3}\right){f}\left(\mathrm{1}\right)=\mathrm{27}\centerdot\mathrm{3}=\mathrm{81} \\ $$$${f}\left(\mathrm{4}\right)={f}\left(\mathrm{2}+\mathrm{2}\right)={f}\left(\mathrm{2}\right){f}\left(\mathrm{2}\right)=\mathrm{9}\centerdot\mathrm{9}=\mathrm{81} \\ $$$$\mathrm{then}\:\mathrm{we}\:\mathrm{can}\:\mathrm{see}\:\mathrm{that}\:\mathrm{f}\left(\mathrm{x}\right)=\mathrm{3}^{\mathrm{x}} \\ $$$$\underset{{x}=\mathrm{1}} {\overset{{n}} {\sum}}\mathrm{3}^{{x}} =\frac{\mathrm{3}\left(\mathrm{3}^{{n}} −\mathrm{1}\right)}{\mathrm{3}−\mathrm{1}}=\mathrm{120} \\ $$$$\frac{\mathrm{3}\left(\mathrm{3}^{{n}} −\mathrm{1}\right)}{\mathrm{2}}=\mathrm{120} \\ $$$$\mathrm{3}^{{n}} −\mathrm{1}=\frac{\mathrm{2}}{\mathrm{3}}\centerdot\mathrm{120}=\mathrm{80} \\ $$$$\mathrm{3}^{{n}} =\mathrm{81} \\ $$$$\mathrm{3}^{{n}} =\mathrm{3}^{\mathrm{4}} \\ $$$${n}=\mathrm{4} \\ $$$$\mathrm{3}+\mathrm{9}+\mathrm{27}+\mathrm{81}=\mathrm{120} \\ $$

Pin