Menu Close

Is-the-sequence-u-n-defined-by-the-formula-u-n-n-1-5-n-lgn-where-n-Z-n-2-convergent-If-so-find-its-sum-as-n-

Tinku Tara
Pin




Question Number 408 by 112358 last updated on 30/Dec/14
Is the sequence {u_n } defined by the formula u_n =((n+(−1.5)^n )/(lgn)) , where n∈Z^+ ∣n≥2 , convergent? If so find its sum as n→∞.
$${Is}\:{the}\:{sequence}\:\left\{{u}_{{n}} \right\}\:{defined}\:{by}\:{the}\:{formula}\:{u}_{{n}} =\frac{{n}+\left(−\mathrm{1}.\mathrm{5}\right)^{{n}} }{{lgn}}\:,\:{where}\:{n}\in{Z}^{+} \mid{n}\geqslant\mathrm{2}\:,\:{convergent}?\:{If}\:{so}\:{find}\:{its}\:{sum}\:{as}\:{n}\rightarrow\infty. \\ $$
Commented by 123456 last updated on 30/Dec/14
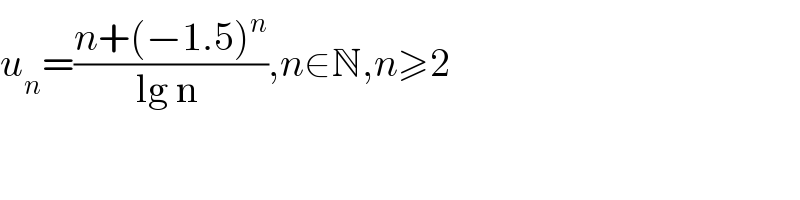
u_n =((n+(−1.5)^n )/(lg n )),n∈N,n≥2
$${u}_{{n}} =\frac{{n}+\left(−\mathrm{1}.\mathrm{5}\right)^{{n}} }{\mathrm{lg}\:\mathrm{n}\:},{n}\in\mathbb{N},{n}\geqslant\mathrm{2} \\ $$
Commented by 123456 last updated on 30/Dec/14
((∞±∞)/∞) (?/∞),(∞/∞)
$$\frac{\infty\pm\infty}{\infty} \\ $$$$\frac{?}{\infty},\frac{\infty}{\infty} \\ $$
Commented by prakash jain last updated on 31/Dec/14
u_n =((n+(−1.5)^n )/(lg n)) u_(2k) =((2k+(1.5)^(2k) )/(lg 2k)) u_(2k+1) =(((2k+1)−(1.5)^(2k+1) )/(lg (2k+1))) We can define a sequence with i^(th ) element v_i given by i≥1 v_i =u_(2i) +u_(2i+1) v_i =((2i)/(lg 2i))+((2i+1)/(lg (2i+1)))+(((1.5)^(2i) )/(lg 2i))−(((1.5)^(2i+1) )/(lg (2i+1)))
$${u}_{{n}} =\frac{{n}+\left(−\mathrm{1}.\mathrm{5}\right)^{{n}} }{\mathrm{lg}\:{n}} \\ $$$${u}_{\mathrm{2}{k}} =\frac{\mathrm{2}{k}+\left(\mathrm{1}.\mathrm{5}\right)^{\mathrm{2}{k}} }{\mathrm{lg}\:\mathrm{2}{k}} \\ $$$${u}_{\mathrm{2}{k}+\mathrm{1}} =\frac{\left(\mathrm{2}{k}+\mathrm{1}\right)−\left(\mathrm{1}.\mathrm{5}\right)^{\mathrm{2}{k}+\mathrm{1}} }{\mathrm{lg}\:\left(\mathrm{2}{k}+\mathrm{1}\right)} \\ $$$$\mathrm{We}\:\mathrm{can}\:\mathrm{define}\:\mathrm{a}\:\mathrm{sequence}\:\mathrm{with}\:{i}^{{th}\:} \mathrm{element}\:{v}_{{i}} \\ $$$$\mathrm{given}\:\mathrm{by}\:{i}\geqslant\mathrm{1} \\ $$$${v}_{{i}} ={u}_{\mathrm{2}{i}} +{u}_{\mathrm{2}{i}+\mathrm{1}} \\ $$$${v}_{{i}} =\frac{\mathrm{2}{i}}{\mathrm{lg}\:\mathrm{2}{i}}+\frac{\mathrm{2}{i}+\mathrm{1}}{\mathrm{lg}\:\left(\mathrm{2}{i}+\mathrm{1}\right)}+\frac{\left(\mathrm{1}.\mathrm{5}\right)^{\mathrm{2}{i}} }{\mathrm{lg}\:\mathrm{2}{i}}−\frac{\left(\mathrm{1}.\mathrm{5}\right)^{\mathrm{2}{i}+\mathrm{1}} }{\mathrm{lg}\:\left(\mathrm{2}{i}+\mathrm{1}\right)} \\ $$

Pin