Menu Close

Knowing-that-e-i-1-1-i-Show-that-e-is-finite-That-is-show-the-following-is-true-S-x-R-x-lt-e-x-Where-S-is-the-solution-

Tinku Tara 0 Comments
Pin




Question Number 2791 by Filup last updated on 27/Nov/15
Knowing that e=Σ_(i=1) ^∞ (1/(i!)), Show that e is finite. That is, show the following is true: S={∃x∈R:∣x∣<∞, e=x} Where S is the solution
$$\mathrm{Knowing}\:\mathrm{that}\:{e}=\underset{{i}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{{i}!}, \\ $$$$\mathrm{Show}\:\mathrm{that}\:{e}\:\mathrm{is}\:\mathrm{finite}. \\ $$$$ \\ $$$$\mathrm{That}\:\mathrm{is},\:\mathrm{show}\:\mathrm{the}\:\mathrm{following}\:\mathrm{is}\:\mathrm{true}: \\ $$$${S}=\left\{\exists{x}\in\mathbb{R}:\mid{x}\mid<\infty,\:{e}={x}\right\} \\ $$$$\mathrm{Where}\:{S}\:\mathrm{is}\:\mathrm{the}\:\mathrm{solution} \\ $$
Commented by prakash jain last updated on 27/Nov/15
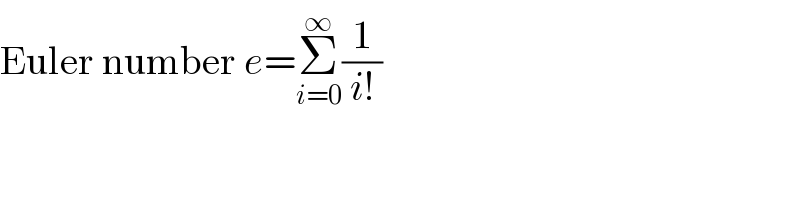
Euler number e=Σ_(i=0) ^∞ (1/(i!))
$$\mathrm{Euler}\:\mathrm{number}\:{e}=\underset{{i}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{{i}!} \\ $$
Answered by prakash jain last updated on 27/Nov/15
e=(1/(1!))+(1/(2!))+(1/(3!))+.. e=1+...⇒ e>1 remain terms (1/(2!))+(1/(3!))+(1/(4!))+... 2!=2 3!>2^2 ⇒(1/(3!))<(1/2^2 ) Similary (1/(4!))<(1/2^3 ) (1/(2!))+(1/(3!))+(1/(4!))+...<(1/2)+(1/2^2 )+(1/2^3 )=((1/2)/(1−1/2))=1 e<1+1=2 1<e<2 Hence S is true. Note that e in your question is not THE constant e.
$${e}=\frac{\mathrm{1}}{\mathrm{1}!}+\frac{\mathrm{1}}{\mathrm{2}!}+\frac{\mathrm{1}}{\mathrm{3}!}+.. \\ $$$${e}=\mathrm{1}+…\Rightarrow\:{e}>\mathrm{1} \\ $$$$\mathrm{remain}\:\mathrm{terms} \\ $$$$\frac{\mathrm{1}}{\mathrm{2}!}+\frac{\mathrm{1}}{\mathrm{3}!}+\frac{\mathrm{1}}{\mathrm{4}!}+… \\ $$$$\mathrm{2}!=\mathrm{2} \\ $$$$\mathrm{3}!>\mathrm{2}^{\mathrm{2}} \Rightarrow\frac{\mathrm{1}}{\mathrm{3}!}<\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{2}} } \\ $$$$\mathrm{Similary}\:\frac{\mathrm{1}}{\mathrm{4}!}<\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{3}} } \\ $$$$\frac{\mathrm{1}}{\mathrm{2}!}+\frac{\mathrm{1}}{\mathrm{3}!}+\frac{\mathrm{1}}{\mathrm{4}!}+…<\frac{\mathrm{1}}{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{2}} }+\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{3}} }=\frac{\mathrm{1}/\mathrm{2}}{\mathrm{1}−\mathrm{1}/\mathrm{2}}=\mathrm{1} \\ $$$${e}<\mathrm{1}+\mathrm{1}=\mathrm{2} \\ $$$$\mathrm{1}<{e}<\mathrm{2} \\ $$$$\mathrm{Hence}\:{S}\:\mathrm{is}\:\mathrm{true}. \\ $$$$\mathrm{Note}\:\mathrm{that}\:{e}\:\mathrm{in}\:\mathrm{your}\:\mathrm{question}\:\mathrm{is}\:\mathrm{not}\:\mathrm{THE} \\ $$$$\mathrm{constant}\:\boldsymbol{{e}}. \\ $$
Commented by Filup last updated on 27/Nov/15
Oh. Its a typo. It was meant to be the constant. Nice proof, regardless!
$$\mathrm{O}{h}.\:\mathrm{Its}\:\mathrm{a}\:\mathrm{typo}.\:\mathrm{It}\:\mathrm{was}\:\mathrm{meant}\:\mathrm{to}\:\mathrm{be}\:\mathrm{the} \\ $$$$\mathrm{constant}.\:\mathrm{Nice}\:\mathrm{proof},\:{regardless}! \\ $$
Commented by prakash jain last updated on 27/Nov/15
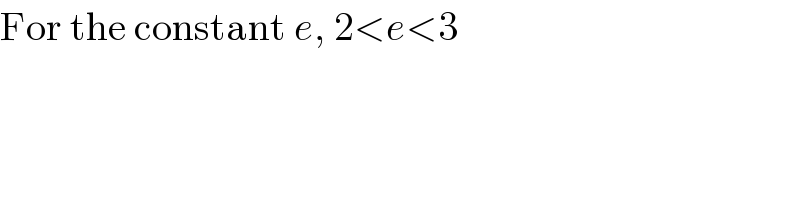
For the constant e, 2<e<3
$$\mathrm{For}\:\mathrm{the}\:\mathrm{constant}\:{e},\:\mathrm{2}<{e}<\mathrm{3} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *