Question Number 65773 by mathmax by abdo last updated on 03/Aug/19
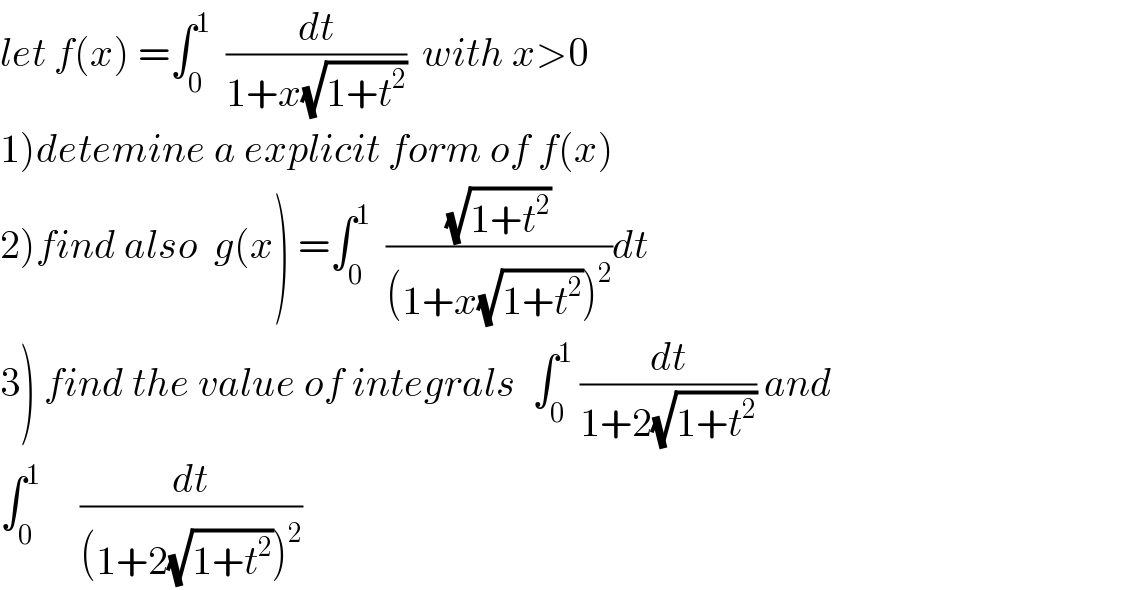
$${let}\:{f}\left({x}\right)\:=\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\frac{{dt}}{\mathrm{1}+{x}\sqrt{\mathrm{1}+{t}^{\mathrm{2}} }}\:\:{with}\:{x}>\mathrm{0} \\ $$$$\left.\mathrm{1}\right){detemine}\:{a}\:{explicit}\:{form}\:{of}\:{f}\left({x}\right) \\ $$$$\left.\mathrm{2}\right){find}\:{also}\:\:{g}\left({x}\right)\:=\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\frac{\sqrt{\mathrm{1}+{t}^{\mathrm{2}} }}{\left(\mathrm{1}+{x}\sqrt{\mathrm{1}+{t}^{\mathrm{2}} }\right)^{\mathrm{2}} }{dt} \\ $$$$\left.\mathrm{3}\right)\:{find}\:{the}\:{value}\:{of}\:{integrals}\:\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{{dt}}{\mathrm{1}+\mathrm{2}\sqrt{\mathrm{1}+{t}^{\mathrm{2}} }}\:{and}\: \\ $$$$\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\:\:\:\frac{{dt}}{\left(\mathrm{1}+\mathrm{2}\sqrt{\mathrm{1}+{t}^{\mathrm{2}} }\right)^{\mathrm{2}} } \\ $$
Commented by mathmax by abdo last updated on 06/Aug/19
![2)we have f^′ (x) =−∫_0 ^1 (((√(1+t^2 ))dt)/((1+x(√(1+t^2 )))^2 )) =−g(x) ⇒g(x)=−f^′ (x) rest to calculate f^′ (x) 3)changement t =sht give I=∫_0 ^1 (dt/(1+2(√(1+t^2 )))) =∫_0 ^(ln(1+(√2))) ((ch(t)dt)/(1+2ch(t))) =∫_0 ^(ln(1+(√2))) (((e^t +e^(−t) )/2)/(1+2((e^t +e^(−t) )/2)))dt =(1/2)∫_0 ^(ln(1+(√2))) ((e^t +e^(−t) )/(1+e^t +e^(−t) ))dt =_(e^t =x) (1/2)∫_1 ^(1+(√2)) ((x+x^(−1) )/(1+x+x^(−1) ))(dx/x) =(1/2) ∫_1 ^(1+(√2)) ((x^2 +1)/(x^2 (1+x+x^(−1) )))dx =(1/2)∫_1 ^(1+(√2)) ((x^2 +1)/(x^2 +x^3 +x))dx =(1/2)∫_1 ^(1+(√2)) ((x^2 +1)/(x(x^2 +x+1)))dx let decomposeF(x)=((x^2 +1)/(x(x^2 +x+1))) F(x) =(a/x) +((bx+c)/(x^2 +x+1)) a =lim_(x→0) xF(x) =1 lim_(x→+∞) xF(x) =1 =a+b ⇒b=1−a=0 ⇒F(x)=(1/x) +(c/(x^2 +x+1)) F(1) =(2/3) =1 +(c/3) ⇒2 =3 +c ⇒c =−1⇒F(x)=(1/x)−(1/(x^2 +x+1)) ⇒ I =(1/2){ ∫_1 ^(1+(√2)) (dx/x)−∫_1 ^(1+(√2)) (dx/(x^2 +x+1))} =(1/2)ln(1+(√2))−(1/2)∫_1 ^(1+(√2)) (dx/(x^2 +x+1)) ∫_1 ^(1+(√2)) (dx/(x^2 +x+1)) =∫_1 ^(1+(√2)) (dx/((x+(1/2))^2 +(3/4))) =_(x+(1/2)=((√3)/2)u) (4/3) ∫_(√3) ^((3+2(√2))/3) (1/(1+u^2 ))((√3)/2)du = (2/( (√3))) [arctanu]_(√3) ^((3+2(√2))/3) =(2/( (√3))){ arctan(((3+2(√2))/3))−arctan((√3))}⇒ I =(1/2)ln(1+(√2))−(1/( (√3))){arctan(((3+2(√2))/3))−arctan((√3))}](https://www.tinkutara.com/question/Q65965.png)
$$\left.\mathrm{2}\right){we}\:{have}\:{f}^{'} \left({x}\right)\:=−\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\frac{\sqrt{\mathrm{1}+{t}^{\mathrm{2}} }{dt}}{\left(\mathrm{1}+{x}\sqrt{\mathrm{1}+{t}^{\mathrm{2}} }\right)^{\mathrm{2}} }\:=−{g}\left({x}\right)\:\Rightarrow{g}\left({x}\right)=−{f}^{'} \left({x}\right) \\ $$$${rest}\:{to}\:{calculate}\:{f}^{'} \left({x}\right) \\ $$$$\left.\mathrm{3}\right){changement}\:{t}\:={sht}\:{give}\:{I}=\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{{dt}}{\mathrm{1}+\mathrm{2}\sqrt{\mathrm{1}+{t}^{\mathrm{2}} }} \\ $$$$=\int_{\mathrm{0}} ^{{ln}\left(\mathrm{1}+\sqrt{\mathrm{2}}\right)} \:\:\:\frac{{ch}\left({t}\right){dt}}{\mathrm{1}+\mathrm{2}{ch}\left({t}\right)}\:=\int_{\mathrm{0}} ^{{ln}\left(\mathrm{1}+\sqrt{\mathrm{2}}\right)} \:\:\frac{\frac{{e}^{{t}} \:+{e}^{−{t}} }{\mathrm{2}}}{\mathrm{1}+\mathrm{2}\frac{{e}^{{t}} \:+{e}^{−{t}} }{\mathrm{2}}}{dt} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{{ln}\left(\mathrm{1}+\sqrt{\mathrm{2}}\right)} \:\:\:\frac{{e}^{{t}} \:+{e}^{−{t}} }{\mathrm{1}+{e}^{{t}} \:+{e}^{−{t}} }{dt}\:\:=_{{e}^{{t}} ={x}} \:\:\:\:\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{1}} ^{\mathrm{1}+\sqrt{\mathrm{2}}} \:\:\:\frac{{x}+{x}^{−\mathrm{1}} }{\mathrm{1}+{x}+{x}^{−\mathrm{1}} }\frac{{dx}}{{x}} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\:\int_{\mathrm{1}} ^{\mathrm{1}+\sqrt{\mathrm{2}}} \:\:\:\frac{{x}^{\mathrm{2}} \:+\mathrm{1}}{{x}^{\mathrm{2}} \left(\mathrm{1}+{x}+{x}^{−\mathrm{1}} \right)}{dx}\:=\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{1}} ^{\mathrm{1}+\sqrt{\mathrm{2}}} \:\:\frac{{x}^{\mathrm{2}} \:+\mathrm{1}}{{x}^{\mathrm{2}} \:+{x}^{\mathrm{3}} \:+{x}}{dx} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{1}} ^{\mathrm{1}+\sqrt{\mathrm{2}}} \:\:\:\frac{{x}^{\mathrm{2}} \:+\mathrm{1}}{{x}\left({x}^{\mathrm{2}} \:+{x}+\mathrm{1}\right)}{dx}\:\:{let}\:{decomposeF}\left({x}\right)=\frac{{x}^{\mathrm{2}} \:+\mathrm{1}}{{x}\left({x}^{\mathrm{2}} \:+{x}+\mathrm{1}\right)} \\ $$$${F}\left({x}\right)\:=\frac{{a}}{{x}}\:+\frac{{bx}+{c}}{{x}^{\mathrm{2}} \:+{x}+\mathrm{1}} \\ $$$${a}\:={lim}_{{x}\rightarrow\mathrm{0}} {xF}\left({x}\right)\:=\mathrm{1} \\ $$$${lim}_{{x}\rightarrow+\infty} {xF}\left({x}\right)\:=\mathrm{1}\:={a}+{b}\:\Rightarrow{b}=\mathrm{1}−{a}=\mathrm{0}\:\Rightarrow{F}\left({x}\right)=\frac{\mathrm{1}}{{x}}\:+\frac{{c}}{{x}^{\mathrm{2}} \:+{x}+\mathrm{1}} \\ $$$${F}\left(\mathrm{1}\right)\:=\frac{\mathrm{2}}{\mathrm{3}}\:=\mathrm{1}\:+\frac{{c}}{\mathrm{3}}\:\Rightarrow\mathrm{2}\:=\mathrm{3}\:+{c}\:\Rightarrow{c}\:=−\mathrm{1}\Rightarrow{F}\left({x}\right)=\frac{\mathrm{1}}{{x}}−\frac{\mathrm{1}}{{x}^{\mathrm{2}} \:+{x}+\mathrm{1}} \\ $$$$\Rightarrow\:{I}\:=\frac{\mathrm{1}}{\mathrm{2}}\left\{\:\int_{\mathrm{1}} ^{\mathrm{1}+\sqrt{\mathrm{2}}} \frac{{dx}}{{x}}−\int_{\mathrm{1}} ^{\mathrm{1}+\sqrt{\mathrm{2}}} \:\:\frac{{dx}}{{x}^{\mathrm{2}} \:+{x}+\mathrm{1}}\right\} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}{ln}\left(\mathrm{1}+\sqrt{\mathrm{2}}\right)−\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{1}} ^{\mathrm{1}+\sqrt{\mathrm{2}}} \:\:\frac{{dx}}{{x}^{\mathrm{2}} \:+{x}+\mathrm{1}} \\ $$$$\int_{\mathrm{1}} ^{\mathrm{1}+\sqrt{\mathrm{2}}} \:\:\frac{{dx}}{{x}^{\mathrm{2}} \:+{x}+\mathrm{1}}\:=\int_{\mathrm{1}} ^{\mathrm{1}+\sqrt{\mathrm{2}}} \:\:\frac{{dx}}{\left({x}+\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} \:+\frac{\mathrm{3}}{\mathrm{4}}}\:=_{{x}+\frac{\mathrm{1}}{\mathrm{2}}=\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}{u}} \:\frac{\mathrm{4}}{\mathrm{3}}\:\:\int_{\sqrt{\mathrm{3}}} ^{\frac{\mathrm{3}+\mathrm{2}\sqrt{\mathrm{2}}}{\mathrm{3}}} \:\frac{\mathrm{1}}{\mathrm{1}+{u}^{\mathrm{2}} }\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}{du} \\ $$$$=\:\frac{\mathrm{2}}{\:\sqrt{\mathrm{3}}}\:\left[{arctanu}\right]_{\sqrt{\mathrm{3}}} ^{\frac{\mathrm{3}+\mathrm{2}\sqrt{\mathrm{2}}}{\mathrm{3}}} \:=\frac{\mathrm{2}}{\:\sqrt{\mathrm{3}}}\left\{\:{arctan}\left(\frac{\mathrm{3}+\mathrm{2}\sqrt{\mathrm{2}}}{\mathrm{3}}\right)−{arctan}\left(\sqrt{\mathrm{3}}\right)\right\}\Rightarrow \\ $$$${I}\:=\frac{\mathrm{1}}{\mathrm{2}}{ln}\left(\mathrm{1}+\sqrt{\mathrm{2}}\right)−\frac{\mathrm{1}}{\:\sqrt{\mathrm{3}}}\left\{{arctan}\left(\frac{\mathrm{3}+\mathrm{2}\sqrt{\mathrm{2}}}{\mathrm{3}}\right)−{arctan}\left(\sqrt{\mathrm{3}}\right)\right\} \\ $$$$ \\ $$
Commented by mathmax by abdo last updated on 06/Aug/19
![1)f(x) =∫_0 ^1 (dt/(1+x(√(1+t^2 )))) changement t =sh(u) give f(x)=∫_0 ^(ln(1+(√2))) ((chu)/(1+xchu))du =∫_0 ^(ln(1+(√2))) (((e^u +e^(−u) )/2)/(1+x((e^u +e^(−u) )/2)))du = ∫_0 ^(ln(1+(√2))) ((e^u +e^(−u) )/(2 +xe^u +x e^(−u) )) du =_(e^u =z) ∫_1 ^(1+(√2)) ((z+z^(−1) )/(2+xz+xz^(−1) ))(dz/z) = ∫_1 ^(1+(√2)) ((z^2 +1)/(z^2 (2+xz +xz^(−1) )))dz =∫_1 ^(1+(√2)) ((z^2 +1)/(2z^2 +xz^3 +xz))dz =∫_1 ^(1+(√2)) ((z^2 +1)/(z(xz^2 +2z+x)))dz let decomposeF(z) =((z^2 +1)/(z(xz^2 +2z+x))) xz^2 +2z +x =0 →Δ^′ =1−x^2 case 1 1−x^2 >0 ⇒0<x<1 ⇒z_1 =((−1+(√(1−x^2 )))/x) z_2 =((−1−(√(1−x^2 )))/x) ⇒F(z) =((z^2 +1)/(xz(z−z_1 )(z−z_2 ))) =(a/z) +(b/(z−z_1 )) +(c/(z−z_2 )) a =lim_(z→0) zF(z) =(1/x) b =lim_(z→z_1 ) (z−z_1 )F(z) =((z_1 ^2 +1)/(xz_1 (z_1 −z_2 ))) c =lim_(z→z_2 ) (z−z_2 )F(z) =((z_2 ^2 +1)/(xz_2 (z_2 −z_1 ))) ⇒ f(x) =∫_1 ^(1+(√2)) F(z)dz =[aln∣z∣+bln∣z−z_1 ∣+cln∣z−z_2 ∣]_1 ^(1+(√2)) =aln(1+(√2))+bln∣1+(√2)−z_1 ∣+cln∣1+(√2)−z_2 ∣−bln∣1−z_1 ∣ −cln∣1−z_2 ∣ case 2 1−x^2 <0 ⇒x>1 f(x)=∫_1 ^(1+(√2)) ((z^2 +1)/(z(xz^2 +2z +x)))dz F(z) =(a/z) +((bz +c)/(xz^2 +2z +x)) a =(1/x) lim_(z→+∞) zF(z) =(1/x) =a+(b/x) ⇒1 =ax +b ⇒b=1−ax=0 ⇒ F(z) =(1/(xz)) +(c/(xz^2 +2z +x)) F(1) =(2/((2x+2))) =(1/(x+1)) =(1/x) +(c/(2x+2)) ⇒1 =((x+1)/x) +(c/2) ⇒ (c/2) =−(1/x) ⇒c =((−2)/x) ⇒ F(z) =(1/(xz))−(2/x)(1/((xz^2 +2z +x))) =(1/x){ (1/z)−(2/(xz^2 +2z +x))} ⇒f(x) =(1/x){ ∫_1 ^(1+(√2)) (dz/z)−2∫_1 ^(1+(√2)) (dz/(xz^2 +2z+x))} =(1/x)ln(1+(√2))−(2/x) ∫_1 ^(1+(√2)) (dz/(xz^2 +2z +x)) =....](https://www.tinkutara.com/question/Q65957.png)
$$\left.\mathrm{1}\right){f}\left({x}\right)\:=\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\frac{{dt}}{\mathrm{1}+{x}\sqrt{\mathrm{1}+{t}^{\mathrm{2}} }}\:\:{changement}\:{t}\:={sh}\left({u}\right)\:{give} \\ $$$${f}\left({x}\right)=\int_{\mathrm{0}} ^{{ln}\left(\mathrm{1}+\sqrt{\mathrm{2}}\right)} \:\:\frac{{chu}}{\mathrm{1}+{xchu}}{du}\:=\int_{\mathrm{0}} ^{{ln}\left(\mathrm{1}+\sqrt{\mathrm{2}}\right)} \:\:\:\frac{\frac{{e}^{{u}} +{e}^{−{u}} }{\mathrm{2}}}{\mathrm{1}+{x}\frac{{e}^{{u}} +{e}^{−{u}} }{\mathrm{2}}}{du} \\ $$$$=\:\int_{\mathrm{0}} ^{{ln}\left(\mathrm{1}+\sqrt{\mathrm{2}}\right)} \:\:\:\:\frac{{e}^{{u}} +{e}^{−{u}} }{\mathrm{2}\:+{xe}^{{u}} \:+{x}\:{e}^{−{u}} }\:{du}\:\:=_{{e}^{{u}} ={z}} \:\:\:\int_{\mathrm{1}} ^{\mathrm{1}+\sqrt{\mathrm{2}}} \frac{{z}+{z}^{−\mathrm{1}} }{\mathrm{2}+{xz}+{xz}^{−\mathrm{1}} }\frac{{dz}}{{z}} \\ $$$$=\:\int_{\mathrm{1}} ^{\mathrm{1}+\sqrt{\mathrm{2}}} \:\:\:\:\:\frac{{z}^{\mathrm{2}} \:+\mathrm{1}}{{z}^{\mathrm{2}} \left(\mathrm{2}+{xz}\:+{xz}^{−\mathrm{1}} \right)}{dz}\:=\int_{\mathrm{1}} ^{\mathrm{1}+\sqrt{\mathrm{2}}} \:\:\frac{{z}^{\mathrm{2}} \:+\mathrm{1}}{\mathrm{2}{z}^{\mathrm{2}} \:+{xz}^{\mathrm{3}} \:+{xz}}{dz} \\ $$$$=\int_{\mathrm{1}} ^{\mathrm{1}+\sqrt{\mathrm{2}}} \:\:\frac{{z}^{\mathrm{2}} \:+\mathrm{1}}{{z}\left({xz}^{\mathrm{2}} \:+\mathrm{2}{z}+{x}\right)}{dz}\:{let}\:{decomposeF}\left({z}\right)\:=\frac{{z}^{\mathrm{2}} \:+\mathrm{1}}{{z}\left({xz}^{\mathrm{2}} \:+\mathrm{2}{z}+{x}\right)} \\ $$$${xz}^{\mathrm{2}} \:+\mathrm{2}{z}\:+{x}\:=\mathrm{0}\:\rightarrow\Delta^{'} \:=\mathrm{1}−{x}^{\mathrm{2}} \\ $$$${case}\:\mathrm{1}\:\:\mathrm{1}−{x}^{\mathrm{2}} >\mathrm{0}\:\Rightarrow\mathrm{0}<{x}<\mathrm{1}\:\Rightarrow{z}_{\mathrm{1}} =\frac{−\mathrm{1}+\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }}{{x}} \\ $$$${z}_{\mathrm{2}} =\frac{−\mathrm{1}−\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }}{{x}}\:\Rightarrow{F}\left({z}\right)\:=\frac{{z}^{\mathrm{2}} \:+\mathrm{1}}{{xz}\left({z}−{z}_{\mathrm{1}} \right)\left({z}−{z}_{\mathrm{2}} \right)} \\ $$$$=\frac{{a}}{{z}}\:+\frac{{b}}{{z}−{z}_{\mathrm{1}} }\:+\frac{{c}}{{z}−{z}_{\mathrm{2}} } \\ $$$${a}\:={lim}_{{z}\rightarrow\mathrm{0}} {zF}\left({z}\right)\:=\frac{\mathrm{1}}{{x}} \\ $$$${b}\:={lim}_{{z}\rightarrow{z}_{\mathrm{1}} } \:\:\left({z}−{z}_{\mathrm{1}} \right){F}\left({z}\right)\:=\frac{{z}_{\mathrm{1}} ^{\mathrm{2}} \:+\mathrm{1}}{{xz}_{\mathrm{1}} \left({z}_{\mathrm{1}} −{z}_{\mathrm{2}} \right)}\: \\ $$$${c}\:={lim}_{{z}\rightarrow{z}_{\mathrm{2}} } \:\:\left({z}−{z}_{\mathrm{2}} \right){F}\left({z}\right)\:=\frac{{z}_{\mathrm{2}} ^{\mathrm{2}} \:+\mathrm{1}}{{xz}_{\mathrm{2}} \left({z}_{\mathrm{2}} −{z}_{\mathrm{1}} \right)}\:\Rightarrow \\ $$$${f}\left({x}\right)\:=\int_{\mathrm{1}} ^{\mathrm{1}+\sqrt{\mathrm{2}}} {F}\left({z}\right){dz}\:=\left[{aln}\mid{z}\mid+{bln}\mid{z}−{z}_{\mathrm{1}} \mid+{cln}\mid{z}−{z}_{\mathrm{2}} \mid\right]_{\mathrm{1}} ^{\mathrm{1}+\sqrt{\mathrm{2}}} \\ $$$$={aln}\left(\mathrm{1}+\sqrt{\mathrm{2}}\right)+{bln}\mid\mathrm{1}+\sqrt{\mathrm{2}}−{z}_{\mathrm{1}} \mid+{cln}\mid\mathrm{1}+\sqrt{\mathrm{2}}−{z}_{\mathrm{2}} \mid−{bln}\mid\mathrm{1}−{z}_{\mathrm{1}} \mid \\ $$$$−{cln}\mid\mathrm{1}−{z}_{\mathrm{2}} \mid \\ $$$${case}\:\mathrm{2}\:\:\mathrm{1}−{x}^{\mathrm{2}} <\mathrm{0}\:\Rightarrow{x}>\mathrm{1}\:\:{f}\left({x}\right)=\int_{\mathrm{1}} ^{\mathrm{1}+\sqrt{\mathrm{2}}} \:\frac{{z}^{\mathrm{2}} \:+\mathrm{1}}{{z}\left({xz}^{\mathrm{2}} \:+\mathrm{2}{z}\:+{x}\right)}{dz} \\ $$$${F}\left({z}\right)\:=\frac{{a}}{{z}}\:+\frac{{bz}\:+{c}}{{xz}^{\mathrm{2}} \:+\mathrm{2}{z}\:+{x}} \\ $$$${a}\:=\frac{\mathrm{1}}{{x}} \\ $$$${lim}_{{z}\rightarrow+\infty} \:{zF}\left({z}\right)\:=\frac{\mathrm{1}}{{x}}\:={a}+\frac{{b}}{{x}}\:\Rightarrow\mathrm{1}\:={ax}\:+{b}\:\Rightarrow{b}=\mathrm{1}−{ax}=\mathrm{0}\:\Rightarrow \\ $$$${F}\left({z}\right)\:=\frac{\mathrm{1}}{{xz}}\:+\frac{{c}}{{xz}^{\mathrm{2}} \:+\mathrm{2}{z}\:+{x}} \\ $$$${F}\left(\mathrm{1}\right)\:=\frac{\mathrm{2}}{\left(\mathrm{2}{x}+\mathrm{2}\right)}\:=\frac{\mathrm{1}}{{x}+\mathrm{1}}\:=\frac{\mathrm{1}}{{x}}\:+\frac{{c}}{\mathrm{2}{x}+\mathrm{2}}\:\Rightarrow\mathrm{1}\:=\frac{{x}+\mathrm{1}}{{x}}\:+\frac{{c}}{\mathrm{2}}\:\Rightarrow \\ $$$$\frac{{c}}{\mathrm{2}}\:=−\frac{\mathrm{1}}{{x}}\:\Rightarrow{c}\:=\frac{−\mathrm{2}}{{x}}\:\Rightarrow\:{F}\left({z}\right)\:=\frac{\mathrm{1}}{{xz}}−\frac{\mathrm{2}}{{x}}\frac{\mathrm{1}}{\left({xz}^{\mathrm{2}} \:+\mathrm{2}{z}\:+{x}\right)} \\ $$$$=\frac{\mathrm{1}}{{x}}\left\{\:\frac{\mathrm{1}}{{z}}−\frac{\mathrm{2}}{{xz}^{\mathrm{2}} \:+\mathrm{2}{z}\:+{x}}\right\}\:\Rightarrow{f}\left({x}\right)\:=\frac{\mathrm{1}}{{x}}\left\{\:\int_{\mathrm{1}} ^{\mathrm{1}+\sqrt{\mathrm{2}}} \:\frac{{dz}}{{z}}−\mathrm{2}\int_{\mathrm{1}} ^{\mathrm{1}+\sqrt{\mathrm{2}}} \:\frac{{dz}}{{xz}^{\mathrm{2}} \:+\mathrm{2}{z}+{x}}\right\} \\ $$$$=\frac{\mathrm{1}}{{x}}{ln}\left(\mathrm{1}+\sqrt{\mathrm{2}}\right)−\frac{\mathrm{2}}{{x}}\:\int_{\mathrm{1}} ^{\mathrm{1}+\sqrt{\mathrm{2}}} \:\:\:\:\frac{{dz}}{{xz}^{\mathrm{2}} \:+\mathrm{2}{z}\:+{x}}\:=…. \\ $$$$ \\ $$
