Question Number 66062 by mathmax by abdo last updated on 08/Aug/19
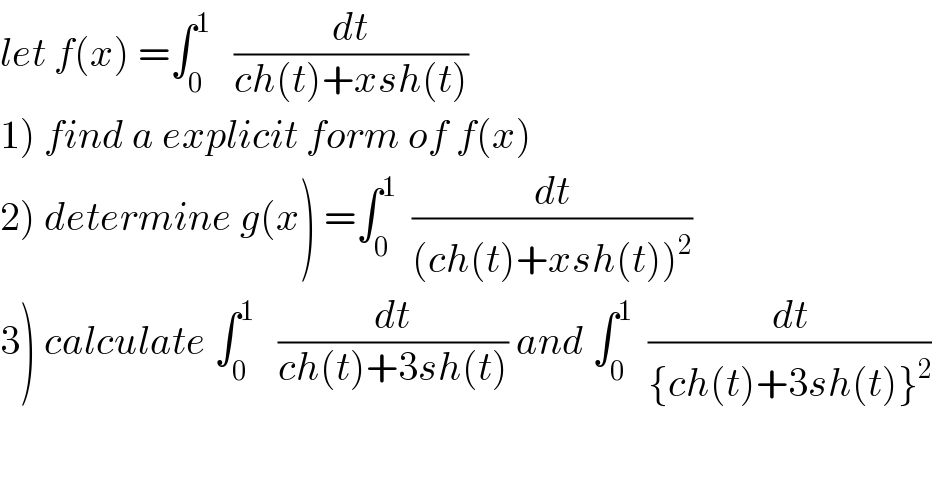
$${let}\:{f}\left({x}\right)\:=\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\:\frac{{dt}}{{ch}\left({t}\right)+{xsh}\left({t}\right)} \\ $$$$\left.\mathrm{1}\right)\:{find}\:{a}\:{explicit}\:{form}\:{of}\:{f}\left({x}\right) \\ $$$$\left.\mathrm{2}\right)\:{determine}\:{g}\left({x}\right)\:=\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\frac{{dt}}{\left({ch}\left({t}\right)+{xsh}\left({t}\right)\right)^{\mathrm{2}} } \\ $$$$\left.\mathrm{3}\right)\:{calculate}\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\:\frac{{dt}}{{ch}\left({t}\right)+\mathrm{3}{sh}\left({t}\right)}\:{and}\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\frac{{dt}}{\left\{{ch}\left({t}\right)+\mathrm{3}{sh}\left({t}\right)\right\}^{\mathrm{2}} } \\ $$
Commented by mathmax by abdo last updated on 11/Aug/19
![1) we have f(x)=∫_0 ^1 (dt/(ch(t)+xsh(t))) ⇒ f(x)=∫_0 ^1 ((2dt)/(e^t +e^(−t) +x(e^t −e^(−t) ))) =∫_0 ^1 ((2dt)/((1+x)e^t +(1−x)e^(−t) )) changement e^t =u give f(x)=∫_1 ^e (2/((1+x)u +(1−x)u^(−1) ))(du/u) =∫_1 ^e ((2du)/((1+x)u^2 +(1−x))) =(2/(1+x)) ∫_1 ^e (du/(u^2 +((1−x)/(1+x)))) case 1 ((1−x)/(1+x))>0 ⇒∣x∣<1 we do the changement u=(√((1−x)/(1+x)))z ⇒ f(x) =(2/(1+x)) ∫_(√((1+x)/(1−x))) ^(e(√((1+x)/(1−x)))) ((1+x)/(1−x)) (1/(1+z^2 )) (√((1−x)/(1+x)))dz =(2/(1−x))((√(1−x))/( (√(1+x)))) [arctan(z)]_(√((1+x)/(1−x))) ^(e(√((1+x)/(1−x)))) =(2/( (√(1−x^2 )))){ arctan(e(√((1+x)/(1−x))))−arctan((√((1+x)/(1−x))))} case 2 ((1−x)/(1−x))<0 ⇒∣x∣>1 ⇒f(x)=(2/(x+1)) ∫_1 ^e (du/(u^2 −((√((x−1)/(x+1))))^2 )) =_(u=(√((x−1)/(x+1)))z) (2/(x+1)) ∫_(√((x+1)/(x−1))) ^(e(√((x+1)/(x−1)))) ((x+1)/(x−1)) (1/(z^2 −1))(√((x−1)/(x+1)))dz =(1/(x−1))((√(x−1))/( (√(x+1)))) ∫_(√((x+1)/(x−1))) ^(e(√((x+1)/(x−1)))) {(1/(z−1))−(1/(z+1))}dz =(1/( (√(x^2 −1))))[ln∣((z−1)/(z+1))∣]_(√((x+1)/(x−1))) ^(e(√((x+1)/(x−1)))) =(1/( (√(x^2 −1)))){ln∣((((e(√(x+1)))/( (√(x−1))))−1)/(((e(√(x+1)))/( (√(x−1))))+1))∣ −ln∣((((√(x+1))/( (√(x−1))))−1)/(((√(x+1))/( (√(x−1))))+1))∣} ⇒ f(x)=(1/( (√(x^2 −1)))){ln∣((e(√(x+1))−(√(x−1)))/(e(√(x+1))+(√(x−1))))∣−ln∣(((√(x+1))−(√(x−1)))/( (√(x+1))+(√(x−1))))∣}](https://www.tinkutara.com/question/Q66246.png)
$$\left.\mathrm{1}\right)\:{we}\:{have}\:{f}\left({x}\right)=\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{{dt}}{{ch}\left({t}\right)+{xsh}\left({t}\right)}\:\Rightarrow \\ $$$${f}\left({x}\right)=\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\frac{\mathrm{2}{dt}}{{e}^{{t}} \:+{e}^{−{t}} \:+{x}\left({e}^{{t}} −{e}^{−{t}} \right)}\:=\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{\mathrm{2}{dt}}{\left(\mathrm{1}+{x}\right){e}^{{t}} \:+\left(\mathrm{1}−{x}\right){e}^{−{t}} } \\ $$$${changement}\:{e}^{{t}} ={u}\:{give}\:{f}\left({x}\right)=\int_{\mathrm{1}} ^{{e}} \:\:\frac{\mathrm{2}}{\left(\mathrm{1}+{x}\right){u}\:+\left(\mathrm{1}−{x}\right){u}^{−\mathrm{1}} }\frac{{du}}{{u}} \\ $$$$=\int_{\mathrm{1}} ^{{e}} \:\:\:\frac{\mathrm{2}{du}}{\left(\mathrm{1}+{x}\right){u}^{\mathrm{2}} +\left(\mathrm{1}−{x}\right)}\:=\frac{\mathrm{2}}{\mathrm{1}+{x}}\:\int_{\mathrm{1}} ^{{e}} \:\frac{{du}}{{u}^{\mathrm{2}} \:+\frac{\mathrm{1}−{x}}{\mathrm{1}+{x}}} \\ $$$${case}\:\mathrm{1}\:\:\frac{\mathrm{1}−{x}}{\mathrm{1}+{x}}>\mathrm{0}\:\Rightarrow\mid{x}\mid<\mathrm{1}\:\:\:{we}\:{do}\:{the}\:{changement}\:{u}=\sqrt{\frac{\mathrm{1}−{x}}{\mathrm{1}+{x}}}{z}\:\Rightarrow \\ $$$${f}\left({x}\right)\:=\frac{\mathrm{2}}{\mathrm{1}+{x}}\:\int_{\sqrt{\frac{\mathrm{1}+{x}}{\mathrm{1}−{x}}}} ^{{e}\sqrt{\frac{\mathrm{1}+{x}}{\mathrm{1}−{x}}}} \:\:\:\:\frac{\mathrm{1}+{x}}{\mathrm{1}−{x}}\:\frac{\mathrm{1}}{\mathrm{1}+{z}^{\mathrm{2}} }\:\sqrt{\frac{\mathrm{1}−{x}}{\mathrm{1}+{x}}}{dz} \\ $$$$=\frac{\mathrm{2}}{\mathrm{1}−{x}}\frac{\sqrt{\mathrm{1}−{x}}}{\:\sqrt{\mathrm{1}+{x}}}\:\left[{arctan}\left({z}\right)\right]_{\sqrt{\frac{\mathrm{1}+{x}}{\mathrm{1}−{x}}}} ^{{e}\sqrt{\frac{\mathrm{1}+{x}}{\mathrm{1}−{x}}}} \\ $$$$=\frac{\mathrm{2}}{\:\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }}\left\{\:{arctan}\left({e}\sqrt{\frac{\mathrm{1}+{x}}{\mathrm{1}−{x}}}\right)−{arctan}\left(\sqrt{\frac{\mathrm{1}+{x}}{\mathrm{1}−{x}}}\right)\right\} \\ $$$${case}\:\mathrm{2}\:\:\frac{\mathrm{1}−{x}}{\mathrm{1}−{x}}<\mathrm{0}\:\Rightarrow\mid{x}\mid>\mathrm{1}\:\Rightarrow{f}\left({x}\right)=\frac{\mathrm{2}}{{x}+\mathrm{1}}\:\int_{\mathrm{1}} ^{{e}} \:\:\frac{{du}}{{u}^{\mathrm{2}} −\left(\sqrt{\frac{{x}−\mathrm{1}}{{x}+\mathrm{1}}}\right)^{\mathrm{2}} } \\ $$$$=_{{u}=\sqrt{\frac{{x}−\mathrm{1}}{{x}+\mathrm{1}}}{z}} \:\:\:\:\frac{\mathrm{2}}{{x}+\mathrm{1}}\:\int_{\sqrt{\frac{{x}+\mathrm{1}}{{x}−\mathrm{1}}}} ^{{e}\sqrt{\frac{{x}+\mathrm{1}}{{x}−\mathrm{1}}}} \:\:\:\:\frac{{x}+\mathrm{1}}{{x}−\mathrm{1}}\:\frac{\mathrm{1}}{{z}^{\mathrm{2}} −\mathrm{1}}\sqrt{\frac{{x}−\mathrm{1}}{{x}+\mathrm{1}}}{dz} \\ $$$$=\frac{\mathrm{1}}{{x}−\mathrm{1}}\frac{\sqrt{{x}−\mathrm{1}}}{\:\sqrt{{x}+\mathrm{1}}}\:\int_{\sqrt{\frac{{x}+\mathrm{1}}{{x}−\mathrm{1}}}} ^{{e}\sqrt{\frac{{x}+\mathrm{1}}{{x}−\mathrm{1}}}} \:\:\:\:\left\{\frac{\mathrm{1}}{{z}−\mathrm{1}}−\frac{\mathrm{1}}{{z}+\mathrm{1}}\right\}{dz} \\ $$$$=\frac{\mathrm{1}}{\:\sqrt{{x}^{\mathrm{2}} −\mathrm{1}}}\left[{ln}\mid\frac{{z}−\mathrm{1}}{{z}+\mathrm{1}}\mid\right]_{\sqrt{\frac{{x}+\mathrm{1}}{{x}−\mathrm{1}}}} ^{{e}\sqrt{\frac{{x}+\mathrm{1}}{{x}−\mathrm{1}}}} \:\:\:=\frac{\mathrm{1}}{\:\sqrt{{x}^{\mathrm{2}} −\mathrm{1}}}\left\{{ln}\mid\frac{\frac{{e}\sqrt{{x}+\mathrm{1}}}{\:\sqrt{{x}−\mathrm{1}}}−\mathrm{1}}{\frac{{e}\sqrt{{x}+\mathrm{1}}}{\:\sqrt{{x}−\mathrm{1}}}+\mathrm{1}}\mid\right. \\ $$$$\left.−{ln}\mid\frac{\frac{\sqrt{{x}+\mathrm{1}}}{\:\sqrt{{x}−\mathrm{1}}}−\mathrm{1}}{\frac{\sqrt{{x}+\mathrm{1}}}{\:\sqrt{{x}−\mathrm{1}}}+\mathrm{1}}\mid\right\}\:\Rightarrow \\ $$$${f}\left({x}\right)=\frac{\mathrm{1}}{\:\sqrt{{x}^{\mathrm{2}} −\mathrm{1}}}\left\{{ln}\mid\frac{{e}\sqrt{{x}+\mathrm{1}}−\sqrt{{x}−\mathrm{1}}}{{e}\sqrt{{x}+\mathrm{1}}+\sqrt{{x}−\mathrm{1}}}\mid−{ln}\mid\frac{\sqrt{{x}+\mathrm{1}}−\sqrt{{x}−\mathrm{1}}}{\:\sqrt{{x}+\mathrm{1}}+\sqrt{{x}−\mathrm{1}}}\mid\right\} \\ $$
Commented by mathmax by abdo last updated on 11/Aug/19
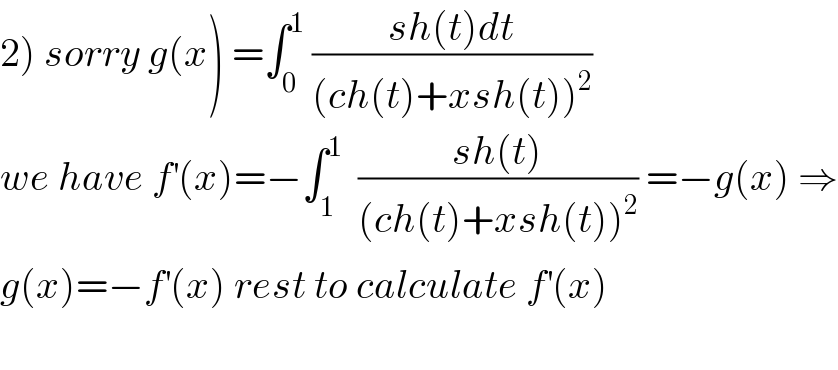
$$\left.\mathrm{2}\right)\:{sorry}\:{g}\left({x}\right)\:=\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{{sh}\left({t}\right){dt}}{\left({ch}\left({t}\right)+{xsh}\left({t}\right)\right)^{\mathrm{2}} } \\ $$$${we}\:{have}\:{f}^{'} \left({x}\right)=−\int_{\mathrm{1}} ^{\mathrm{1}} \:\:\frac{{sh}\left({t}\right)}{\left({ch}\left({t}\right)+{xsh}\left({t}\right)\right)^{\mathrm{2}} }\:=−{g}\left({x}\right)\:\Rightarrow \\ $$$${g}\left({x}\right)=−{f}^{'} \left({x}\right)\:{rest}\:{to}\:{calculate}\:{f}^{'} \left({x}\right) \\ $$$$ \\ $$
Commented by mathmax by abdo last updated on 11/Aug/19
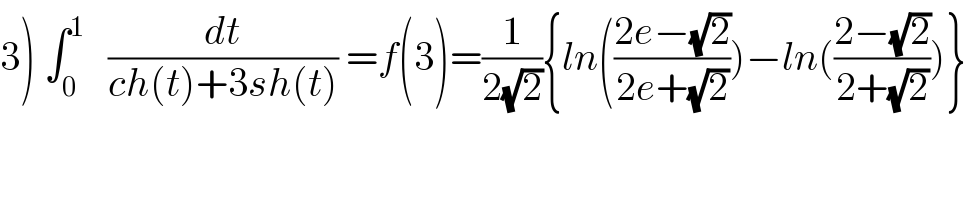
$$\left.\mathrm{3}\right)\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\:\frac{{dt}}{{ch}\left({t}\right)+\mathrm{3}{sh}\left({t}\right)}\:={f}\left(\mathrm{3}\right)=\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{2}}}\left\{{ln}\left(\frac{\mathrm{2}{e}−\sqrt{\mathrm{2}}}{\mathrm{2}{e}+\sqrt{\mathrm{2}}}\right)−{ln}\left(\frac{\mathrm{2}−\sqrt{\mathrm{2}}}{\mathrm{2}+\sqrt{\mathrm{2}}}\right)\right\} \\ $$
