Question Number 131836 by liberty last updated on 09/Feb/21
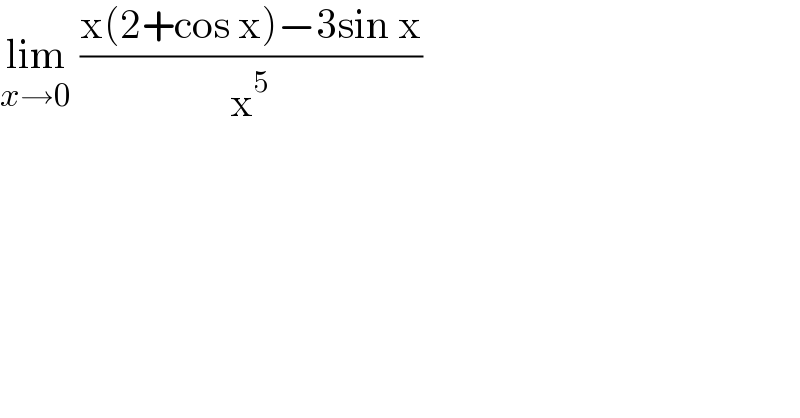
$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{x}\left(\mathrm{2}+\mathrm{cos}\:\mathrm{x}\right)−\mathrm{3sin}\:\mathrm{x}}{\mathrm{x}^{\mathrm{5}} } \\ $$
Commented by EDWIN88 last updated on 10/Feb/21
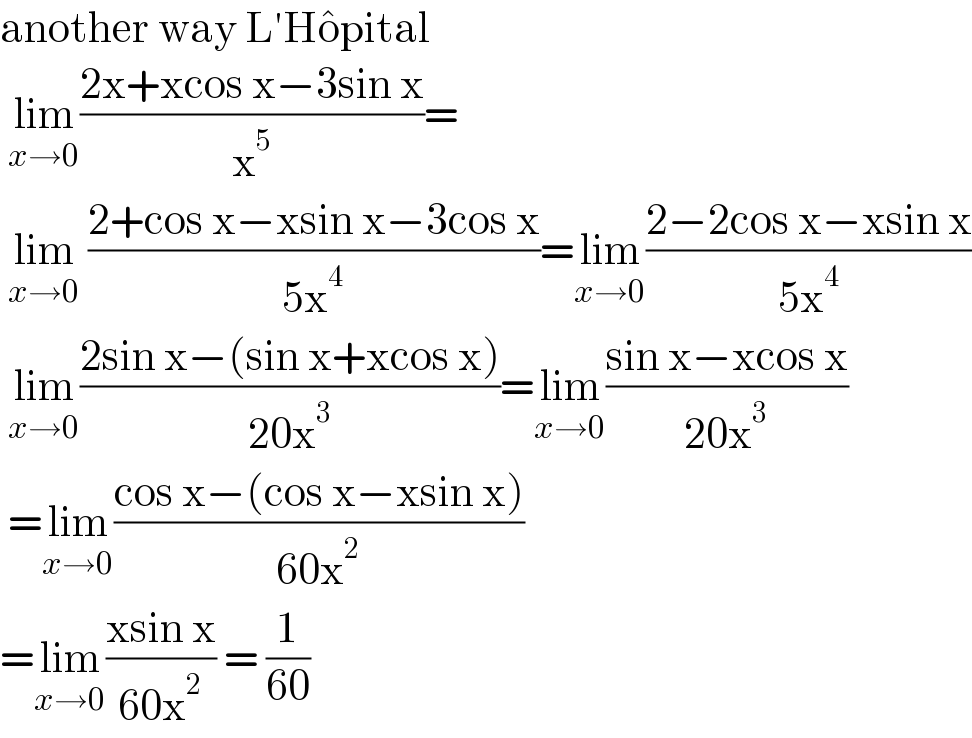
$$\mathrm{another}\:\mathrm{way}\:\mathrm{L}'\mathrm{H}\hat {\mathrm{o}pital} \\ $$$$\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{2x}+\mathrm{xcos}\:\mathrm{x}−\mathrm{3sin}\:\mathrm{x}}{\mathrm{x}^{\mathrm{5}} }= \\ $$$$\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{2}+\mathrm{cos}\:\mathrm{x}−\mathrm{xsin}\:\mathrm{x}−\mathrm{3cos}\:\mathrm{x}}{\mathrm{5x}^{\mathrm{4}} }=\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{2}−\mathrm{2cos}\:\mathrm{x}−\mathrm{xsin}\:\mathrm{x}}{\mathrm{5x}^{\mathrm{4}} } \\ $$$$\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{2sin}\:\mathrm{x}−\left(\mathrm{sin}\:\mathrm{x}+\mathrm{xcos}\:\mathrm{x}\right)}{\mathrm{20x}^{\mathrm{3}} }=\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{sin}\:\mathrm{x}−\mathrm{xcos}\:\mathrm{x}}{\mathrm{20x}^{\mathrm{3}} } \\ $$$$\:=\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{cos}\:\mathrm{x}−\left(\mathrm{cos}\:\mathrm{x}−\mathrm{xsin}\:\mathrm{x}\right)}{\mathrm{60x}^{\mathrm{2}} } \\ $$$$=\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{xsin}\:\mathrm{x}}{\mathrm{60x}^{\mathrm{2}} }\:=\:\frac{\mathrm{1}}{\mathrm{60}} \\ $$
Answered by EDWIN88 last updated on 10/Feb/21
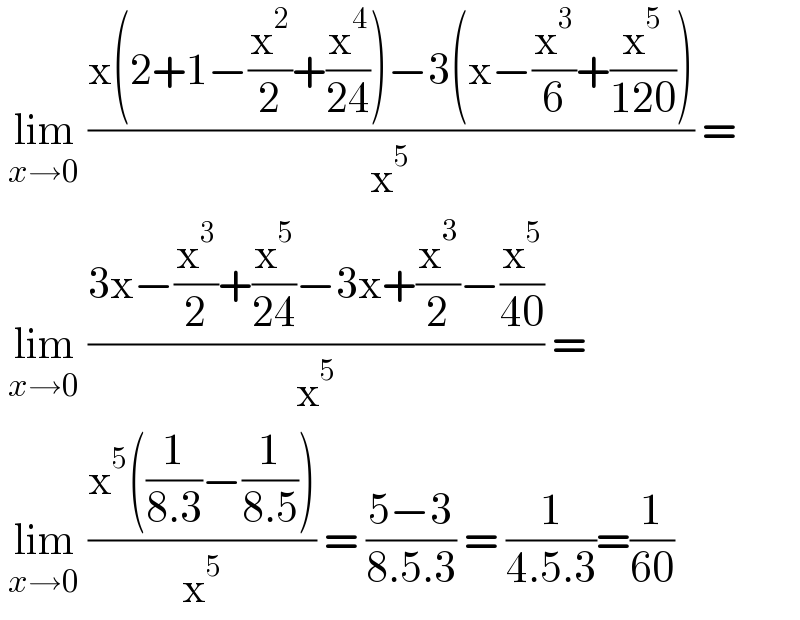
$$\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{x}\left(\mathrm{2}+\mathrm{1}−\frac{\mathrm{x}^{\mathrm{2}} }{\mathrm{2}}+\frac{\mathrm{x}^{\mathrm{4}} }{\mathrm{24}}\right)−\mathrm{3}\left(\mathrm{x}−\frac{\mathrm{x}^{\mathrm{3}} }{\mathrm{6}}+\frac{\mathrm{x}^{\mathrm{5}} }{\mathrm{120}}\right)}{\mathrm{x}^{\mathrm{5}} }\:= \\ $$$$\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{3x}−\frac{\mathrm{x}^{\mathrm{3}} }{\mathrm{2}}+\frac{\mathrm{x}^{\mathrm{5}} }{\mathrm{24}}−\mathrm{3x}+\frac{\mathrm{x}^{\mathrm{3}} }{\mathrm{2}}−\frac{\mathrm{x}^{\mathrm{5}} }{\mathrm{40}}}{\mathrm{x}^{\mathrm{5}} }\:= \\ $$$$\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{x}^{\mathrm{5}} \left(\frac{\mathrm{1}}{\mathrm{8}.\mathrm{3}}−\frac{\mathrm{1}}{\mathrm{8}.\mathrm{5}}\right)}{\mathrm{x}^{\mathrm{5}} }\:=\:\frac{\mathrm{5}−\mathrm{3}}{\mathrm{8}.\mathrm{5}.\mathrm{3}}\:=\:\frac{\mathrm{1}}{\mathrm{4}.\mathrm{5}.\mathrm{3}}=\frac{\mathrm{1}}{\mathrm{60}} \\ $$
Commented by malwan last updated on 10/Feb/21

$${thank}\:{you}\:{sir} \\ $$
Answered by malwan last updated on 09/Feb/21
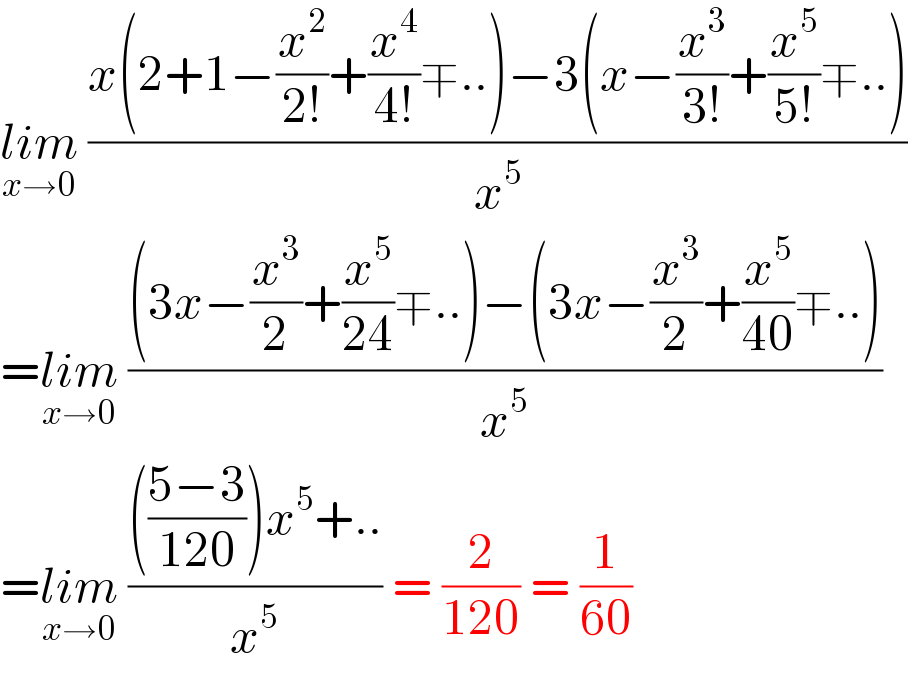
$$\underset{{x}\rightarrow\mathrm{0}} {{lim}}\:\frac{{x}\left(\mathrm{2}+\mathrm{1}−\frac{{x}^{\mathrm{2}} }{\mathrm{2}!}+\frac{{x}^{\mathrm{4}} }{\mathrm{4}!}\mp..\right)−\mathrm{3}\left({x}−\frac{{x}^{\mathrm{3}} }{\mathrm{3}!}+\frac{{x}^{\mathrm{5}} }{\mathrm{5}!}\mp..\right)}{{x}^{\mathrm{5}} } \\ $$$$=\underset{{x}\rightarrow\mathrm{0}} {{lim}}\:\frac{\left(\mathrm{3}{x}−\frac{{x}^{\mathrm{3}} }{\mathrm{2}}+\frac{{x}^{\mathrm{5}} }{\mathrm{24}}\mp..\right)−\left(\mathrm{3}{x}−\frac{{x}^{\mathrm{3}} }{\mathrm{2}}+\frac{{x}^{\mathrm{5}} }{\mathrm{40}}\mp..\right)}{{x}^{\mathrm{5}} } \\ $$$$=\underset{{x}\rightarrow\mathrm{0}} {{lim}}\:\frac{\left(\frac{\mathrm{5}−\mathrm{3}}{\mathrm{120}}\right){x}^{\mathrm{5}} +..}{{x}^{\mathrm{5}} }\:=\:\frac{\mathrm{2}}{\mathrm{120}}\:=\:\frac{\mathrm{1}}{\mathrm{60}} \\ $$
