Menu Close

Prove-by-contradiction-that-there-are-no-whole-number-solutions-x-y-z-to-the-equation-z-2-x-2-y-2-where-both-x-and-y-are-odd-

Tinku Tara 0 Comments
Pin




Question Number 2655 by Yozzi last updated on 24/Nov/15
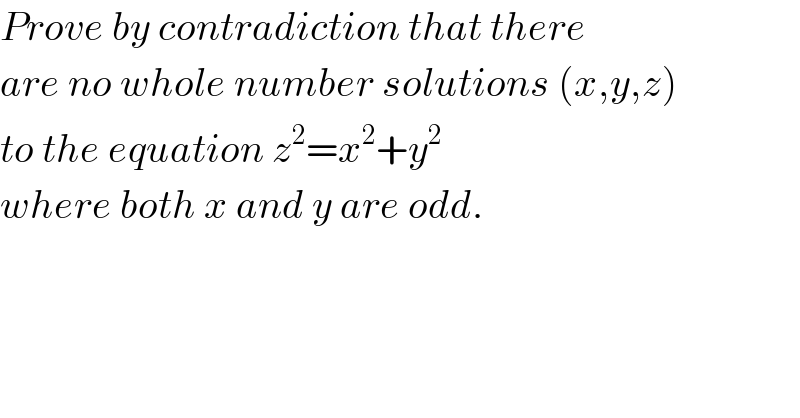
Prove by contradiction that there are no whole number solutions (x,y,z) to the equation z^2 =x^2 +y^2 where both x and y are odd.
$${Prove}\:{by}\:{contradiction}\:{that}\:{there} \\ $$$${are}\:{no}\:{whole}\:{number}\:{solutions}\:\left({x},{y},{z}\right) \\ $$$${to}\:{the}\:{equation}\:{z}^{\mathrm{2}} ={x}^{\mathrm{2}} +{y}^{\mathrm{2}} \\ $$$${where}\:{both}\:{x}\:{and}\:{y}\:{are}\:{odd}. \\ $$
Answered by prakash jain last updated on 24/Nov/15
Let us assume that such a solution exists j,k,l∈N∪{0} x=2k+1 y=2j+1 since x,y are odd z must be even z=2l z^2 =x^2 +y^2 4l^2 =4k^2 +4k+1+4j^2 +4j+1 l^2 =k^2 +k+j^2 +j+(1/2) l^2 is a fraction. Contradicts that z is a whole number or l is a whole number.
$$\mathrm{Let}\:\mathrm{us}\:\mathrm{assume}\:\mathrm{that}\:\mathrm{such}\:\mathrm{a}\:\mathrm{solution}\:\mathrm{exists} \\ $$$${j},{k},{l}\in\mathbb{N}\cup\left\{\mathrm{0}\right\} \\ $$$${x}=\mathrm{2}{k}+\mathrm{1} \\ $$$${y}=\mathrm{2}{j}+\mathrm{1} \\ $$$$\mathrm{since}\:{x},{y}\:{are}\:{odd}\:{z}\:{must}\:{be}\:{even} \\ $$$${z}=\mathrm{2}{l} \\ $$$${z}^{\mathrm{2}} ={x}^{\mathrm{2}} +{y}^{\mathrm{2}} \\ $$$$\mathrm{4}{l}^{\mathrm{2}} =\mathrm{4}{k}^{\mathrm{2}} +\mathrm{4}{k}+\mathrm{1}+\mathrm{4}{j}^{\mathrm{2}} +\mathrm{4}{j}+\mathrm{1} \\ $$$${l}^{\mathrm{2}} ={k}^{\mathrm{2}} +{k}+{j}^{\mathrm{2}} +{j}+\frac{\mathrm{1}}{\mathrm{2}} \\ $$$${l}^{\mathrm{2}} \:\mathrm{is}\:\mathrm{a}\:\mathrm{fraction}.\:\mathrm{Contradicts}\:\mathrm{that}\:{z}\:\mathrm{is}\:\mathrm{a}\:\mathrm{whole} \\ $$$$\mathrm{number}\:\mathrm{or}\:{l}\:\mathrm{is}\:\mathrm{a}\:\mathrm{whole}\:\mathrm{number}. \\ $$
Commented by Rasheed Soomro last updated on 24/Nov/15
Inspiring!
$$\mathcal{I}{nspiring}! \\ $$
Answered by Filup last updated on 24/Nov/15
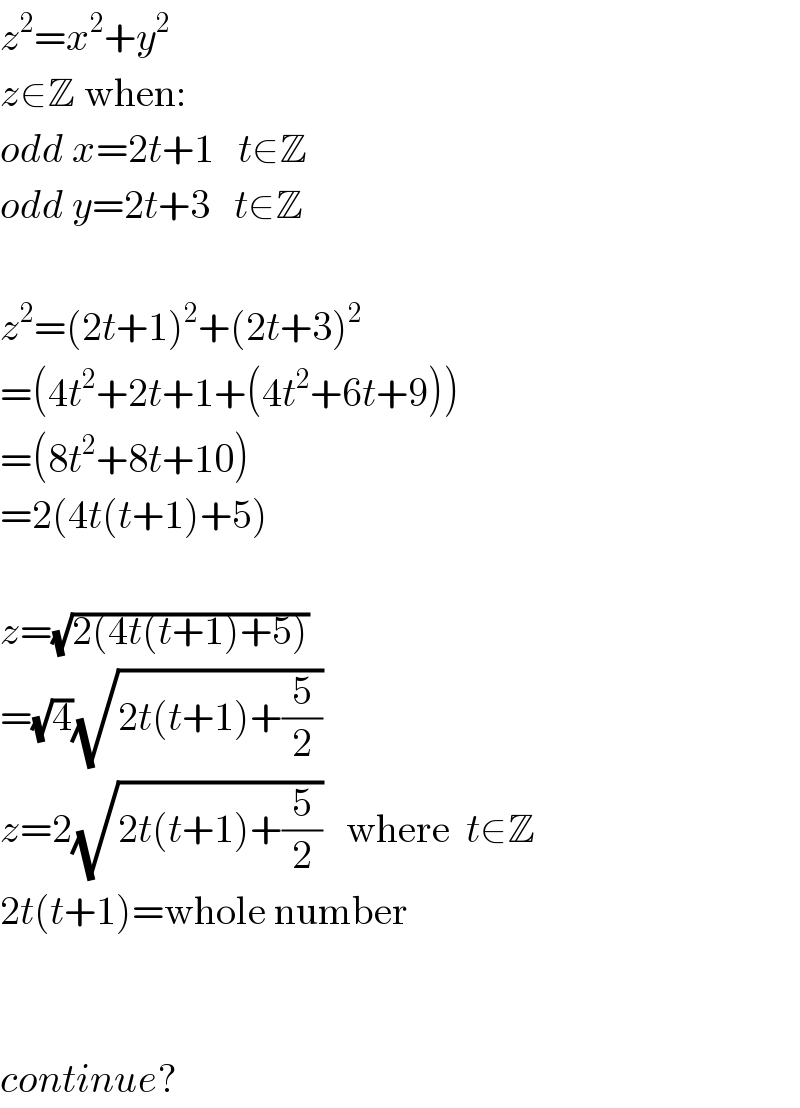
z^2 =x^2 +y^2 z∈Z when: odd x=2t+1 t∈Z odd y=2t+3 t∈Z z^2 =(2t+1)^2 +(2t+3)^2 =(4t^2 +2t+1+(4t^2 +6t+9)) =(8t^2 +8t+10) =2(4t(t+1)+5) z=(√(2(4t(t+1)+5))) =(√4)(√(2t(t+1)+(5/2))) z=2(√(2t(t+1)+(5/2))) where t∈Z 2t(t+1)=whole number continue?
$${z}^{\mathrm{2}} ={x}^{\mathrm{2}} +{y}^{\mathrm{2}} \\ $$$${z}\in\mathbb{Z}\:\mathrm{when}: \\ $$$${odd}\:{x}=\mathrm{2}{t}+\mathrm{1}\:\:\:{t}\in\mathbb{Z} \\ $$$${odd}\:{y}=\mathrm{2}{t}+\mathrm{3}\:\:\:{t}\in\mathbb{Z} \\ $$$$ \\ $$$${z}^{\mathrm{2}} =\left(\mathrm{2}{t}+\mathrm{1}\right)^{\mathrm{2}} +\left(\mathrm{2}{t}+\mathrm{3}\right)^{\mathrm{2}} \\ $$$$=\left(\mathrm{4}{t}^{\mathrm{2}} +\mathrm{2}{t}+\mathrm{1}+\left(\mathrm{4}{t}^{\mathrm{2}} +\mathrm{6}{t}+\mathrm{9}\right)\right) \\ $$$$=\left(\mathrm{8}{t}^{\mathrm{2}} +\mathrm{8}{t}+\mathrm{10}\right) \\ $$$$=\mathrm{2}\left(\mathrm{4}{t}\left({t}+\mathrm{1}\right)+\mathrm{5}\right) \\ $$$$ \\ $$$${z}=\sqrt{\mathrm{2}\left(\mathrm{4}{t}\left({t}+\mathrm{1}\right)+\mathrm{5}\right)} \\ $$$$=\sqrt{\mathrm{4}}\sqrt{\mathrm{2}{t}\left({t}+\mathrm{1}\right)+\frac{\mathrm{5}}{\mathrm{2}}} \\ $$$${z}=\mathrm{2}\sqrt{\mathrm{2}{t}\left({t}+\mathrm{1}\right)+\frac{\mathrm{5}}{\mathrm{2}}}\:\:\:\mathrm{where}\:\:{t}\in\mathbb{Z} \\ $$$$\mathrm{2}{t}\left({t}+\mathrm{1}\right)=\mathrm{whole}\:\mathrm{number} \\ $$$$ \\ $$$$ \\ $$$${continue}? \\ $$
Commented by Filup last updated on 24/Nov/15
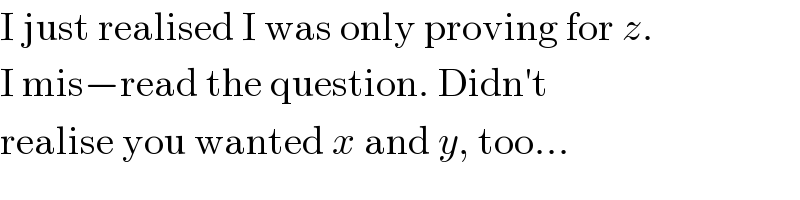
I just realised I was only proving for z. I mis−read the question. Didn′t realise you wanted x and y, too...
$$\mathrm{I}\:\mathrm{just}\:\mathrm{realised}\:\mathrm{I}\:\mathrm{was}\:\mathrm{only}\:\mathrm{proving}\:\mathrm{for}\:{z}. \\ $$$$\mathrm{I}\:\mathrm{mis}−\mathrm{read}\:\mathrm{the}\:\mathrm{question}.\:\mathrm{Didn}'\mathrm{t} \\ $$$$\mathrm{realise}\:\mathrm{you}\:\mathrm{wanted}\:{x}\:\mathrm{and}\:{y},\:\mathrm{too}… \\ $$
Commented by prakash jain last updated on 24/Nov/15
You started with x=2t+1 and y=2t+3 the question only said x and y are odd and did not state that x and y are consecutive odd numbers. The last part of your conclusion z=2(√(2t(t+1)+(5/2))) is valid since you have a fraction under the root sign so you cannot get a whole number. Also proving for z is sufficient as the question only requires to prove that condition on all 3 variables are not satisfied simultaneously. So proving by assuming 2 variables meet condition and creating a contradiction on 3rd is sufficient.
$$\mathrm{You}\:\mathrm{started}\:\mathrm{with}\:{x}=\mathrm{2}{t}+\mathrm{1}\:\mathrm{and}\:{y}=\mathrm{2}{t}+\mathrm{3} \\ $$$$\mathrm{the}\:\mathrm{question}\:\mathrm{only}\:\mathrm{said}\:{x}\:\mathrm{and}\:{y}\:\mathrm{are}\:\mathrm{odd}\:\mathrm{and} \\ $$$$\mathrm{did}\:\mathrm{not}\:\mathrm{state}\:\mathrm{that}\:{x}\:\mathrm{and}\:{y}\:\mathrm{are}\:\mathrm{consecutive} \\ $$$$\mathrm{odd}\:\mathrm{numbers}. \\ $$$$\mathrm{The}\:\mathrm{last}\:\mathrm{part}\:\mathrm{of}\:\mathrm{your}\:\mathrm{conclusion} \\ $$$${z}=\mathrm{2}\sqrt{\mathrm{2}{t}\left({t}+\mathrm{1}\right)+\frac{\mathrm{5}}{\mathrm{2}}}\:\:\mathrm{is}\:\mathrm{valid}\:\mathrm{since}\:\mathrm{you}\:\mathrm{have} \\ $$$$\mathrm{a}\:\mathrm{fraction}\:\mathrm{under}\:\mathrm{the}\:\mathrm{root}\:\mathrm{sign}\:\mathrm{so}\:\mathrm{you} \\ $$$$\mathrm{cannot}\:\mathrm{get}\:\mathrm{a}\:\mathrm{whole}\:\mathrm{number}. \\ $$$$\mathrm{Also}\:\mathrm{proving}\:\mathrm{for}\:{z}\:\mathrm{is}\:\mathrm{sufficient}\:\mathrm{as}\:\mathrm{the}\:\mathrm{question} \\ $$$$\mathrm{only}\:\mathrm{requires}\:\mathrm{to}\:\mathrm{prove}\:\mathrm{that}\:\mathrm{condition}\:\mathrm{on} \\ $$$$\mathrm{all}\:\mathrm{3}\:\mathrm{variables}\:\mathrm{are}\:\mathrm{not}\:\mathrm{satisfied}\:\mathrm{simultaneously}. \\ $$$$\mathrm{So}\:\mathrm{proving}\:\mathrm{by}\:\mathrm{assuming}\:\mathrm{2}\:\mathrm{variables}\:\mathrm{meet} \\ $$$$\mathrm{condition}\:\mathrm{and}\:\mathrm{creating}\:\mathrm{a}\:\mathrm{contradiction}\:\mathrm{on} \\ $$$$\mathrm{3rd}\:\mathrm{is}\:\mathrm{sufficient}. \\ $$
Commented by Filup last updated on 24/Nov/15
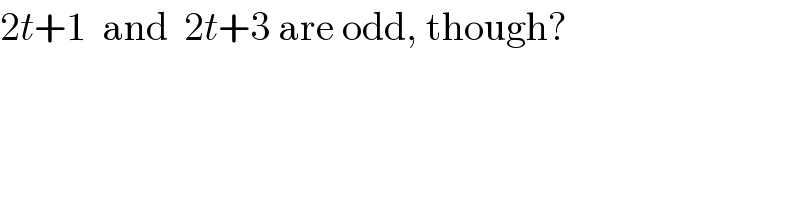
2t+1 and 2t+3 are odd, though?
$$\mathrm{2}{t}+\mathrm{1}\:\:\mathrm{and}\:\:\mathrm{2}{t}+\mathrm{3}\:\mathrm{are}\:\mathrm{odd},\:\mathrm{though}? \\ $$
Commented by prakash jain last updated on 24/Nov/15
Yes. But consecutive odd number. So the conditions are more restrictive than required by question.
$$\mathrm{Yes}.\:\mathrm{But}\:\mathrm{consecutive}\:\mathrm{odd}\:\mathrm{number}.\:\mathrm{So} \\ $$$$\mathrm{the}\:\mathrm{conditions}\:\mathrm{are}\:\mathrm{more}\:\mathrm{restrictive}\:\mathrm{than} \\ $$$$\mathrm{required}\:\mathrm{by}\:\mathrm{question}. \\ $$
Commented by Filup last updated on 25/Nov/15
I understand now
$$\mathrm{I}\:\mathrm{understand}\:\mathrm{now} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *