Question Number 3298 by prakash jain last updated on 09/Dec/15
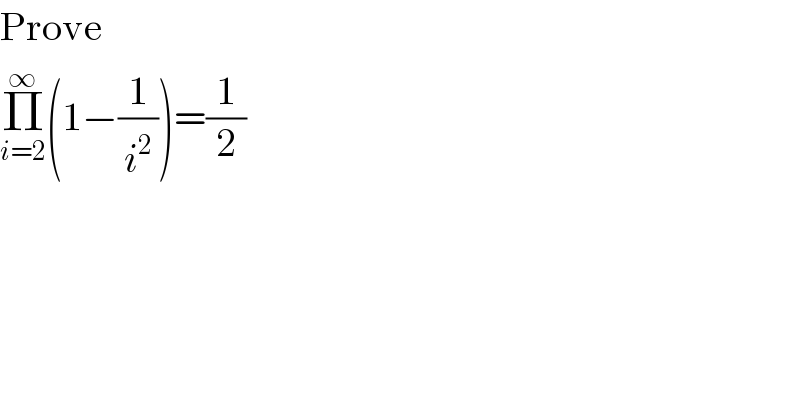
$$\mathrm{Prove} \\ $$$$\underset{{i}=\mathrm{2}} {\overset{\infty} {\prod}}\left(\mathrm{1}−\frac{\mathrm{1}}{{i}^{\mathrm{2}} }\right)=\frac{\mathrm{1}}{\mathrm{2}} \\ $$
Commented by 123456 last updated on 10/Dec/15
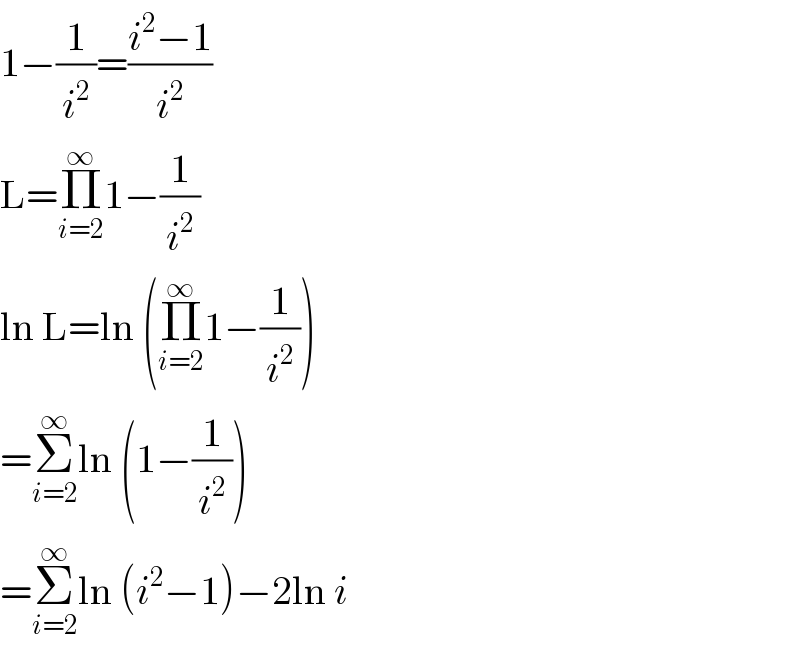
$$\mathrm{1}−\frac{\mathrm{1}}{{i}^{\mathrm{2}} }=\frac{{i}^{\mathrm{2}} −\mathrm{1}}{{i}^{\mathrm{2}} } \\ $$$$\mathrm{L}=\underset{{i}=\mathrm{2}} {\overset{\infty} {\prod}}\mathrm{1}−\frac{\mathrm{1}}{{i}^{\mathrm{2}} } \\ $$$$\mathrm{ln}\:\mathrm{L}=\mathrm{ln}\:\left(\underset{{i}=\mathrm{2}} {\overset{\infty} {\prod}}\mathrm{1}−\frac{\mathrm{1}}{{i}^{\mathrm{2}} }\right) \\ $$$$=\underset{{i}=\mathrm{2}} {\overset{\infty} {\sum}}\mathrm{ln}\:\left(\mathrm{1}−\frac{\mathrm{1}}{{i}^{\mathrm{2}} }\right) \\ $$$$=\underset{{i}=\mathrm{2}} {\overset{\infty} {\sum}}\mathrm{ln}\:\left({i}^{\mathrm{2}} −\mathrm{1}\right)−\mathrm{2ln}\:{i} \\ $$
Answered by prakash jain last updated on 10/Dec/15
![continuing with comment from 123456 ln L=Σ_(i=2) ^∞ (ln(i^2 −1)−2ln(i)) =Σ_(i=2 ) ^∞ [ln(i−1)+ln (i+1)−2ln(i)] This is telescoping sum. ln L=−ln 2](https://www.tinkutara.com/question/Q3310.png)
$$\mathrm{continuing}\:\mathrm{with}\:\mathrm{comment}\:\mathrm{from}\:\mathrm{123456} \\ $$$$\mathrm{ln}\:\mathrm{L}=\underset{{i}=\mathrm{2}} {\overset{\infty} {\sum}}\left(\mathrm{ln}\left({i}^{\mathrm{2}} −\mathrm{1}\right)−\mathrm{2}{ln}\left({i}\right)\right) \\ $$$$=\underset{{i}=\mathrm{2}\:} {\overset{\infty} {\sum}}\left[\mathrm{ln}\left(\mathrm{i}−\mathrm{1}\right)+\mathrm{ln}\:\left(\mathrm{i}+\mathrm{1}\right)−\mathrm{2ln}\left(\mathrm{i}\right)\right] \\ $$$$\mathrm{This}\:\mathrm{is}\:\mathrm{telescoping}\:\mathrm{sum}. \\ $$$$\mathrm{ln}\:\mathrm{L}=−\mathrm{ln}\:\mathrm{2} \\ $$
Commented by prakash jain last updated on 10/Dec/15
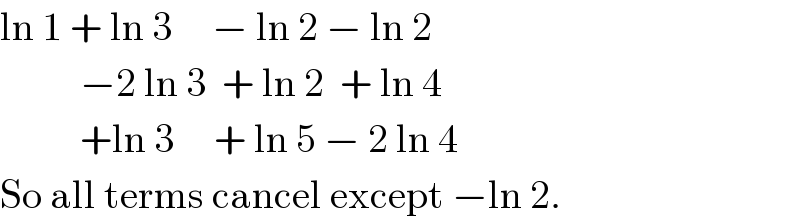
$$\mathrm{ln}\:\mathrm{1}\:+\:\mathrm{ln}\:\mathrm{3}\:\:\:\:\:−\:\mathrm{ln}\:\mathrm{2}\:−\:\mathrm{ln}\:\mathrm{2}\:\:\: \\ $$$$\:\:\:\:\:\:\:\:\:\:−\mathrm{2}\:\mathrm{ln}\:\mathrm{3}\:\:+\:\mathrm{ln}\:\mathrm{2}\:\:+\:\mathrm{ln}\:\mathrm{4} \\ $$$$\:\:\:\:\:\:\:\:\:\:+\mathrm{ln}\:\mathrm{3}\:\:\:\:\:+\:\mathrm{ln}\:\mathrm{5}\:−\:\mathrm{2}\:\mathrm{ln}\:\mathrm{4} \\ $$$$\mathrm{So}\:\mathrm{all}\:\mathrm{terms}\:\mathrm{cancel}\:\mathrm{except}\:−\mathrm{ln}\:\mathrm{2}. \\ $$
