Question Number 133980 by mohammad17 last updated on 26/Feb/21
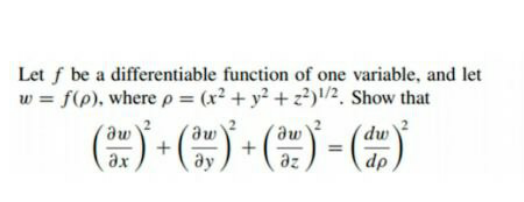
Answered by mr W last updated on 26/Feb/21

$$\frac{\partial{p}}{\partial{x}}=\frac{{x}}{\:\sqrt{{x}^{\mathrm{2}} +{y}^{\mathrm{2}} +{z}^{\mathrm{2}} }} \\ $$$$\frac{\partial{p}}{\partial{y}}=\frac{{y}}{\:\sqrt{{x}^{\mathrm{2}} +{y}^{\mathrm{2}} +{z}^{\mathrm{2}} }} \\ $$$$\frac{\partial{p}}{\partial{z}}=\frac{{z}}{\:\sqrt{{x}^{\mathrm{2}} +{y}^{\mathrm{2}} +{z}^{\mathrm{2}} }} \\ $$$$\frac{\partial{w}}{\partial{x}}=\frac{{dw}}{{dp}}×\frac{\partial{p}}{\partial{x}}=\frac{{dw}}{{dp}}×\frac{{x}}{\:\sqrt{{x}^{\mathrm{2}} +{y}^{\mathrm{2}} +{z}^{\mathrm{2}} }} \\ $$$$\left(\frac{\partial{w}}{\partial{x}}\overset{\mathrm{2}} {\right)}=\left(\frac{{dw}}{{dp}}\right)^{\mathrm{2}} ×\frac{{x}^{\mathrm{2}} }{\:{x}^{\mathrm{2}} +{y}^{\mathrm{2}} +{z}^{\mathrm{2}} } \\ $$$$\left(\frac{\partial{w}}{\partial{y}}\overset{\mathrm{2}} {\right)}=\left(\frac{{dw}}{{dp}}\right)^{\mathrm{2}} ×\frac{{y}^{\mathrm{2}} }{\:{x}^{\mathrm{2}} +{y}^{\mathrm{2}} +{z}^{\mathrm{2}} } \\ $$$$\left(\frac{\partial{w}}{\partial{z}}\overset{\mathrm{2}} {\right)}=\left(\frac{{dw}}{{dp}}\right)^{\mathrm{2}} ×\frac{{z}^{\mathrm{2}} }{\:{x}^{\mathrm{2}} +{y}^{\mathrm{2}} +{z}^{\mathrm{2}} } \\ $$$$\Rightarrow\left(\frac{\partial{w}}{\partial{x}}\overset{\mathrm{2}} {\right)}+\left(\frac{\partial{w}}{\partial{y}}\overset{\mathrm{2}} {\right)}+\left(\frac{\partial{w}}{\partial{z}}\overset{\mathrm{2}} {\right)}=\left(\frac{{dw}}{{dp}}\overset{\mathrm{2}} {\right)} \\ $$
